Gästinlägg av docenten, meteorologen och klimatologen Tage Andersson
Här på TCS diskuteras och missförstås ofta trender. Vad är då en trend? Vad gäller tid är det en tendens eller utveckling av något som man söker sammanfatta och åskådligt beskriva. Ofta för att få veta något om framtiden. En förhoppning som i regel gäckas. För att man ska kunna tolka en trend måste den vara enkel, som en rät linje. Komplicerade kurvor klarar man inte, och vad värre är, de spårar ofta ur med katastrofala resultat som följd.
Jag ska illustrera trender med hjälp av tidsserien från CRU (Climatic Research Unit i England) som ger årsvärden av den globala medeltemperaturen nära jordytan perioden 1850-2010. (hämtad 110831)
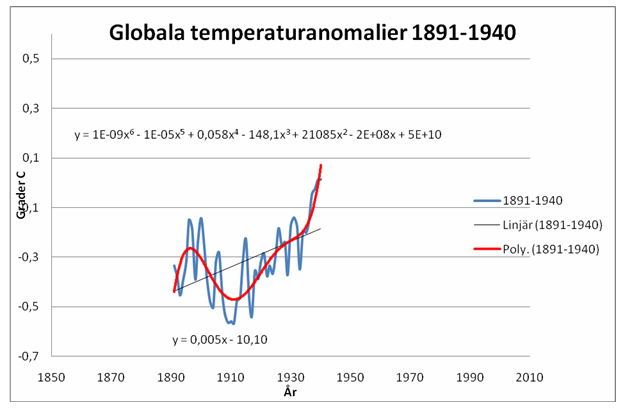
För att illustrera trendernas tidsberoende väljer vi ut 50-årsperioden 1891-1940, se fig 1. Vi anpassar, med minsta kvadratmetoden, en rät linje till observationerna. Minsta kvadratmetoden innebär att vi beräknar skillnaden mellan en tänkbar rät linjes värde och observationens värde och multiplicerar det med sig själv. Den produkten beräknar vi för alla observationer. Därefter summerar vi dessa produkter och väljer den räta linje som får minsta summan. Då anser vi oss ha fått bästa möjliga räta linje-approximation. Den svarta linjen i fig 1 visar resultatet. Det kanske inte är så tokigt men vi kan nog få bättre anpassning om vi söker en kurva. Så låt oss söka en sådan.
Den räta linjen har ekvationen
Y=k*x+L
För en kurva väljer vi en 6-gradsekvation/polynom/
Y=k1*x+k2*x2+k3*x3+k4*x4+k5*x5+k6*x6+L
Det är krångligt, men dagens PC klarar det utan vidare.
Den röda kurvan visar att nu blir det bättre. Den ligger mycket närmare observationerna. Men den fina anpassningen har ett högt pris.
Fig 1. Observationer av den globala årsmedeltemperaturen perioden 1891-1940 (blå kurva) och anpassning till dem med rät linje (svart) och 6-graders/kurva/polynom (röd )
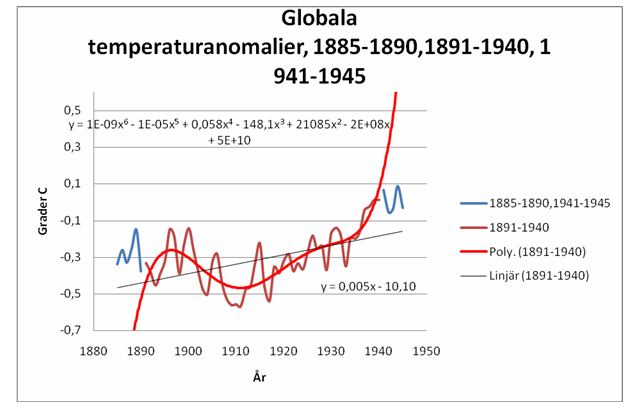
Vi ser att såväl i början som slutet är den röda kurvan väldigt brant. Det innebär att om vi låter den ge värden längre fram (efter 1940) eller tidigare (före 1891) går det väldigt dåligt, fig 2.
Fig 2. Observationer av den globala årsmedeltemperaturen perioden 1885-1945 (brun och blå kurva ) och anpassning till dem med rät linje (svart) och 6-graders/kurva/polynom (röd). Anpassningarna utförda för perioden 1891-1940. Observera att den röda kurvan spårar ur katastrofalt utanför 1891-1940. Observera också att det är annan x-skala än i fig1 .
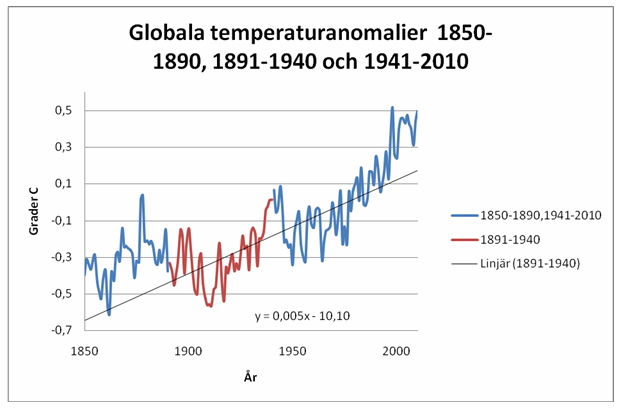
Redan ett par år efter eller före perioden 1891-1940 spårar den röda kurvan fullständigt ur och den enkla räta linjen passar observationerna bättre. Hur det blir om vi ser på hela perioden 1850-2010 kan vi förstås tänka oss, men för säkerhets skull visas det i fig 3.
Fig 3. Observationer av den globala årsmedeltemperaturen perioden 1850-2010(brun och blå kurva ) och anpassning till dem med rät linje (svart). Anpassningen utförd för perioden 1891-1940. 6-graderskurvan ryms inte inom y-skalan, m.a.o. ger fullständigt vansinniga värden utanför intervallet 1891-1940.
Den röda kurvan saknas, helt enkelt eftersom den rusar ut ur figuren, såväl före 1890 som efter 1940. Detta illustrerar en viktig princip. Rent matematiskt kan man få väldigt bra anpassning till kända data, bara genom att anpassa dem till en lämplig funktion. Men sannolikt funkar det inte utanför det valdaintervallet, här utanför tidsintervallet 1891-1940. Om vi går vi utanför det blir resultatet katastrofalt för den röda 6e-gradskurvan. Den enkla räta linjen lyckas mycket bättre såväl före 1890 som efter 1940.
Detta resonemang gäller för alla samband som saknar fysikalisk eller annan vettig motivering. Tack vare våra PC är det numera enkelt att söka alla sorters samband och hitta till synes bra sådana, men deras prognostiska värde är obefintligt tills man visar att de gäller också för oberoende data, i detta fall data utanför anpassningsintervallet 1890-1940.
Vad klimatmodellerna anbelangar har de en klar fysikalisk motivering för CO2. Aerosolernas egenskaper är komplicerade och dåligt kända. Samma gäller moln och nederbörd. Kosmiska influenser kan inte tas med, eftersom de f.n. inte kan kvantiseras. Därför kan man inte hävda att klimatmodellerna bygger på känd fysik. Eftersom det saknas oberoende data att testa dem mot är de icke verifierade och deras prognosförmåga okänd, sannolikt mycket låg.








Polynom visar inte tender utanför observationerna, den skär punkterna om du har punkter +1 som n. Det kan vara bra om man vill uppskatta ett värde mellan två punkter annars inte.
Enda ställe jag känner till som regelbundet försöker sig på med anpassning via högre graders polynom är climate4you som brukar länkas till flitigt här.
Intressant inside information. Kurvpassning (curv fitting) är kända metoder för att få snygga kurvor i rapporter, men detta gäller anpassning till kända data. Tage visar ju här att denna metod inte är användbar för data utanför dataserien, men ändå bygger hela klimatmodelleringen på fiktiva dataserier. Eftersom klimatframtiden är okänd, måste dessa prognoser som IPCC saluför, vara bedrägligt lurendrejeri.
Thomas #2
Jo jag hittade en sådan graf. Den illustrerar ett cyklist fenomen. De försökt inte använda den för att extrapolera framtiden. Det var väl det som artikeln ovan argumenterade mot?
Till och börja med så kan man väl säga att det är bra att matematik-metodiken diskuteras då det är uppenbart att väldigt många har problem med sådant.
Vad gäller artikelförfattarens teorier så är ”modell ansatsen” både vetenskapligt och matematiskt förkastad som en grund för teoribyggnad. Rent matematiskt exempelvis så finns det alltid en oändlig mängd modeller (andra förklaringar) som kan passa ett datamaterial bättre än den föreslagna och därför kan man direkt förkasta alla förklaringar som baseras på polynom-ekvationer, räta linjen, generaliserande linjära modeller, tidsserieanalys, beslutsteori eller vilket poppisnamn man nu försett den föreslagna teorin med.
Vidare är det alltid som så att data som samlats in, samlats in antingen i en experimentell process eller genom ett samplingförfarande. Vad gäller samplingförfarande så föreskriver matematiken för lägsta nivån av giltighet att samplingsförfarandet genomförts, vilket i praktiken är helt omöjligt. Vad gäller de experimentella processerna så är det matematiskt motbevisade (design av experiment, försök ”vilket nytt poppis namn de försetts med” osv.) och utövaren måste helt förlita sig på att experimentet kan upprepas för att det över huvudtaget skall finnas någon anledning att ta resultaten i beaktande.
Så även artikelförfattaren behöver nog förbättra sin kompetens en smula.
Anonym.
Och den där sista lilla kängan? Var den verkligen nödvändig??
ANNONym xxx [5]; Om jag har förstått dig rätt, är det en omöjlighet att matematiskt förutsäga klimatutvecklingen eftersom denna process inte går att upprepa. Klimatet är alltså inte på något sätt verifierbart, med andra ord oförutsägbart.
Re Ingvar: Förlåt, jag ber om ursäkt men det är trots allt nödvändigt att få upp nivån en smula angående just det här så att man inte hamnar i situationen av ett ”en historia som upprepar sig”. Artikelförfattaren är givetvis välkommen att skriva en fördjupad artikel i ämnet då det inte är svårare än bingo och poker matematik, efter att man exorcerat hieroglyferna.
Re Björn: Med dagens vetenskapliga nivå på mätningar så behövs ingen matematik för att förutsäga klimatet då mätningarna är så dåliga att man kan komma till vilket resultat man så önskar. Vad gäller matematiken så finns det enbart sampling teorin för att förutspå klimatet och då är det i praktiken omöjligt att genomföra på ett tillfredsställande vis. Vidare skulle ”sampling felet” oaktat alla andra fel bli så stort att man inte skulle kunna detektera klimatförändringar av sorten E[klimat degrees C] mindre än säg +2C.
Vidare så verkar klimatet lokalt hektar-hektar variera så mycket att begreppet ”enskilda mätningar” kan betvivlas map. mätningarna. Man kan studera nederbörd i ökengränstrakter för att se sådant. Där har scamen en liten liten fördel i att ingen klagar som får större nederbörd, så länge marken kan absorbera nederbörden, men alla som får mindre nederbörd skriker (nåja, bönder i alla fall). Givetvis har den naturliga variationen alltid varit extremt stor i sådana områden.
Och ja, det är helt omöjligt att förutse klimatet med CRU, FN:s, SMHI:s eller liknande metoder, resurser, kompetens, förmåga osv.
Alltså dags att lagföra hela bedrägeriets alla utövare. Skönt att få det klarlagt, så kan vi ju lägga ner alla klimatbloggar i båda lägren.
Vi kan ju behålla fredagsmyset med roliga vitsar.
Tex:
– Väldigt vad mager den kanibalen är.
– Ja, han måste äta upp sig.
Bim, ja det är egentligen otroligt vilka pyramidala proportioner en ickefråga som CO2-hypotesen har fått! Medan vi försummar verkliga problem.
OT men klart läsvärt. Prof. William Happer inför en del av senaten:
http://epw.senate.gov/public/index.cfm?FuseAction=Files.View&FileStore_id=84462e2d-6bff-4983-a574-31f5ae8e8a42
ANNONym xxx
Om jag förstår dig rätt så är du kunnig på området.
Eftersom du föredrar att vara anonym så kanske ditt namn har viss signifikans.
Vad gör du för att försöka få till en ändring på vansinnespolitiken?
Ingvar #4, för det första är det inte något cykliskt fenomen om vi tittar på samma kurva. För det andra är polynom usla för att anpassa till cykliska fenomen.
Polynom av högre gradtal är inte ens bra för att interpolera. Givet X punkter kan man alltid hitta ett polynom av gradtal X-1 som passerar genom dem alla, men om X>3 så kommer polynomet ofta att ha vilda oscillationer mellan punkterna.
Thomas#13
Då får du peka på vilken graf du menar. De jag hittar på deras site tycker jag illudtrerar ett cyklist fenomen ganska bra.
http://www.theonion.com/video/nations-climatologists-exhibiting-strange-behavior,21009/
Vi har blivit förda bakom ljuset och inbillats att man kan ”räkna ut” klimatframtiden. Det är lika dumt som determinister som tror att om man vid ett visst tillfälle kände till alla atomers lägen, skulle man kunna räkna ut och förutsäga universums utveckling. Det finns en naiv övertro på matematikens möjligheter. Det bör stå klart för varje individ, att det är omöjligt att förutsäga framtiden med matematik. Framtiden är inte kalkylerbar. När skall vi få beslutsfattare som begriper detta och handlar därefter?
Den som påstår att vi kan förutsäga det framtida klimatet baserat på ofullständiga och ovaliderade klimatmodeller har en hel del kvar att förklara!
Re Ingvar:

Haha, mitt riktiga namn har ingen större signifikans, men jag kan utan problem akademiskt skjuta sönder vilken svensk professor som helst inom matematik, siffror, numeriska metoder, statistik, matematisk statistik osv.
Vad jag i övrigt gör, så gör jag faktiskt ingenting för att förbättra situationen nuförtiden annat än att jag för lite roliga debatter på diverse forum, när tiden räcker till och intresse finns. Däremot pysslade jag en del med undervisning för nått decennium sedan mm. Jag slutade med det när vi fick en ny professor i matematik, som, visade det sig inte hade en enda publikation förutom ett papper med 20 författare där bidraget bestod i att byta ut en fyrkants sida mot en cirkels diameter av exakt samma längd i en algoritm känd sedan 1930-talet. Professorn var alltså politisk professor snarare än en matematisk professor.
Nu sysselsätter jag mig med annat.
Re Thomas #13:
Polynomanpassning är långt ifrån någon väg till sanningen oavsett hur många termer som inkluderas i ekvationen. Ifall du studerar den rörelsefrihet som polynomet får pga. antalet inkluderade termer så kommer du snabbt att inse att det är de geometriska begränsningarna i lineariteten i kombination med feltermerna som till synes avgör hur väl man tycker att polynomen passar data. Märk väl att det finns ett oändligt antal andra funktionsformer, vilka har betydligt större rörelsefrihet än att addera olika konstruktioner av data (X1^2, X2^3, X1^4, log(X5) osv. Ingen sådan funktionsform kan på något vis användas för att matematiskt fastställa kausalitet eller exempelvis fastställa en enskild faktors ”bidrag” till en summa (exempelvis mängden koldioxid i atmosfären eller prognosticera utvecklingen av en summa som en funktion av ökning eller minskning av någon enskild terms data i ekvationen).
‘The only thing necessary for the triumph [of evil] is for good men to do nothing’
ANNONym xxx, du har en intressant framställning. Hoppas att vi får mera draghjälp av dina kunskaper. Ingenting är väl så logiskt som matematiken, men den måste användas på rätt sätt inom sitt begränsningsområde. Det är intressant det du skriver om kausaliteten. Finns det någon matematisk form där man har kausalitet mellan punkterna i en kurva?
Man kan säga ganska mycket om framtida klimat, t ex att det är väldigt troligt att klimatet om 10 år i Sverige är mycket likt det klimat vi har idag – det kommer med största sannolikhet (>99.9% säkerhet?) inte vara bli lika varmt som i dagens Kongo, eller lika kallt som i Arktis.
Sedan kan man ju kanske inte förutsäga medeltemperatur eller medelnederbörd, eller andra klimatparametrar, under t ex åren 2020-2030 med en viss, önskad noggranhet.
Så då är frågan, vad innebär att ”förutsäga klimatet”? Vad menar t ex Leujene när han skriver ”den som påstår att vi kan förutsäga det framtida klimatet baserat på ofullständiga och ovaliderade klimatmodeller har en hel del kvar att förklara!” eller Björn när han säger ”Eftersom klimatframtiden är okänd, måste dessa prognoser som IPCC saluför, vara bedrägligt lurendrejeri.”?
Menar de att vi inte alls kan ana vilken sorts klimat vi kommer ha om 10 år, eftersom framtiden till viss del är okänd? Menar de att IPCC inte kan förutse framtida förändringar av klimatet? Eller menar de att IPCC:s osäkerhetsintervall (som ju, av skäl som vi t ex förstår m h a detta blogginlägg, är väldigt vida) är för snävt, och att den precisionen är omöjlig? Vore intressant med lite längre förklaringar om vad var och en egentligen menar.
Jag köper inte påståenden om att eftersom något delvis är osäkert så vet vi ingenting alls om det, och de som säger saker om detta begår ”lurendrejeri”.
*glömde ett att i sista meningen: …och att de som säger saker om detta begår ”lurendrejeri”.
ehm, vänd på saken och utgå ifrån att klimatet är övervägande stabilt. Det vet vi mycket om. Varför då anpassa livet till osäkra datamodeller?
Framtiden är inte kalkylerbar. När skall vi få beslutsfattare som begriper detta och handlar därefter?

Det skulle kunna bli ganska intressanta beslut
Fast varför besluta något alls om framtiden ändå inte kan förutsägas.
Ingenting du gör kan ju få några förutsägbara konsekvenser.
The Dice man som statsminister
Magnus # 25
Jomenvisst! Det gick ju bra i riksdagen, så varför inte?
Magnus [25]; Det handlade om matematik. Du kanske kan förutsäga klimatutvecklingen med matte? Jag anser att de som påstår att de kan göra det, antingen inte förstår vad de själva uttalar, eller att de helt enkelt gör ett medvetet bedrägligt uttalande.
Som artikelförfattaren, Anonym och andra (implicit) påpekar så är statistik en del av matematiken och säger alltså inget om verkligheten. Den ger oss blott ett bekvämt sätt att presentera data – det är allt. Det intressanta är ju de klimatologiska regimer (naturliga trender) som dessa data förhoppningsvis återspeglar och som statistiken kan bidra med att avslöja för oss. Se vidare:
https://www.klimatupplysningen.se/2011/04/24/sondagstankar-om-trender/
Det problem som man oundvikligen stöter på här är det logiska gapet mellan en ändlig mängd data och de prognoser (och generella naturlagar) som de baseras på. Detta problem går under namnet induktionsproblemet inom filosofin – och är olöst (därför tror jag mer på falsifierbarhet än bekräftelseforskning i vetenskapliga sammanhang). Man kan alltid konstruera ett oändligt antal kurvor som ”fits the data”. Följaktligen är varje prognos som följer en viss kurva lika sannolik som någon annan. (Strängt taget är sannolikheten för varje prognos lika med noll!)
Därför kommer man egentligen ingen vart bara med kurvanpassning. Man måste utgå från klimatologiska teorier som har andra utgångspunkter i mer grundläggande teorier.
Just för globala medeltemperaturen de senaste 150 åren går det också bra med en anpassning som innehåller en rät linje och en trigonometriskt serie. Den rusar inte iväg före eller efter dataseriens intervall och har en lite mindre trend än anpassningen med bara den räta linjen. Att lägga till en periodisk serie är heller inte bara en grundlöst påhitt. Vissa forskare påstår att det finns en (sol)cykel på 60 år i temperaturdata, även för vissa proxydata.
År 1861 började vice amiralen Robert Fitzroy utfärda stormvarningar för fiskare och sjömän. Fitzroy var inte bara grundare till nuvarande Met Office i England, han var också kapten på Beagle under världens kanske mest berömda seglats, dess världsomsegling 1831-36. Känd som Charles Darwin’s världsomsegling. I själva verket var Darwin’s huvuduppgift att hålla Fitzroy sällskap. Fitzroy var en utomordentlig observatör och skaffade sej under sina år till sjöss för sin tid otroliga väderkunskaper. Trots det var förstås hans underlag för stormvarningarna bristfälligt och de mötte våldsam opposition från tidens vetenskap med Royal Society i spetsen. Efter hans förtidiga död 1865 inställdes varningarna, men fiskarna tvingade fram ett återupptagande efter par år. Detta är typiskt för meteorologin (och kanske andra prognosinriktade discipliner): Prognosverksamheten börjar väldigt tidigt, nog alldeles för tidigt. Dock, den fortsätter pga starkt tryck utifrån.
AnonymX bekräftar att den rena matematiken och statistiken inte har mycket att komma med här. Det är inget nytt, tvärtom nästan trivialt. Nu har man dock numeriska modeller som med avsevärd skicklighet förutsäger vädret några dygn framöver. Möjligt, eftersom modellerna hela tiden verifieras, testas, mot verkligheten. Prognoserna är inte perfekta, långt därifrån, men de har blivit mycket bättre, förbättras fortlöpande och lämnar samhället värdefull info.
Fortfarande utfärdas prognoser för längre tid, månader och årstider, på väldigt svaga grunder. Resultaten blir därefter.
Detta prognosmeteorologins öde (eller förbannelse) har klimatologin övertagit då den blivit klimatprognostik. Man släpper glatt ut scenarier för klimatet om hundra år. På sätt och vis riskfritt, eftersom de inte kan verifieras förrän så lång tid förflutit att de glömts. Dock, alltför många politiker och journalister uppfattar dem som säkra prognoser. Denna det europeiska etablissemangets nuvarande övertro på dem kan stå oss dyrt. Vem behöver f.ö. känna till klimatet om hundra år? Något tiotal år framåt är angelägnare. En ljusglimt är att SMHI nu söker utarbeta metodik för prognoser 15 år framåt. Dem får man möjlighet att verifiera och även om uppgiften förefaller omöjlig kan man inte utesluta framgång.
Klimatproblematiken tycker jag att signaturen ehm i # 22 har sammanfattat bra.
Såväl meteorologin som klimatologin fordrar observationer. Som naturligtvis inte heller är perfekta, men oundgängliga och verkligen användbara. Vad skulle vi veta om atmosfären och klimatet utan dem? För såväl modeller som observationer gäller att de inte får övertolkas. Något som alltför ofta sker med ”trender”. Vi må vara hur ense som helst om att trender inte kan extrapoleras framåt, i praktiken görs det. Med mitt inlägg vill jag visa att trender måste tolkas försiktigt. De är förrädiska. Komplicerade trender kan vara rent vilseledande. Trenders längd har jag inte tagit upp. Rent parodiskt är när man i klimatologi talar om trender på något tiotal år.
Kanske beskrivs trender bäst av ekonomen Alec Craincross (1911-1998)
A trend is a trend is a trend,
But the question is, will it bend?
Will it alter its course,
Through some unforeseen force,
And come to a premature end
Tage #30
Jättebra dikt!
Den skulle nästan tåla en upprepning på söndag. Eller vad säger du Lena – är regeln att det skall vara nyskrivet?
/C-G
Ingemar Nordin # 28 : Jag ber att ännu en gång få citera Alf Henrikson : ” När man minns hur tokigt man tänkt och hur fel man fått och hur annorlunda det faktiskt i regel har gått och hur världen har drabbats av sällsamma metamorfoser, får man årligen mindre och mindre respekt för prognoser”. Jag tror mer på observationer, demonstrationer och experiment än på IPCC:s prognoser, som verkar vara tagna ur luften. Mvh, Håkan.
Tyvärr kan vi ju inmte göra oberoende experiment med vår jord för att använda till modelbygge. Det man får göra är att använda en tidsperiod för att ta fram modellen och en annan tidsperiod för att validera modellen så jag håller inte med om ”eftersom det saknas oberoende data att testa dem mot är de icke verifierade och deras prognosförmåga okänd, sannolikt mycket låg” och visst kan man göra vettiga black-box modeller enbart baserat på mätdata után att blanda in fysiken. Om dessa modeller klarar valideringsteset så kan de sannolikt anvädas för vettiga prognoser. I min senaste blogg ger jag ett enkelt exempel som visar att CO2 är en trolig orsak till temperaturstgringen.
Stickan # 33 : Fysikaliskt sett kan CO2 omöjligen orsaka temperaturhojningar om den inte hämtas varm ur skorstenarna. Första vibrationsnivån, som nås när molekylen absorberat ett kvantum IR-strålning med våglängden 4,3 eller 15 my är inte metastabil som vissa nivåer i CO2-lasern och har därför en tillåten övergång till grundtillståndet. Detta sker ögonblickligen eftersom vibrationerna ger molekylen karraktären av en dipolantenn. Den hinner inte avbörda sig den upptagna energin genom stötar med luftens molekyler. Den själv och omgivande molekyler värms ej upp och den del av strålningen som hamnar på jordytan kommer från jordytan, så inte heller den blir varmare. Mätningar och experiment visar att så kallade växthusgaser inte medför någon ”växthuseffekt”. Vill man göra modeller utan att blanda in fysiken kommer man att misslyckas, vilket framträder med full evidens. Mvh, Håkan.
Re Björn #21:
Kausalitet är idag inte möjligt att bevisa matematiskt. Kausaliteten som sådan är en flum-teori uppfunnen med vetenskaplig diskussion som främsta syfte och syftar främst till hypoteskonstruktion utifrån data som är högst ovetenskapliga rent bevismässigt. Enligt kausalitets teorins hårdare tolkning så kan man vara 100% säker på kausalitet vid datafenomen av specialfall av sorten som kallas för multikollinearitet på samma teoris språk. Exempelvis från den traditionella fysiken sträckan=farten x tiden osv.
Vad man kan göra idag med kombinationen av samplingteorin (fundamentet i den matematiska statistiken) och experimentteorin (där man försöker utröna effekten av olika faktorer) genom att kombinera dem och sedan replikera undersöknings-experimentet tills kritikerna är övertygade är att inom ramen för tyckande återupprepa undersökningsexperimentet på ett sådant vis att man på ett övertygande vis kan utesluta alla störfunktioner som exempelvis samplingförfarandet (detta är nödvändigt), mätinstrumenten samt övriga felkällor. Man vill alltså kunna påvisa att enskilda faktorers förändring har betydelse.
För att illustrera svårigheterna i att tillämpa sådan nödvändig teori på klimatet så kan man säga att exempelvis statistik producenter som SCB inte klarar av det. Medicinföretagen och svensk medicinforskning klarar inte av det. Fysikernas samlade forskningsresurser klarar inte av det osv. Vad gäller klimatforskningen så har de hittills inte genomfört en enda acceptabel förenklad experiment. De har alltså ingenting att visa upp utom en massa ”slarvdata” (läs gärna skitdata) som de sedan modelltrixat med på ett sätt som får grundkurs studenter i internetenkäter att framstå som duktiga vetenskapsmän. Det är alltså högre vetenskaplig nivå på vilken tidnings eller affärs internetenkäter än vad det är på klimatforskningen, men forskningspengar fördelas helt uppenbart inte efter vetenskaplig förtjänst och merit, som vi alla vet.
Re Ehm #22:
IPCC:s prognosmetodik avseende hockeyklubban och liknande har vi avverkat rätt rejält i den här tråden. Men det finns mer avseende just prognoserna och 2 ax av intressant information är just matematiken i det hela.
För det första säger matematiken att den inte kan användas på det vis som IPCC vill göra överhuvudtaget. Så vad IPCC gör i sina ”antaganden” är att de dels hittar på att data är ett ”stort” slumpmässigt urval från hela världen och att alla delar av världen hade exakt lika stor sannolikhet att komma med i samplet och detta i kombination med påhittet att klimatdata skulle vara ”normalfördelat” över hela jordgloben.
När det sedan gäller prognoserna så bygger de på två delar:
Det påhittade samplet från den påhittade normalfördelningen OCH den angivna modellen (som de själva yxat till en hockeyklubba). Prognosen kommer sedan av variationen från samplet i kombination med modellen samt den felterm som enbart ”can be estimated..” från sampeldata och modellen. Feltermen har sedan en osäkerhet som sträcker sig från +oändligheten till -oändligheten. Så modellen i sig eller prognosen utesluter alltså inte oändlig kyla eller oändlig hetta ifall man pratar temperaturer, detta dock med låg låg sannolikhet. Så prognosens sannolikhetsmassa kommer alltid att vara störst i den riktning som modellen pekar…. eller med andra ord så är modellen och processen helt subjektiv eller bad science rakt igenom.
Re Ingemar #28:
Utan att vara klåfingrig så ska jag påpeka några saker i ditt inlägg #28.
Induktionsproblemet och alla saker som har med ”oändliga data” att göra är alltid frånkopplade från varandra.
Vad gäller prognoser baserat på korrekt implementerad teori så säger matematiken att det går att prognosticera exempelvis en summa eller medelvärde vid en tidpunkt t baserat på ett sampel taget vid tidpunkt t och placera detta i ett intervall. Sannolikheten för att lyckas krympa detta intervall till en punkt på en imaginär eller skala utanför heltalen är däremot exakt noll rent matematiskt.
Vad gäller kurvanpassningen så har du helt rätt, man måste använda andra metoder i klimatfallet, för med kurvanpassning kan man aldrig nå vetenskaplig konsensus (riktig konsensus alltså).
John von Neumann formulerade väl den klassiska kommentaren om värdet av ”curve-fitting”:
”With four parameters I can fit an elephant and with five I can make him wiggle his trunk”
Re Tage #30:
Jag skulle nog vilja påpeka att matematiken och statistiken och den matematiska statistiken ligger omkring 100 år före alla numeriska läror, datalogi osv. vad gäller modellhantering av alla slag. Ditt inlägg låter lite som snorunge som lånat pappas bil och utnämner sig till bättre bilist än pappa utan körkort.
Alla sådana där numeriska läror har en ”pappa” som hör hemma i matematiken, statistiken eller den matematiska statistiken. Ingen numerisk lära har någonsin lyckats avancera beyond ”pappa” och ”pappa” var oftast en inkompetent pajas, som inte var tillräckligt ”fin” för att få leka med de andra matematikerna och därför beslutade sig för att ägna sig åt datalogi eller numeriska metoder istället.
Inget papper inom numeriska metoder eller datalogin har hittills tillfört matematik, statistik, eller matematisk statistik något utan är teorimässigt kvar i 1910-talet. Detta gäller även väderprognoserna.
Stickan #33,
Det man får göra är att använda en tidsperiod för att ta fram modellen och en annan tidsperiod för att validera modellen
Tyvärr är det lätt att tro på denna illusion. Men eftersom man inte klart skiljer på utvecklingsfasen av modellerna och valideringen av dem så handlar det om en selektering av modeller snarare än om en validering av dem. Varför skulle man lita på modeller som selekterats ut därför att de klarar av att rekonstruera två tidsperioder istället för en? Det finns fortfarande i princip ett oändligt antal tänkbara modeller, med helt olika prognoser för framtiden, som klarar av det.
ANNONym #39 För att fortsätta liknelser (möjligen roliga, garanterat haltande) är jag snarare pojken som sitter vid pappas avancerade PC och (förgäves) försöker lära honom använda den.
Jag betvivlar inte att matematiken och statistiken nått längre än meteorologin och klimatologin men beklagar att de inte använder kunskaperna för att revolutionera dessa tydligen efterblivna discipliner.
Stickan #33, Ingemar #40
Det man får göra är att använda en tidsperiod för att ta fram modellen och en annan tidsperiod för att validera modellen
En skillnad mellan väder och klimatmodellerna är att för väderprognoser finns oberoende observationer i form av historiska fall. Och det kommer snart nya. I tid omfattar de nämligen några få dagar. Klimatmodellerna omfattar sekler och så långa observationsserier finns inte. Radiosonderingar t.ex. finns bara sedan ett drygt halvsekel.
Vädermodeller kan man alltså testa mot andra tidsperioder än de som använts vid utarbetande av dem. Det räcker inte att testa mot endast ett fall. För klimatmodeller finns inte en enda annan tidsperiod.
Re Tage #41:
Jag har inte för avsikt att spendera någon större tid på att debattera med dig. Dock vill jag påpeka att numerologin, datalogin etc. hittills inte har kommit med några nya resultat. I övrigt så har alla tunga ”resultat” inom databeräkningsområdet gjorts av just matematiker, statistiker och matematiska statistiker.
Som slutpoäng vill jag nog hävda att hela databranschen har sitt ursprung i just matematik, statistik och matematisk statistik. Att sedan många inom matematik, statistik och matematisk statistik inte vill befatta sig med datorer handlar om saker som språkvård, opålitlighet map. definitioner och beskrivningar samt förstås ett bristande intresse för just teknik. Andra av samma sort, oftast sämre gillar att grotta ned sig i komplexa simuleringar, främst för att dölja bristerna i sina resonemang och språkförmåga.
ANNonym din argumentation påminner om ett gammalt talesätt: ”Enligt aerodynamiken kan humlan inte flyga”. Du hävdar att: ”enligt matematiken och statistiken är numeriska väderprognoser, NWP, omöjliga”. Vi vet alla att humlan flyger och NWP fungerar.
Betr temat för mitt inlägg, trender, är vi ju ense, fast mina argument inte duger för dej.
Re Tage #44:
Alla möjliga resultat som man kan komma fram till med hjälp av numeriska metoder, beräkningslära, simuleringar osv. är redan kända inom matematik, statistik och matematisk statistik. Poängen som du har missat är att dessa databeräkningsläror bara är en pytteliten del av matematik, statistik och matematisk statistik.
Din argumentation är på väldigt låg nivå, läs student på grundkurs men en korrekt tolkning av diskussionen är att någon sifferbaserad prognos av vädret aldrig kan bli bättre än vad matematiken bakom prognosen förutsäger, detta gäller i högsta grad databeräkningslärorna. I övrigt så verkar SMHI samt övriga prognosmakare var lika klagade på idag som för femtio år sedan men vad gäller väderkunskaparna så verkar de inte ha någon större insikt i någon teori bakom prognoser.
Vad gäller trender så är en trend bara en definition av tillstånd, vanligtvis så kallas trend för den generella riktning som något tillstånd förflyttar sig emot medan ”matematiska” trender oftast definieras genom någon form av uppdelning av en tidsserie i olika komponenter. Begreppet trend är alltså ganska meningslöst utan ett avgränsande definition.