To provide the best experiences, we use technologies like cookies to store and/or access device information. Consenting to these technologies will allow us to process data such as browsing behavior or unique IDs on this site. Not consenting or withdrawing consent, may adversely affect certain features and functions.
The technical storage or access is strictly necessary for the legitimate purpose of enabling the use of a specific service explicitly requested by the subscriber or user, or for the sole purpose of carrying out the transmission of a communication over an electronic communications network.
Den tekniska lagringen eller åtkomsten är nödvändig för det legitima syftet att lagra inställningar som inte efterfrågas av abonnenten eller användaren.
The technical storage or access that is used exclusively for statistical purposes.
Den tekniska lagringen eller åtkomsten som används uteslutande för anonyma statistiska ändamål. Utan en stämningsansökan, frivillig efterlevnad från din Internetleverantörs sida, eller ytterligare register från en tredje part, kan information som lagras eller hämtas endast för detta ändamål vanligtvis inte användas för att identifiera dig.
The technical storage or access is required to create user profiles to send advertising, or to track the user on a website or across several websites for similar marketing purposes.

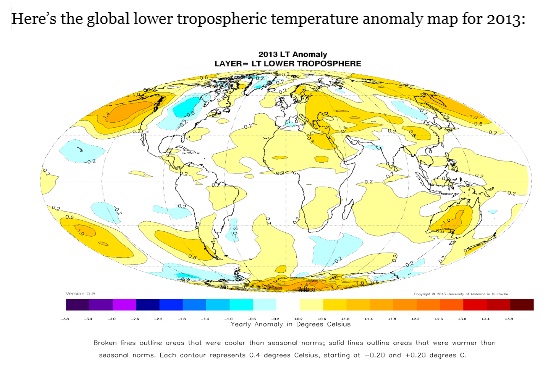
Det ser ju inte speciellt oroande ut. Men om man vill spinna på detta så skulle man kunna rubriksätta artikeln:
”Den fjärde högsta globala temperaturen någonsin uppmätt!
😉
Bäckström
Tror du har satt rubriken för SVT och SR redan.
😀
Om man vill se något positivt på kartan så ser man ju att Grönland har varit ovanligt kallt under 2013.
#1. Vaddå? Trots all koldioxid (livets gas, växternas och därmed vår mat) vi producerar blev år 2013 knappt ens det fjärde varmaste året på 30 år. Ynkliga 0,27 grader skulle ingen märka något av om inte meteorologer med dyra och känsliga instrument och superdatorer att leka med talade om det för oss. Kom med något bättre om du vill skrämmas.
Ytterligare ett år kallare än 1998 har gått!!
Warmth from 1998 were are thou ?
Tro inte att solcykel 24 är över ännu. Det ser ut att bli ett andra maximum innan solfläcksaktiviteten går ned under 2015.
http://www.thegwpf.org/sunspots-2013-winter-solstice-surprise/
http://www.solen.info/solar/
Om solen har ett inflytande över den globala temperaturen så lär det dröja innan vi kan se någon effekt av detta.
Litet förtydligande
December +0,27
2013 total +0,24
Rätt ska väl vara rätt.
Ingemar
We cannot rule out that variations in solar radiation has affected the global temperature in the past or whether it will do so in the future. However the main point is that presently we have neither any empirical evidence supported by reliable observations nor any credible dynamical theory of the sun that indicate that such variations can occur.
Before we can be serious about this we must built it on something credible.
Lennart
Bilder är lite som text. Så fort något blir satt på pränt blir det sant. Nu vet jag inte om just den bilden i inlägget är sann eller inte. Det jag vill påpeka är ett mänskligt fenomen, som förmodligen bottnar i den mänskliga psykologin, hur hjärnan skapar den verklighet vi alla dagligen upplever och skapar oss själva i den verkligheten, precis som att den är sann.
Att se en bild är nästan magiskt övertygande, för det är det som vår hjärna gör allra bäst, analyserar bilder och propagerar resultatet genom flera filter tills det beskärda resultatet till slut når medvetandet i sin mest relevanta form för överlevnad.
Man skulle, som en del gör, kunna hävda att människan är den tänkande apan som betvingar världen. Det kan knappast vara mer fel. Människan är den kännande apan som agerar på samma sätt som för tusentals år sedan. Om det prasslar i löven så spring. Det är en stabil evolutionär algoritm. Att stanna kvar och analysera om det är en tiger eller en råtta… ja, det säger sig själv.
Hela den här AGW-debatten kommer snart att ebba ut, liksom alla tidigare debatter i samma härad. Människan som art är sinnessjuk i någon bemärkelse. Den måste hela tiden hitta ett yttre hot att sysselsätta sig med. Den som känner sig manad kan ju räkna upp alla dessa.
Tillägg:
Gail Tverberg, som är betydlig mer påläst och kunnig än jag, säger i sitt senaste läsvärda blogginlägg:
”The primary way of dealing with limits seems to be “solutions” dictated by concern over climate change.These solutions are of questionable benefit when it comes to the real limits of a finite world, but they do make it look like politicians are doing something useful. They also provide a continuing revenue stream to academic institutions and “green” businesses.”
http://ourfiniteworld.com/2014/01/02/why-a-finite-world-is-a-problem/#more-38698
Är det någon som läst Michael Crichtons State of Fear? En underhållande bok, Själva storyn är naturligtvis ren sci-fi eller kanske snarare technothriller. Dock är människorna och deras reaktioner och motiv kusligt lika verkligheten. Fullständig oförmåga att ta till sig andra åsikter som om de är robotar som programmerats. De blir arga på huvudpersonen som kommer med fel budskap.
#10, Fredrik Berg
Har inte läst den boken, men noterar att i alla sci-fi-böcker jag läst har författaren tagit en redan existerande verklighet som utgångspunkt och sen skruvat den några varv. Och vissa författare kommer förstås att rent statistiskt få helt rätt, medan de flesta får helt fel. Det kanske är det som skiljer bra från dåliga författare.
I efterskott kan jag se att Artur C Clarke hade ganska rätt i vissa saker. Dock återstår ganska mycket att besannas.
Chrichton har källhänvisningar bak….det är rätt ovanligt med ”ren” sci-fi 🙂
Kalle #8
Det ligger mycket i vad du skriver. Men ändå har du helt fel.
”Man skulle, som en del gör, kunna hävda att människan är den tänkande apan som betvingar världen. Det kan knappast vara mer fel. Människan är den kännande apan som agerar på samma sätt som för tusentals år sedan.”
Du kan väl inte förneka den enorma skillnaden mellan människan och andra djur när det gäller att förutsäga och hantera händelser i vår omgivning.
Jämför med en häst, som tar prasslet prasslet från ett kolapapper i diket för ett möjligt lejon och faller i sken. Ingen som helst moderering i beteendet.
Och att bara se människan som en icke tänkande utan bara kännande apa är bara defaitistiskt.
Vem springer för att det prasslar i buskarna? Vi kollar väl bara i smartphonen, gäspar, och går vidare.
Fredrik #10
Ja, jag har läst den. Och det är inte en av Chricktons bästa böcker.
En bok som man typiskt väljer från bestsellerhyllan på flygplatsen, för att fördriva några timmar vid gaten eller på planet.
Men den är lite pojkboksaktig tycker jag. Enkel intrig, förutsägbar, och med övertydliga karaktärer.
Han har skrivit bättre böcker.
Oj, nu skrev jag Chrickton fas han heter naturligtvis Crichton och inget annat.
Sitter med hans Disclosure framför mig för att få stavningen rätt.
Den tycker jag var bättre, men har naturligtvis en helt annan bakgrund.
Nu fann jag den i bokhyllan.
800 sidor i paper-back upplaga (inkl appendici och referenser)!
Kanske borde läsa om den. Ingen skriver väl så mycket utan goda skäl.
Och det måste medges att han var rätt tidigt ute med sin avklädning av alarmismindustrin.
Eftersom detta är en UAH-tråd måste jag givetvis visa mina grafer och fråga var man ser någon uppbromsning:
År för år, de senaste 30 åren, nu komplett med december.
http://www.bilddump.se/bilder/20140104095005-83.233.174.89.JPG
Medelvärde per 5-årsperiod, de senaste 30 åren
http://www.bilddump.se/bilder/20140105073552-83.233.174.89.JPG
Var är uppbromsningen?
UAH, senaste 26 åren i rullande 5-årsmedel med total trendlinje (0,017 grader per år i ökningstakt) och trendlinjer för varje 5-årsblock (utom sista som är 6 år).
http://www.bilddump.se/bilder/20140105092035-83.233.174.89.JPG
Sträck upp handen den som ser nån ”hiatus”, ingen ökning de senaste 17, 15 eller 10 åren, kraftig uppbromsning etc.
Uppbromsningen framgår fortfarande bäst ur mätdatat. Årsvis filtrerat tappar man en del relevant information, men i första bilden i #17 syns fortfarande vad det är frågan om.
#20
Handen upp…
De senaste 10 åren har en trend på sådär 0,004°/år, dvs oskiljbar från noll (har inte räknat exakt med senaste värdet).
Hela 30-årsperioden har en trend i stil med den som du anger i första figuren, dvs ca 4 ggr större.
Att reducera ner datamängden med 60 ggr från originaldatat är en för grov nedsampling för att kunna yttra sig om enstaka 10-årsperioder, som då bara får två datapunkter.
JonasN och Christer E.
Om man har hypotesen att temperaturanomalierna är resultatet av en trend med en överlagring av slumpmässiga variationer som kan både öka och minska trenden,är då inte ett rullande 5-årsmedel relevant för att dämpa fluktuationerna som jag visar i #18?
Alternativt att titta över en längre period som jag gör i #17.
JonasN efterlyser mätdata, nåväl, tittar vi på en längre serie från Woods på UAH får vi samma, nästan, årliga trend som i alla mina grafer, 0,016,jag får 0,017
http://www.woodfortrees.org/plot/uah/from:1983/to:2014/plot/uah/from:1983/to:2014/trend
Man ser alltså trenden direkt även på månadsdata om man tar lite längre perioder (då de slumpmässiga variationerna hinner cancellera ut varandra och slumpavvikelsen får mindre relativ betydelse alternativt använda glidande medelvärde som jag gör i #18.
På korta tidsserier får de slumpmässiga variationerna för stort genomslag då dels cancelleringen inte hinner ske i samma utsträckning och dels ordningen av toppar och dalar får för stort genomslag för att trenden ska vara relevant.
Christer E.Du bör nog titta noga på grafen i #18.Där är de sista 10 åren inte reducerade till 2 punkter.
BjörnT,
Du kan givetvis ha hypotesen att det finns långsiktiga trender som störs av kortsiktigare variation. Den hypotesen har vi nog allihopa i olika grad. Själv tror jag att vi nu har en uppåtgående trend i 1500-årscykeln (senaste minimum var LIA) och samtidigt en nedåtgående trend i större skala (senaste maximum Holocena optimum).
Men du kan inte utesluta en avstannad trend med en så grov nedsampling du gör. I #18 gör du en annorlunda bearbetning av grunddatat och anger ingen trend för de senaste 10 åren (dock tydligt påverkad av blippen 2008/2010) men nog är trenden även där betydligt lägre än för alla 30 åren.
Givetvis får din nedsampling lägre betydelse över längre perioder som i #21. Det var därför jag accepterade din 12 ggr nedsampling i mitt första svar som approximativt trenden för hela datat och hela perioden.
Om vi lyfter blicken behövs givetvis mer tid för att avgöra om nuvarande uppehåll fortsätter, säger sig själv. Men att säga att uppvärmningen fortsätter som vanligt när det inte varit någon alls på 10 år och pendlar på gränsen till signifikans över 15 år eller så låter ju liksom inte rimligt. Det är ju också som jag och Jonas brukar påpeka, enligt klimatmodellerna skulle uppvärmningen inte bara fortsatt, utan accelererat. Och så stannar den istället. För varje år som fortsätter så här blir kraven på snabb uppvärmning allt större framöver för att ”hinna ikapp”. Och då larmas det för fullt just nu om det senaste alstret i Nature som anger 3,2° uppvärmning till år 2100, dvs 0,04° grader per år eller tio gånger snabbare än hittills detta årtusende…
Christopher E. I #18 visar jag trenderna för varje period av fem fem-årsmedelvärden även om det bara är grafiskt och jag inte tar med trenden numeriskt. Du kan se med blotta ögat att de fem senaste punkterna som representera de sista 10 åren haren betydligt brantare lutning än 0,004.
Men vi får se hur det blir!
#24
… och likväl är trenden i originaldatat fortfarande 0,004 utan olika typer av processande och nedsamplande av datat, som alla ger olika resultat.
Det har inte blivit varmare på 10 år, hur mycket lutande trender man än ritar över det i snitt platta datat.
Jag antar att månadsvärden är startprodukten för UAH-datasetet, för med tanke på satellitbanorna och hur ofta varje ytenhet avläses känns inte högre upplösning som tex dygn rimlig.
Ska vi enas om att vi får se?
Christopher # 20
Vad ”slarvigt” av dig att endast ange temperaturtrenden i tusendelar av en grad, när uppenbart många hypokondriker lider av temperaturändringar mycket mindre än så. Tänk en hel hundradels grad temperaturförändring på tio år!
Vad jag inte begriper, är att någon överlever temperaturskillnader på hela tio grader, eller mer, från natt till dag.
Att dela upp temperaturen i hundradelar, eller tusendelar, av en Celsius-grad, tillför inte klimatdebatten annat än rena löjligheter.
I klimatdebatten finns det gott om förstå-sig-påare som hävdar att en temperaturökning på 0,7 grader under den senaste hundraårsperioden är karastrofal.
Kan någon med säkerhet känna av en temperaturförändring så liten. Svar nej.
I klimatdebatten ser vi ständigt att till och med någon enstaka hundradelsgrad, eller till och med tusendelsgrad, av temperaturförändring utgör katastrofala faror inför framtiden. Är dessa människor medvetna om att temperaturskillnader i den storleksordningen s a s finns på varenda meter ute i den fria luften. Alla som har tillgång till en digital utomhustermometer kan dessutom se att temperaturen hela tiden, inom bara några sekunder, förändras med många gånger flera tiondelar av en Celsiusgrad.
Lena Krantz och alla andra artikelförfattare på klimatupplysningen, varför bemöter ni aldrig skrivelser, där det hänvisas till hundradelsgrader, eller tusendelsgrader, på exempelvis mitt enkla sätt att beskriva sanningen??
Olav Gjelten: Du begår ett kategorimisstag av monumentala mått. Det är därför ingen orkar kommentera dina argument.
Olav,
Det som bland annat jag och BjörnT talar om här, är egentligen mer matematiskt. Alltså vilken trend datat visar. Det är inget löjligt med det. Huruvida siffrorna är märkbara eller av någon praktisk betydelse är en helt annan fråga. Givetvis är också decimaler långt till höger inom felmarginalerna för att mäta en ”global temperatur”, så dessa små trender kan vara en chimär.
Inte tror jag egentligen inte heller 0,7° i snitt, över mer än hundra år dessutom, har någon betydelse av mått. Detta även med hänsyn till att det är en genomsnittssiffra där enskilda platser värmts upp mer och andra avkylts. Jag tror inte någon plats på jorden har väderförändringar utöver vanlig variation i kortare tidsskala som utan statistiska övningar går att upptäcka under en livstid.
Men det är som sagt en annan diskussion än ”uppvärmningsplatån”.
#21
Om man har hypotesen att där finns en underliggande (sann) trend i brusiga och/eller fluktuerande mätdata kan man räkna ut sannolikheten för att denna trend skall ligga inom ett visst intervall, baserat på den antagna(!) förutsättningen att där dels finns en linjär trend, och att variationerna kring denna är Gauss-fördelade (eller ja, man kan låta ett enkelt statistikprogram göra detta).
Gör man det får man fram hur sannolikt denna (antagna!) trend ligger inom vissa gränser, ifall hypotesen stämmer och avvikelserna är just Gauss-fördelade.
Stämmer inte båda dessa antaganden, får man inte ens det. Då betyder svaret ännu mindre. Vad man då får är bara värdet på sannolikheten för fallet ifall man hade haft precis samma data, men att detta hade styrts av en linjär trend plus överlagrat brus med samma fördelning.
Om man inte förstår ovanstående, eller skillnaden mellan de två bekrivna fallen bör man nog avstå från att prata om ’underliggande trend’ eller vad den skulle ha för värde och vilken betydelse det värdet då skulle ha …
Att 30-årstrenden är ngt helt annat än den för de 10 senaste åren är precis vad diskussionen handlar om. Speciellt om man dessutom betänker att den 30-årstreden ju inkluderar även de sista 10 årens mätdata.
Ni som fäster stor uppmärksamhet på tusendelsgrader, som kan uppgå till en hundradelsgrader om tio år och möjligen tiondelsgrader om hundra år. Längre än så kommer ni aldrig, då historiens alla fakta talar för att trenden bryts långt innan vi kan tala om globala temperaturförändringar av hela grader och som skulle ta tusen år att åstadkomma. Detta gäller temperaturer uppåt. Eftersom vi med stor sannolikhet befinner oss på tröskelen till en ny istid, kan vi emellertid på sikt förvänta oss temperaturfall på åtskilliga grader.
Christopher # 29
När vi talar om globala temperaturer skall vi heller inte glömma att många små och avlägsna väderstationer lagts ner. Dessa stationer var i huvudsak belägna på kalla platser. Hur många sådana t ex lades inte ned i det enorma Sovjet, när det kolapsade?
Att gamla lantliga observationsplatser efterhand kom att ligga i urbana områden är ett annat fakta som fått den globala temperaturen att klättra.
Undrar hur mycket av de skarva 0,7 graderna som har sin bakgrund inom bara dessa två nämnda exempel. Det kanske till och med räcker för att komma fram till att vi överhuvudtagit inte har haft någon temperaturstegring de senaste hundra åren?
Jonas #30. För att göra det du säger behöver man nog åtskilligt mer mätdata än det vi har. Ren slump kan spela roll med så få mätdata och troligen är det ingen gaussiansk fördelning på slumpfaktorerna heller, troligen mer nån slags power-fördelning på dom.
Hursomhelst ser man en tydlig trend på 30 års data och den består på kortare tidsserier när man gör glidande 5-årsmedelvärde som tydligt framgår i #18
Olav,
Jag håller med dig om en del. Det stämmer att man inte kan extrapolera trender under långa tidsrymder (det finns en kommentator här som älskar att göra det). Det stämmer troligen också att en del av de 0,7° är värmeö-effekt och inte allmän uppvärmning. Fast bara en mindre del, för det finns ju data rätt opåverkat av lokala effekter som visar uppvärmning senaste 30 åren.
Däremot spelar det ingen roll om kalla stationer läggs ned, för medelvärdet är anomalier och inte ett medelvärde av absolutvärden. Det som spelar roll är om andelen stationer med lokala ökande effekter tex från urbanisering ökar.
Björn T #18
Visst har du fått fram en snygg kurva. Vad jag undrar över är hur den skulle ha sett ut utan de två stora vulkanutbrotten El Chichóns på 80-talet och Pinatubos på 90-talet. Under tvåtusentalet har vi varit förskonade från sådana stora vulkanutbrott med en sådan klimatpåverkan. Var för sig fick dessa vulkaner medeltemperaturen att gå ned ca 0,5 grader.
I engelska wikipedia sägs det om El Chichón ”The total volume of the eruption was much smaller than the famous eruption of Pinatubo in 1991; however El Chichón’s impacts were equally as significant on global climate.
The eruption injected 7 million metric tonnes of sulphur dioxide(SO2) and 20 million metric tonnes total of particulate material into the stratosphere, which circulated the Earth in three weeks. The eruption occurred just as the largest El Niño of the century was initiating, because of this several scientists suggested that the El Chichón eruption caused the El Niño. However, climate modelling and detailed studies of past eruptions and El Niño have shown that there is no plausible theories connecting these two events, and that the timing was merely a coincidence.”
El Chichón inte bara sänkte medeltemperaturen utan den maskerade även den dittills största El Niño som var på gång sägs det.
Det skulle vara intressant om du kunde göra en kurva som var korrigerad för dessa båda stora vulkanutbrott och den nästan uteblivna El Niñon. Givetvis blir det en del gissningar men eftersom vi inte har motsvarande utbrott efter år 2000 borde det tas med på något sätt tycker jag.
Då skulle vi få en riktigare kurva över temperaturuppgången.
Christopher E
”Däremot spelar det ingen roll om kalla stationer läggs ned, för medelvärdet är anomalier och inte ett medelvärde av absolutvärden. Det som spelar roll är om andelen stationer med lokala ökande effekter tex från urbanisering ökar.”
Kunde du förklara det här så att lekmän också förstår?
#36 Guy
Jag inte världens expert själv… men det skulle inte fungera att bara ta det värde som står på termometern (absolutvärdet) för alla stationer, lägga ihop dem och göra ett medelvärde. De behöver korrigeras i så fall, i första hand för höjden, för det blir ju kallare högre upp. Att det är så kallt på Grönlandsisen tex beror ju på att det är uppåt 3000 meter över havet. Men nere vid byn i fjorden är det kanske plusgrader samtidigt.
Istället är det betydligt smidigare att ha en etablerad referensnivå för varje stations temperatur baserad på medelvärdet under en basperiod. Och sedan istället rapportera avvikelsen (=anomalin) från det medlet (=normalen).
Så en station i Ryssland kanske rapporterar en anomali på -1,4℃. En i Sudan +0,5℃ och en i Motala +1,1℃. Att det själva verket är -43℃ i Ryssland, +38℃ i Sudan och +5℃ i Motala spelar ingen roll.
Därför spelar det ingen roll för den globala anomalin om en plats har kallt, hett eller tempererat väder normalt. Och den globala anomalin stiger inte för att en station just i Ryssland läggs ner.
Problemet med nedlagda stationer är ett annat. De som läggs ner i första hand är de som ligger långt ut i obygden och är dyrast att sköta. Kvar blir flygplatser, trädgården utanför Meteorologiska Institutionen och liknande. Inte heller det skulle spela roll om de var stabila från påverkan, det är ju anomalin som används. Men det är just vad urbana stationer inte är. Flygplatser och städer växer, ytor hårdbeläggs, våtmarker omkring dikas ut. Effekten är välkänd och dokumenterad, korrelationen mellan grad av uppvärmning och städers storlek tydlig. Så när andelen urbana stationer ökar införs i ökande en falsk anomali som beror på urbanisering. visst, det ÄR ju varmare där man mäter, men de får också representera en stor yta landsbygd som inte värmts upp på samma vis.
Denna station i Queensland, Australien ingår i det globala medlet. Om svarta bilar blir trendiga där lyser anomalikartan mörkröd för ett ansenligt område!
http://www.john-daly.com/ges/surftmp/images/tewantin.jpg
Som en fotnot är det globala medlet av den verkliga temperaturen (vid havsnivå) normalt någonstans nära 15 grader.
#33 Kort svar: Nej! Längre svar: Nästsista stycket i #30
Tack, Christopher E. Bra förklarat. Man kan ju, om man är lite elak, säga att den globala tempen höjs på grund av lättja och sparåtgärder. Konstigt med tanke poå hur lätt det är i dag att fjärravläsa stationer. Ytterligare med tanke på hur dyra datamaskiner meteorologen håller sig med.
Christopher
Jag tackar dig för dina vänliga svar. Nu är jag så ändå obildad att jag inte förstår att det inte spelar någon roll för resultatet att hela rader med kalla observationsplatser lagts ner senan början på 1990-talet.
Jag har för övrigt läst debattartiklar där man ställt frågan att det varma 1990-talet kan ha haft sin grund i den ensidiga nedläggningen av just köldhålsplatser.
#40 Olav
En historia som just berör Ryssland är att det sägs att städer fick tilldelning av statliga medel beroende på kallt där var. Så det ledde till att för låga temperaturvärden rapporterades… När Sovjet föll försvann den politiken och det var ingen mening att ljuga längre. Så i början av 90-talet syns en hastig uppvärmning över främst Sibirien.
Till hur del detta är en skröna kan jag inte avgöra.
#40 Olav
Jag är ingen expert på området men ett exempel kan kanske förtydliga skillnaden. Säg att du vill kolla på medeltemperaturen i Sverige och du har bara tre mätstationer, en vid Umeå, en vid Gävle och en i Skåne. Var och en får representera en tredjedel av landets yta. Normalvärdet för basperioden exempelvis 1961-90 är då säg +3, +5 och +7 respektive. Om var och en får representera en lika stor yta blir då medel +5 för Sverige.
Säg nu att ett visst år råkar temperaturerna vara +3,5 resp +5,4 resp +7,3. Temperaturavvikelsen är då +0,5 resp +0,4 resp +0,3 dvs i medel (om alla mätpunkter reprsenterar lika yta) +0,4 dvs +5,4 i medeltemp för sverige.
Säg nu att du detta år i själva verket inte fick några mätvärden från Umeå (den kallaste stationen), då stationen blev nerlagd, hur skulle du då göra för att beräkna medeltemperaturen i Sverige detta år.
Ett sätt vore ju att ta medelvärde för återstående stationer (Skåne och Gävle) och låta var och en representera halva Sverige. Det ger 12,7 delat med 2= + 6,35. Om man gör på detta (korkade) sätt kan man förledas att tro att medeltemperaturen detta år var 6,35-5=1,35 grader varmare än normalt när det i själva verket ska vara 0,4 grader varmare än normalt. Jag antar att det är denna effekt du tror att man får om man lägger ner en kall station.
Ett alternativt sätt är att ta medelvärdet av temperaturavvikelserna av återstående mätstationer och låta dessa respresentera hela landets temperaturavvikelse, dvs 0,4 + 0,3 delat med 2 = 0,35. Eftersom vi vet att normaltemperaturen för landet normalt är +5 får vi då +5,35 som årets temperatur dvs enbart 0,35 varmare än normalt. Alltså MINDRE än de 0,4 grader varmare som vi fått om vi haft tillgång till värden från Umeå. Med andra ord kan en nedläggning av en station med kalla temperaturer (men större positiv anomali) förleda oss till att tro att avvikelsen är mindre än vad den är.
Ytterliggare ett sätt att förfina vore ju att låta Gävlemätstationen (som ligger närmare Umeå) få representera en större del av landets yta säg 2/3 då vi har ett bortfall av en mätstation. Då hamnar vi på +0,367 i medelanomali och en uppskattad medeltemp för landet det aktuella året på 5,367 vilket är ytterliggare närmare det ”verkliga” värdet (med alla mätstationer). En del skulle kanske säga att man då manipulerat mätdata när man ger en station större vikt men det blir ju mer korrekt kanske…
Det fina med anomalier är att de (tror jag) varierar mindre med yta än temperatur (är det en ovanligt varm sommar i Stockholm är det ofta det i Västerås också). Det kan till viss del se på kartor på smhi.se
Nu har jag ingen aning om vilka stationer som lagts ner som du menar i #32 men om det är så att de är i Sibirien som ligger närmare polartrakterna (och därför är kalla men som förväntas få en större tempökning (anomali) än medel för jorden) så kan det alltså bli den omvända effekten mot för vad du tror dvs att man skulle få en underskattning av temperaturökningen. Dock tror jag du kan vara lugn för att de som ägnar åratal på heltid åt detta är medvetna om svårigheterna och att de knappast begår sådana enkla fel som att inte justera (på bästa möjliga sätt) för svårigheterna med att mäta jordens medeltemperatur på ett sätt som är jämförbart över tid.
Christopher E och Jonas N och alla andra .
Studera denna graf:
http://www.bilddump.se/bilder/20140107105907-95.199.0.57.JPG
Här har jag på en underliggande trend på 0,014 slumpat ett värde mellan -0,03 och 0,03 i 30 punkter.
Som synes får jag 30-årstrenden hyfsad nära, den ligger på 0,016 men kolla trenden på de sista 10 punkterna, den ligger på 0,0046! Dessa sista 10 punkterna är alltså en delmängd av de första 30 punkterna.
År det något som känns bekant?
Jag har just demonstrerat hur en ren slumpfaktor kan få det att se ut som en stadig trend som syns på 30 årsdata nästan helt försvinner om man separat analyserar de sista 10 åren.
QED.
Samma förutsättningar som i #43.
http://www.bilddump.se/bilder/20140107113428-95.199.0.57.JPG
Här har jag också visat att det summerade 5-årsmedeldatat över de sista 10 åren kan ha samma lutning som datat över 30 år, trots att 10-årsdatat ger en helt annan och betydligt flackare trend.
Detta inträffar inte alltid men det kan inträffa. Därmed har jag byggt en modell som efterliknar läget för UAH datat det senaste 30 åren och gett en möjlig förklaring till den skenbara uppbromsningen; att den är helt och hållet en artefakt av slumpmässiga förändringar men den underliggande trenden är oförändrad.
BörnT
Vad du demonstrerat är att du ännu inte förstått vad diskussionen handlar om. Som påpekats många ggr kryllar det av folk som börjar i helt fel ände och hävdar att där finns ’underliggande trend’ och tom att den är oförändrad, varefter de ägnar resten av tiden åt att resonera om varför den inte syns just nu …
Som sagt, de ’vet’ svaret, och letar efter ’metoder’ och ’data’ som bekräftar det de redan vet eller vill ha sant. Dvs raka motsatsen till ett vetenskapligt förhållningssätt.
Men det är ju inte direkt ngt nytt. Eller hur?
😉
Jojo JonasN. Jag förstår att allt du har att komma med är att stå och muttra något om ovetenskaplighet.
Men med detta http://www.bilddump.se/bilder/20140107105907-95.199.0.57.JPG har jag demonstrerat att detta http://www.woodfortrees.org/plot/uah/from:1984/to:2014/plot/uah/from:1984/to:2014/trend/plot/uah/from:2004/to:2014/trend
har en logisk förklaring
Dvs att ett urval av en kortare tidsserie i en längre skenbart kan få en betydligt flackare trend än den längre pga rena slumpfaktorer.
I detta fall finns en robust teori om mekanismen av temperaturökningen: utsläpp av växthusgaser, det finns en robust observation, att temperaturen under den senaste 30-årsperioden (enligt UAH) har växt med ca 0,017 grader per år (Woodsgrafen 30 år, kolla raw data undergrafen) och så finns det en bevisad mekanism som förklara den skenbara uppbromsningen de sista 10 åren med en tillväxt på bara 0,004: en ren slumpvandring, se min graf ovan som övertydligt emulerar detta. Se #43 för beskrivning vadjag gjort.
En prydlig och sammanhängande kedja som bygger på robust teori, robusta observationer och en demonstrerad mekanism. Brukar vara kriterier på vetenskaplighet.
Och allt du kan göra är att muttra och gestikulera Jonas N. Fast ingen skulle väl ha förväntat sig att du skulle säga som det är: Jo BjörnT, logiken är oklanderlig, det skulle kunna vara som du säger men min fasta tro övertygelse och kommer du ändå inte att rubba.
BjörnT, du behskrev själv att du först bestämde dig för ’facit’ och sedan slumpade brus ovanpå det. Antingen på riktigt, och då fick du hålla på många ggr för att få ngt du ville visa upp, eller så sa du bara att du slumpade punkter, men ’slumpade’ dem så att de visade vad du ville.
Som sagt … Inget nytt där.
Jag tycker att du skall hålla dig till att räkna ut medelvärden, skriva dem på lappar, dra ifrån eller lägga till dem (och spara lapparna). Jag tror nämligen att du klarar sådant. OK, du får leka med excel också, men prata helst inte om trender och vad de betyder …
Som många ggr förr har det skorrat illa under dina diarré-dumpningar. Men jag har avstått från att kommentera oftast.
Och ja, Al Gore trodde ocksås detta du beskriver var vetenskap, ’settled science’ tom … jojo, inget nytt där heller!
JonasN Nej jag tog fram en hypotes och bevisade att den stämde. Sorry I came in like a wrecking ball in your världsbild….. 🙂 du hittar nog någon annan vetenskap att misstänkliggöra! Passiv rökning eller asbest vekar ligga dig varmt om hjärtat!
48 BjörnT 2014/01/07 kl. 22:01
”Nej jag tog fram en hypotes ”
Bespara Klimatupplysningen med dina privata bilder o forskning!
Du fäktar tom värre än en intermittent vindfjolla. Har inte Du heller någon stoppknapp?
Jasså Björne?
Du har tagit fram en hypotes, och bevisat ett den stämde?
🙂
Du har pratat om ett rakt streck och genom diverse filtreringar (eller borttagande av information) sagt att man fortfarande kan dra detta raka streck och att det fortfarande är rakt då, och nästan lika snett som det långa ursprungliga.
Så nej, du har inte kommit med något av substans alls, du verkar inte ha förstått mycket heller om vad det handlar om, och verkar fortarande inte förstått hur off du är och har varit här …
Sorry, but no cigar!
PS Minns du när du la till banal information (1*1=1 eller ngt liknande) i ett underbestämt ekvationssystem, och trodde att du ’kreativt’ kommit på hur det plötsligt inte längre är icke-inverterbart? Eller förstod du inte ens efteråt att du avslöjade djup okunskap samtidigt som du trodde du gjort ngt fantastiskt? Om du har förtängt det skall jag låta bli att påminna dig. Men vad du gjort nu är inte mycket bättre DS
Som sagt Jonas N och Pär Green. Gestikulera och muttra är allt som återstår. Ni har exakt samma sätt att resonera på och tycks ha ungefär samma kunskapsnivå.
Grattis till att ha funnit varandra! 🙂
PS Jonas N Jag vet att du blev avis när jag tog fram även matris nr 2 och visade hur den kunde användas för att transformera en uppsättning mätdata till anomalidata OCH TVÄRTOM i en enda respektive matrismultiplikation men jag trodde du kommit över det där. Men det finns terapeuter, eller är det detta vetenskapsförnekande enligt ovan som är din terapi?! 🙂
BjörnT,
Det är ingen lösning eller bevis att säga ”vi har egentligen samma uppvärmning de senaste 10 åren som under en längre tidigare period, men slumpfaktorer har maskerat den.”
Det är enligt mätdata ingen uppvärmning under denna period hur man än försöker trixa till det.
En gängse ”etablerad vetenskap” skulle dessutom inte ens uppvärmingen ha fortsatt, den skulle accelererat. Det är alltså inte samma förutsättningar under 30 -årsperioden heller, det senaste årtiondet har växthusgasutsläppen som enligt ”konsensus” är drivande för uppvärmingen varit betydligt större än tidigare.
Det senaste alarmistalstret i Nature (Sherwood) anser att uppvärmingen nu med omedelbar verkan ska accelerera 10 ggr (!) för att hinna ikapp skräckprognosen. Tro det….?
Christopher E:
Ingen uppvärmning? Rullande femårsmedel enligt UAH:
http://www.bilddump.se/bilder/20140105092035-83.233.174.89.JPG
Från avdelningen ’Det är värre än vi nånsinn trodde’:
Slå upp ’Rullande medelvärden’!
BjörnT #51
Som sagt, du har inte förstått mycket av allt du gestikulerat om. Och jo, du la till din sparade fusklapp (vilketförstås är enklaste metoden) genom att skriva upp en idiotisk matris (innehållandes fuslkappen förstås) + en extra rad/ekvation i vilken du räknade ut att 1*1=1.
Och du tror att det är ngt andra skulle vara avis på!
Grattis till en självkännedom i nivå med sådana Gunbo tror sig kunna avgöra utan att förstå ämnet!
😉
JonasN: Som sagt, fäkta med armarna är du bra på. Bildligt talat.
Du blandar ihop detta med ’att veta vad jag pratar om’ …
Och det finns en anledning till att den metoden är närmast okänd för dig.
😉
JonasN: #54. Vad är det du inte förstår med ”rullande medelvärde”? Ska jag förklara för dig?
#53
Nej, där är ingen uppvärmning de senaste 10 åren. Det hjälps inte vad du gör. (Jag betraktar både trenden på 0,004 och nettoändringen som oskiljbara från noll i detta fall).
Eftersom du nu valt rullande medelvärden som går 4 år bakåt i tiden från varje punkt har du dessutom med flera år med data från före den period vi diskuterar…
Jonas #55. Jojo…jag insåg att du kunde göra om den affina transformationen till en linjär, genom att öka antalet rader och sedan visade jag hur man med en enda matrisoperation kunde gå från mätdata till anomalidata och tillbaka. Allt medan du fäktade med armarna och pysslade med förklenanden ad honimem babbel för att försöka dölja att du var bortgjord.
Cristopher E #59. Jag föreslår att du tittar på grafen
http://www.bilddump.se/bilder/20140105092035-83.233.174.89.JPG
en gång till.
De fem punkterna längst till höger representerar de senaste 10 åren!
Trenden på dessa fem punkter är långt ifrån dina ”nära noll”,
#61 BjörnT
Så nu vill du använda bara fem datapunkter för de senaste fem åren, vilka förresten inte får med alla 10 åren i sin medelvärdesberäkning (det missade du). Ett väldigt osymmetrisk förfarande, med 2004 alltså uteslutet, och 2005-2008 endast representerade i medelvärden från och med värdet 2009. Du kan inte använda löpande medelvärde för 5 år för att dra slutsatser om 10 år.
Du gör det bara mer och mer komplicerat för dig själv.
När är trenden bara 0,004 i alla fall, vilket alltså är inte bara nära noll, utan riktigt nära noll. December 2003 var förresten anomalin +0,367°, tio år senare december 2013 var den +0,27°… för att tala om annat än ”trender” också.
http://www.woodfortrees.org/plot/uah/from:2004/to:2014/plot/uah/from:2004/to:2014/trend
Varför komplicera det?
(Woodfortrees tycks inte ha decembervärdet 2013 med ännu, men det är försumbart för denna diskussion).
Christopher E #62
”När är trenden bara 0,004 i alla fall, vilket alltså är inte bara nära noll, utan riktigt nära noll.”
Stopp och belägg! På bara 10 000 år betyder det en ökning på 4 grader!
Dessutom blir det ännu högre temperatur på våra nordliga grader kanske 6-8 grader varmare, lokalt ännu värre!
Det är också hög tid att vi lägger ner alla kärnkraftsverk och ersätter dem med hållbara energislag som tex väderkvarnar och installerar propellrar på bilarna som då kan driva bilarnas batterier helt gratis. Vi bör också sluta med att använda datorer och alla andra grejer som går på el, då slipper vi ju att producera så mycket energi.
😉
#63 Bäckström
”Stopp och belägg! På bara 10 000 år betyder det en ökning på 4 grader!
Dessutom blir det ännu högre temperatur på våra nordliga grader kanske 6-8 grader varmare, lokalt ännu värre!”
Skulle det vara sant är det bara en fördel, för annars kan nedanstående bild illustrera vart den riktiga ”underliggande” trenden egentligen tar oss i den tidsskalan. Valfri plats ovanpå inladsisen över Sverige:
https://earthdata.nasa.gov/sites/default/files/styles/large/public/2009_antarctica_landscape.jpg
😉
ChristerE #62.
Tack för påpekandet, nu blev det ännu tydligare vilken trend de sista 10-åren ger med rullande 5-årsmedel
🙂
http://www.bilddump.se/bilder/20140108153410-83.233.174.89.JPG
Bäckström #63
Så LBt har alltså en avbytare?
Otaliga gånger har det förklarats varför ett sådant resonemang inte är hållbart. De som är klimatsmarta inser att en global temperaturförändring på 0,0004K inte är mätbar. Det verkliga värdet kan lika gärna vara 0 eller -0,0004. Att då sitta och räkna ut var man kommer att hamna om 10000 år är meningslöst.
#65 BjörnT
Problem med bilddumpsservern? Får inget på länkarna nu, men provar senare.
Men hur datat än masseras är trenden fortfarande 0,004 i sin ofiltrerade form, så vi kan hålla på med detta hur länge som helst. Jag vinner ändå. 😉
Du kan inte i en diskussion som rör de senaste 10 åren bara använda en delmängd data, osymmetriska medelvärden eller löpande medelvärden som av nödvändighet inbegriper data före dessa 10 år.
Ett annat sätt att se är det är att din övertygelse om en underliggande trend även senaste årtiondet bygger på ett förmodande om framtiden, att uppvärmningen fortsätter. För i sig själv är det givetvis helt absurt att tala om en trend på 0,017 när den bevisligen är 0,004 enligt datat.*
* (en brasklapp till Olav mfl. Jag är helt införstådd med att diskussionen är teoretisk. Varken UAH eller andra tillgängliga serier har upplösning nog att visa så små trender som är aktuella här.)
Björn, jag vet inte hur länge du följt klimatdebatten. Du har använt löpande medelvärden bakåt i tiden. Men jag minns när det från officiellt håll dök upp en klimatkurva med symmetriskt löpande medelvärde (det är ju det normala) som inte bara gick enda till då innevarande år utan också böjde upp misstänkt i slutet. Hur var det möjligt? Jo, det hade använts modellerade prognosvärden från framtiden i medelvärdet när de riktiga mätvärdena tog slut. Ridå… 🙂
#66 Perfekt
Du missade inte ironin hos Bäckström, väl…?
BjörnT, du hade behövt veta vad ’rullande’ syftar på i rullande medelvärden innan du skrev det. Ledsen, men jag har tappat räkningen på alla dina (oprovocerade) maglask.
Vad du möjligtvis visade var linjära trenden genom styckevisa femårsperioder.
Att du bara ids att göra dig till clown med sån’t eftertryck!
😉
Och nej, du verkar fortfarande inte har en susning om vad ’transformationer’ är till för. Allt babbel du kommit med har varit så nedlusat med strunt att man nästan, men bara nästan, tycker synd om dig. Hur är det det? Fick du inte tillräckligt med beröm när du gjort ngt bra när du var liten? Eller varför håller du på som du gör nu?
Jonas N: Du vet uppenbart inte vad varken rullande medelvärde eller en linjär transformation är.
51 BjörnT 2014/01/08 kl. 07:16
”Som sagt Jonas N och Pär Green. Gestikulera och muttra är allt som återstår. Ni har exakt samma sätt att resonera på och tycks ha ungefär samma kunskapsnivå.”
Ditt favorit uttryck är Ad hominem-argument om andra!
Hur skall då ditt påstående uppfattas?
Men du, en energiproduktion utan startknapp o stoppknapp fungerar inte!
Sluta att fäkta med dina bilder o vindfjollor.
Ad hominem-argument eller argumentum ad hominem (latin ”argument mot personen”), är ett osakligt argument och därmed ett argumentationsfel eller felslut inom retoriken som handlar om en argumentatörs karaktär, förmåga eller avsikter i stället för själva sakfrågan. Ett ad hominem-argument kan antingen vara ett personangrepp eller ett genetiskt argument.
Personangrepp har ofta syftet att nå psykologiskt övertag över motståndaren och få denne på defensiven i debatten. Elaka personangrepp är något som undviks av den retoriskt kunnige, eftersom de lätt kan få den motsatta effekten: den angripne får medkänsla och sympati från åhörarna och därmed en fördel.
Genetisk argumentation innebär att man låter trovärdigheten hos en tes avgöras av vem/vilka som argumenterar för eller mot tesen. Detta är irrelevant, och således är genetisk argumentation en typ av ignoratio elenchi. Genetiska argument kan vara både positiva och negativa.
Argumentum ad hominem kan också användas i betydelsen att man appellera till en person eller grupps ”fördomar, intressen eller fattningsförmåga utan att stå i något logiskt sammanhang med det diskuterade.”[1] Eller ett argument som i sin slutsats vilar på meningsmotstånadrens premisser, och användas för att överbevisa denne, då premisserna inte bestrids av densamme.[1]
http://sv.wikipedia.org/wiki/Ad_hominem-argument
BjörnT, ’Transformationer’ och vad de gör eller används för är långt ovanför ditt huvud, men enkla medelvärden säger du ju dig klara av (även om det emellanåt blir väldigt skakigt).
Googla på rullande medelvärden eller som det normalt kallas ’glidande medelvärden’
Fast Jonas, här uppfattade jag det som om Björn verkligen använde rullande/löpande/glidande medelvärde över 5 år, till skillnad från tidigare då han använde ett medelvärde vart 5:e år. Han använde dock en osymmetrisk variant, enbart bakåt, vilket jag inte tycker är det bästa då datat som ingår i en punkt blir onödigt avlägset. Jag undrar om det inte är Excel själv som har den preferensen, dock.
BjörnT, nu funkar bilddump igen. Jag ser att du ökat till 6 år för att få med 2004. Men fortfarande gäller vad jag skrev i #67.
Christopher E #68
Tyvärr har det blivit ”normalt” att folk uttrycker sådana vanföreställningar, därför missade jag faktiskt ironin. Jag hade inte blivit förvånad om LBt tubbat någon mindre vetande person att understödja hans ”resonemang”
Christopher
I #18 visar Björne en bild som han påstår innehåller ’rullande’ femårsmedelvärden, men med styckevist anpassade 5-års trender.
Och det han kallar rullande femårsmedelvärden’ tycks innefatta data ända fram till 2013.
Möjligtvis är punkterna han redovisar ’släpande femårsmedelvärden’ men det är inte vad han hävdade.
Poängen är dock samma som den varit hela tiden (precis som tidigare tillfällen) att dessa ’efterhandsjusteringar’ av data inte ändrar ett dyft i de faktiska förhållanden. En annan poäng vore att att han ständigt försöker med saker som ligger lite(?) bortom hans fattningshorisont. Speciellt då han ju faktiskt redovisat rätt tolkning av rätt data dessutom.
JonasN #376. Du har fel som så ofta. Du har blandat ihop rullande medelvärden med rullande centrerade medelvärden. Men det är lite gulligt med dina magistrala uttalanden som ständigt slår fel. 🙂
Definition av rullande eller glidande medelvärde som det också kallas.
http://www.manufacturingterms.com/Swedish/Simple-Moving-Average.html
”glidande medelvärde, även kallad rullande genomsnitt, rullande medelvärde”
”Ett glidande medelvärde används ofta med tidsseriedata för att jämna ut kortsiktiga fluktuationer och belysa långsiktiga trender eller cykler. ”
JonasN det är nog dags att gå till klassrummet: http://www.scb.se/Grupp/Klassrummet/_Dokument/Skolan301.pdf 🙂
Christopher E#74. Jag ser att du lite försiktigt vågat dig på att påpeka för JonasN att han har fel 🙂 Grattis du är nog den enda som har samma grundåsikt som honom som vågat dig på att påpeka en av hans många tabbar.
Men låt oss diskutera sakfrågan efter JonasNs felaktiga inlägg om rullande medelvärden.
Läs igenom denna mening noga.
”A moving average is commonly used with time series data to smooth out short-term fluctuations and highlight longer-term trends or cycles.” http://en.wikipedia.org/wiki/Moving_average
Det är därför jag anser att ett rullande fem-årsmedelvärde är ett relevant sätt att ta fram den långsiktiga trenden.
Det vill säga om man har hypotesen att det finns en underliggande trend som höjer den globala medeltemperaturen beroende på ökningen av växthusgaser i atmosfären och det dessutom finns slumpmässiga variationer som både ökar och minskar medeltemperaturen, är då inte ett rullande medelvärde är en bra metod för att försöka eliminera slumpmässigheten och ta fram den underliggande trenden?
Om svaret är nej får du gärna motivera svaret. Och innan du formulerar ditt svar läs igenom Wikipedia-citatet noggrant. Och kolla länken igen.
http://www.bilddump.se/bilder/20140108153410-83.233.174.89.JPG
Christopher E. Jag tror att du har kapacitet att hänga med i detta resonemang.
Antag att det finns en affärskedja som säljer vinterkläder. För tio år sedan sålde man för i snitt 1500 (1000tal) kronor. Försäljningen är dock starkt säsongsberoende med peak i december förstås och låga siffror i maj-augusti. Tillväxten har i genomsnitt varit ca 10 procent varje år, varje månad för sig, men i praktiken har tillväxten varierat sätt på ett slumpmässigt mellan 0 och 20 procent under varje enskild månad, jämfört med året innan, så det är inte exakt
Om man nu har en tillväxt på exakt 10 procent i genomsnitt månad för månad och säljer 1500 i snitt basåret så får man en ökning månad för månad på nästan 20 (enkelt att räkna ut). Dvs efter 10 år 120 månader säljer vi för i snitt för ca 3900.
Men nu var det som sagt inte exakt 10 procent, utan det fanns en viss slumpmässighet, dock centrerad runt 10 procent. Vi kan ta fram trenden för försäljningsökningen de 10 åren genom att plotta försäljningssiffrorna varje månad och genom regressionsanalys ta fram trenden.
Detta är gjort i den vänstra grafen här:
http://www.bilddump.se/bilder/20140109082421-83.233.174.89.JPG
I den mittersta grafen visas istället ett rullande 12-månadsmedelvärde med trend. Skillnaden mellan dessa två grafers trender är inte så stor som synes. Vi ligger på en trend på ca 18 (1000tal) ökning varje månad alltså lite mindre än 10 procent i årlig ökningstakt.
Nu vill Christopher E köpa denna butikskedja. Han begär givetvis in försäljningssiffrorna så han kan göra sig en uppfattning om framtida värde, speciellt vill han veta om vilken tillväxttakt han kan förvänta sig baserad på historiska siffror.
Genom en serie olyckliga omständigheter så har all försäljningsstatistik utom för de sista 2 åren utplånats.
Christopher E får alltså bara de sista 24 månadernas försäljningsstatistik.
Han ber sina två, som han uppfattar det, mest matematikkunniga bekanta om hjälp få fram trenden. Det är Jonas N och det är BjörnT.
Jonas N plottar de 24 månadernas data och får fram trenden 42,9 .Björn T plottar istället de rullande 12-månadsmedelvärdet och får fram trenden 18,6.
På vilken av dessa herrars analys bör Christopher E basera sig på för att bestämma vad han kan tänka sig att betala?
Alternativt vilken av dessa två metoder är bättre för att få fram den långsiktiga trenden?
Den högra grafens 24 månadsvärden är den vänstra grafens sista 24 månader, av 120, värden.
Om du har redovisat släpande 5-årsmedelväden är det OK, vad menar du att dina dessutom anpassade styckevisa 5-årstrender skulle visa, när de anpassats till redan (släpande) 5års-medelvärden?
Noterar att du som så ofta (och så vanligt bland klimathotstroende) hittar på helt egna berättelser som de menar skall visa nåt. Rent trams.
Angående dina ’rullande medelvärden’ finns det väl utvecklade metoder att hantera data och dra slutsatser ur dessa. Även att flitrerar dem. Du verkar obekant med de flesta analysmetoder och snickar ihop egna (nu tex dubbel-filtrerade) men förstår forfarande inte vd diskussionen handlar om.
Inget svammel kommer ändra på detta
#79,80 BjörnT
Jag hade inte köpt någon affärskedja baserat på två års så hoppiga data oavsett hur det filtreras! 🙂 Inte på statistik alls vare sig från dig eller Jonas. Efterfrågan är lurigt att förutsäga, några milda vintrar kan slå sönder de bästa affärsdrömmar i vinterklädsbranschen. Långsiktigt hade jag lutat på mig produktkvalitet och marknadsföring och inte på utvecklingen hittills, som inte säger något om framtiden i detta fall. (En annan populär metod numera är ju att köra en undermålig produkt, men lobba framgångsrikt för subventioner… 😉 )
Annars illustrerar du i #80 vad jag hade tänkt att skriva ändå, att löpande medelvärden har störst nytta i att visuellt dämpa främst en mer eller mindre regelbunden variation, som just årstidsvariation. Ett bra exempel kan vara Keelingkurvan för koldioxid:
http://kids.actewagl.com.au/education/_lib/images/Sustainability/AtmosphericCarbonDioxide.jpg
Även en mer oregelbundet hoppig kurva än bara årstider kan visuellt bli tydligare med löpande medelvärde. Just när det gäller UAH så använder ju Spencer ett centrerat 13-månadersvärde:
http://www.drroyspencer.com/wp-content/uploads/UAH_LT_1979_thru_December_2013_v5.6.png
Men varför tycker jag då inte det är lämpligt att göra trendanalysen på filtrerade data? Det har jag (och andra) egentligen redan förklarat, men ungefär så här:
1. Du säger att det ”slumpmässiga variationer” du vill filtrera bort. Men det är de ju egentligen inte. Vi talar om hur det (nåja, nästan) globala medelvärdet av MSU-mätningar varierar. Vi är intresserade av det något märkliga begreppet ”globalt klimat”. Men alla de varitioner vi ser där beror på summan av olika processer i atmosfär och hydrosfär, de är inte slumpartade. Jag kommer aldrig acceptera resonemang i stil med ”men det skulle blivit varmare om inte det och det maskerat uppvärmningen”. Spelar ingen roll om det är AGW-trogna som vill ta bort El Niños eller skeptiker som vill ta bort vulkanutbrott för att hyfsa statistiken i önskad riktning. Vad vi har är summan av allt och det är den som gäller och faktiskt påverkar oss som bor här på jorden.
2. Jag är med dig om att i långa perspektiv kan man tala om en övergripande trend, och är där ett avbrott någonstans som sedan drunkar i en allmän uppgång så visst är det så. Men det gäller inte om ”avbrottet” är slutet på serien, för vi har ingen aning om hur framtiden ser ut. Om man talar om en ”övergripande trend” som egentligen värmt jorden under de senaste 10 åren fast det inte blivit varmare har man bestämt sig för hur framtiden ser ut. Men vi har avstannad uppvärmning nu. Om det fortsätter så får vi se.
3. Jag tycker rent generellt det är missvisande att räkna statistik på redan filtrerat data i låg upplösning istället för det hela datasetet för perioden. Sedan är det givet att under korta perioder blir det stora fel i vilket fall som helst. Det senaste årtiondet är ett bra exempel med saknad uppvärmning men med en fördelning av ett par stora svängningar som ger vilt skilda resultat beroende på analysmetod.
4. Om man nu ska ska använda löpande medelvärden alls i detta fall så är centrerat att föredra. Om man rent konkret ser på UAH de senaste 10 åren är det svårt att se rimligheten och relevansen i att den sista datapunkten 2013 får med toppen 2010 men missar sänkan 2007 (de enda två större händelserna som avbryter vad som annars är nära en platå under perioden). Med 5-årigt bakåtlöpande medel alltså. I ditt diagram (tex i #65) ser det ut som en kraftig uppvärming från 2012 till 2013 av denna anledning, som du sedan glatt räknar trend på. Fast där inte var någon.
Björne
Du säger att du kör med släpande (du kallar det rullande) medelvärden i #18, men sen anpassar du dessutom korta trender till det redan filtrerade datat (som alltså redovisas i snitt 2½ år för sent). Vad vill du visa säga med detta?
Vad menar du det går att få ut för information på det viset som man inte får ut ur samma (ofiltrerade) data om man analyserar det korrekt (dvs utan flera och godtyckliga) filtreringar?
Du har redan berättat att du vill bevisa en ’hypotes’ som du önskar vore sann, men behöver vaska fram den ’underligande trenden’ (som du alltså vill se) genom att ’tvätta datat’, och nu alltså även senarelägga det. OK. Vi alla vet att det är det du skulle vilja se. Men det du gör är raka motsatsen till hypotesprövning.
Måhända är ditt exempel med att förutse framtida affärer precis samma problem som du tycks ha med temperaturerna. Massor av personer skulle vilja veta i förväg hur priser och kurser på diverse instrument och varor utvecklas framtiden. Och de brukar precis som du mfl dra kreativa streck som skall belägga att framtiden blir ngt visst. Och i regel brukar de lyckas sämre än slumpen med att förutsäga framtiden.
Att analysera befintliga data och jämföra dem med tex antagandet att där skulle finnas en existerande trend är gammal skåpmat. Som du dock inte tycks förstå eller ens vara medveten om.
Varför du så bångsstyrigt försöker med matematiska dumheter har jag ingen aning om. Speciellt när du misslyckats sås kapitalt många ggr redan tidigare. Men kanske försöker du intala dig att du är en naturbegåvning som inte behöver hålla dig till strikta definitioner, metoder eller värderingar, utan bara bluddra på …
Det må vara ditt val, Men jag kan lova dig att du kommer misslyckas varje gång du försöker fubba dig förbi verkligheten på detta eller liknande sätt!
Christopher har också försökt hjälpa dig månag fler än en gång, senast i föregående kommentar. The bottom line is:
There is no way you can determine in advance what part of your (only) dataset should be considered signal and which is noise.
Du tycks vlja kringgå detta faktum precis på samma sätt som du tidigare försökte smyga med fusklappar för att hitta tillbaka, till slut tom inpetat i en matris som dessutom hade en extra meningslös rad (identitet) tillagd. Ledsen gosse, högre verkshöjd än så är det inte på din .. ehrm … intuitivt kreativa begåvning .. eller vad du nu kallade den.
Och möjligen
Christer E #82.
Du inser i alla fall att det blir stora fel under korta tidsperioder och att ett rullande medelvärde kan vara bra för att ta fram trender och filtrerar bort brus.
Varför ett centrerat rullande medelvärde skulle vara bättre än ett vanligt förklarar du inte och det finns nog ingen förklaring heller.
Ditt resonemang i din punkt 4 är ganska belysande. ”Sänkan” är inte 2007 utan 2008. ”Sänkan” är ändå i paritet med topparna på 90-talet, extremåret 1998 undantaget.
Men anledningen till att sista 5-årsmedlet ”drar iväg” är inte bara att nu trillade 2008 över kanten utan beror också på att 2013 var den fjärde varmaste året i UAH. Den sista 5-årsperioden har nr 2 ,4 och 6 på ”varmaste-skalan” och fri från ”sänkan” drar den iväg.
Men bara att du och jag tittar på nitty gritty visar ju att det är absurt att försöka lista ut trenden vare sig den är 0,017, 0,012 eller 0,004 eller helt flack förde senaste 10 åren.
Man ska naturligtvis titta på 30-årsperioden!
http://www.bilddump.se/bilder/20140104095005-83.233.174.89.JPG
eller ännu tydligare i den rullande fem-årsmedlet 30år bakåt som i #65.
Se även graf i #80 som visar hur fel man kan komma med korta dataserier där man inte försökt dämpa bruset.
OK Björne, du säger att du inte förstår varför både smeta ut information (medelvärdesbilda) och att sedan flytta den i sidled (släpande diton, i efterhand) skulle vara sämre. Du tom säger att det nog kan kvitta.
Och så är det nog.
Men det beror forftfarande på att du inte förstår hur man hanterar, analyserar (eller för den delen: Transformerar) data.
Du hade dock inte behövt visa detta under mer än ett år tycker jag. Men fortsätt gärna om du tycker tvärtom
Jonas N: Försök lära dig vad ett rullande medelvärde är i stället för att komma med en massa ovidkommande svammel.
Björn T # 80
”Genom en serie olyckliga omständigheter så har all försäljningsstatistik utom för de sista 2 åren utplånats.”
Var det Phil Jones på UEA som var arkivansvarig?
Bengt Abelsson #87.
🙂
Björne, har du lyckats svara ännu på vad du ville ha sagt i #18? Det är ett tag sen nu? Alltså med att först medelvärdesbilda, sedan flytta informationen i sidled, och sedan göra styckevisa trender genom det datat?
Ovidkommande svammel är ju din melodi.
Jonas N #89. Jag förstår att du inte greppat vad rullande medelvärden är. Och jag förstår att du kommer med ditt sedvanliga lallande för att dölja det. Christopher E har förstått vad det är och förmår diskutera det hela på ett vettigt sätt.
Jag hoppas att du inser att du gör dig till åtlöje?
https://www.klimatupplysningen.se/2014/01/04/2013-enligt-uah/
Är det här det ni debatterar? Kallas rullande medelvärde smooting? William M Briggs har en åsikt om saken på sin blogg: Do not smooth times series, you hockey puck!
http://wmbriggs.com/blog/?p=195
Now I’m going to tell you the great truth of time series analysis. Ready? Unless the data is measured with error, you never, ever, for no reason, under no threat, SMOOTH the series! And if for some bizarre reason you do smooth it, you absolutely on pain of death do NOT use the smoothed series as input for other analyses! If the data is measured with error, you might attempt to model it (which means smooth it) in an attempt to estimate the measurement error, but even in these rare cases you have to have an outside (the learned word is “exogenous”) estimate of that error, that is, one not based on your current data.
If, in a moment of insanity, you do smooth time series data and you do use it as input to other analyses, you dramatically increase the probability of fooling yourself! This is because smoothing induces spurious signals—signals that look real to other analytical methods. No matter what you will be too certain of your final results! Mann et al. first dramatically smoothed their series, then analyzed them separately. Regardless of whether their thesis is true—whether there really is a dramatic increase in temperature lately—it is guaranteed that they are now too certain of their conclusion.
Käre Björne
Du har precis aldrig ’förstått’ att jag inte skulle begripa ngt. Men du har försökt med sådant många ggr.
Som sagt, din nivå är ungefär ’medelvärden’ (och fusklappar)
Du visade i grafen i #18 dels släpande 5-årsmedelvärden, som u benämnde rullande, dock ospecificerat. Och gjorde sedan styckevisa 5-års trender av detta. Dvs först utsmetat (5-års) och sedan sideldes förskjutet (i snitt 2½ år), och därefter dessutom styckevisa 5-årsanpassningar (räta linjer)
Vad menade du att detta skulle visa (alltså till skillnad från hur man normalt analyserar data som varierar/fluktuerar och där man vill undersöka om där finns en ’signal’ dessutom). Så noggrant och korrekt som möjligt. Please!?
(Avstå från att gissa trams om andra, använd inte ord du inte behärskar, slarva inte med benämningar osv. Och ffa: Beskriv det du menar skulle vara slutsatserna och värdera dem? Gärna, om du förmår, hur dessa skiljer sig från reslutatet om man hade gjort på sedvanligt sätt, dvs som hela tiden diskuterats här långt innan du började med dumpningsdiarrén. Please!
Jaa du JonasN. Efter att först inte ens vetat om vad ett rullande medelvärde är (visades i #69) så är du, som vanligt, den egenutnämnde experten som pösmagat förkunnar för andra om saker du egentligen vet absolut inget om.
Men du kanske kan lära dig?!
Börja med att förstå vad jag gör här. Rrrrrrrrrrullande medelvärden.
http://www.bilddump.se/bilder/20140108153410-83.233.174.89.JPG
Som ett litet barn, tönt! (*)
Jag undrade vad du ville visa med dina korta trender av förskjutna femårsmedelvärden. Vet du inte det? Du ar ju fått frågan ett antal ggr.
(*) Medelvärden, det är ungefär så långt du fixar saker. Men inte ens de verkar du kunna ange korrekt. Om du vill se något riktigt korkat angående ngt så enkelt som just medelvärden, tom rullande vs släpande kan du läsa i #84.
Ja JonasN: Och du fixar ju inte ens rullande medelvärden……. 🙂 Förstår att du försöker dölja det genom att veva och fäkta…. 🙂 🙂 🙂
Eller fixa en transformation, i stället blev det ett patetiskt ekvationssystem…. 🙂
Staaaackars JonasN, han vill så mkt men så tokigt det blir…. 🙂
#84 BjörnT
”Du inser i alla fall (…) att ett rullande medelvärde kan vara bra för att ta fram trender”
Nej, det skrev jag inte alls. Faktiskt tvärtom.
”Varför ett centrerat rullande medelvärde skulle vara bättre än ett vanligt förklarar du inte och det finns nog ingen förklaring heller.”
Jo, det gjorde jag. Flera gånger nu. När blev just ett släpande rullande medelvärde ”vanligt”? Är det inte helt enkelt så att Excel inte ger något annat val och du inte listat ut hur du ska kringgå det? Dina tidigare femårsmedel låg ju också på fel plats och du skyllde på Excel när jag påpekade det. Titta på Spencers 13-månadersrullning, han vet hur man gör.
Ditt resonemang i din punkt 4 är ganska belysande. ”Sänkan” är inte 2007 utan 2008. ”Sänkan” är ändå i paritet med topparna på 90-talet, extremåret 1998 undantaget.
”Men anledningen till att sista 5-årsmedlet ”drar iväg” är inte bara att nu trillade 2008 över kanten utan beror också på att 2013 var den fjärde varmaste året i UAH. Den sista 5-årsperioden har nr 2 ,4 och 6 på ”varmaste-skalan” och fri från ”sänkan” drar den iväg.”
Nej, den anledningen är marginell. Topparna är mycket nära, vilket syns tydligt i datat. Att flera varmaste ligger på platån senaste årtiondet säger inget om att uppvärmning pågår. Jag kan ha noll löneökning de senaste 10 åren och samtidigt haft de högsta lönerna i mitt yrkesliv samma år.
”absurt att försöka lista ut trenden vare sig den är 0,017, 0,012 eller 0,004 eller helt flack förde senaste 10 åren. Man ska naturligtvis titta på 30-årsperioden!”
Att det blivit varmare under 30 år är helt okontroversiellt. Problemet uppstår när du försöker hävda att det senaste årtiondet som inte haft någon uppvärmning i själva verket haft samma uppvärmning som fortsätter som tidigare.
Vad gäller absurt, kan jag med min bakgrund tycka att det är absurt med hysterin kring marginella trender på både 30 och 100 års tid. Under 8000 år är trenden tydligt avkylande. Med ditt sätt att resonera har vi haft avkylning de senaste 100 åren. Jag kan säkert producera en trend med lämpligt nedsamplade medelvärden som visar detta.
Blev ett fel i #96…
Missade citationstecken och kommentar till ett stycke. Kommer här:
”Ditt resonemang i din punkt 4 är ganska belysande. ”Sänkan” är inte 2007 utan 2008. ”Sänkan” är ändå i paritet med topparna på 90-talet, extremåret 1998 undantaget.”
Stämmer, jag skrev fel år i hastigheten där (men i tex #23 skrev jag 2008). Har dock ingen betydelse eftersom året i båda fallen hamnar utanför sista 5-årsmedlet. Att sänkan liknar någon topp i tidigare årtionden är helt ovidkommande, jag diskuterar platån senaste årtiondet, och inget annat.
#90
”Christopher E har förstått vad det är”
Jag är absolut ingen virtuos på statistik, det ska erkännas, men jag läste ändå lite matematisk statistik på matematiska institutionen på Lunds universitet en gång i tiden, så vi hoppas att lite fastnade i alla fall, även om inriktningen då var biologisk provtagning och inte meteorologisk. Rullande/glidande medelvärden var inget nytt i just denna diskussion. 😉
BjörnT, läs förresten i #91…
”you absolutely on pain of death do NOT use the smoothed series as input for other analyses!”
😉
Christopher E #98
Citat:
”..läste ändå lite matematisk statistik på matematiska institutionen på Lunds universitet en gång i tiden..”
Jag hoppas att du då mötte Georg Lindgren, som jag har stor förtroende för. De använder matematisk statistik för att beräkna risken för ”hundraårsvågor”och andra extremer som sedan används vid t.ex. dimensionering av oljeplattformar i Nordsjön.
Risken för antropogena klimatförändringar behandlar de på fikarasterna.
En av hans adepter flyttade till Chalmers under 2013 och jag kan bara undra hur det fungerar vid fikabordet där. 😉
Länk:
http://scholar.google.se/citations?user=G7BfJUMAAAAJ&hl=sv
Ok, så du vet alls inte vad du ville visa med dina streck i #18. Tänkte väl det. Istället kommer du med idiotiskt aptjatter. Du har ju försökt med sådant förut, dvs snacka total dynga i månader för att dölja hur väck du var/är.
Transformationer är långt över ditt lilla huvuvd, gosse. Behöver jag påminna dig om att du trodde att ’rum’ handlade om n st separata ’ affina transformationer’ där du bahövde själva datat för din ’transformation’?
Maken till idioti … men så gick det alls efter att du gröttmyndigt ville berätta om att i ditt ’matematiska universeumä spelade det minsann ingen roll, alla datamängder kunde transformeras åt godtyckligt håll.
Som sagt. ’Medelvärden’ är nog din nivå, börjar dom ’rulla’ så blir det svårt. Och som sagt, du har nu haft massor av ggr på dig att besvara tex #92. Men du behöver inte. Precis lika lite som alla förra gånger du försöt utmana finns det ngt vetttigt du kan svara …. Istället blir det Björnes vanliga aptjatter.
Där han försöker intala sig att ’rullande medelvärden’ är ngt så avancerat att det gör ’matematik till hans faktiskt starkaste sida’. Vilken tönt ….
Christopher ang #91.
Nu är jag emot dödsstraff eller dylikt för rent oförstånd, men ett annat ännu mer träffande citat är:
”If, in a moment of insanity, you do smooth time series data and you do use it as input to other analyses, you dramatically increase the probability of fooling yourself!”
Jonas N vevar och fäktar desperat och fortsätter att stapla ad hominem påstående men han visste inte ens vad ett rullande medelvärde var. 🙂
Eller affin transformation för den delen. Du trodde det var en linjär transformation…. 🙂
Och sedan blev du grön av avundsjuka när jag visade hur man kunde göra om en affin transformation till en linjär. På två olika sätt dessutom. En icke-inverterbara och en inverterbar. JonasN kom aldrig längre än till ett olösbart ekvationssystem.
Staaaackars Jonas N. Han vill så mycket men så fel det blir! 🙂
Fel på alla punkter, din tönt. Du kan fortfarande inte göra det som jag påpekade redan innan ditt infantila inhopp att det inte gick. Dvs invertera och hitta tillbaks till urpsurngsdata utan att spara undan (information om) det.
Och mängden stollefel du travade på varann medans du försökte likande ingenting. Och du vet fortfarande inte vad den affin transformation är heller. Trots att det var du som googlade fram begreppet. Och trodde att du äntligen hade landat en träff! Men det är klart, om du inte vet vad en transformation av ett rum (R^n) är så vet du heller inte vad en affin transforation är …
Det måste svida rejäly. Du håller ju fortfarande fast vid dårsvamlet! Hur länge sen är det nu? Dryga året? Vilken loser ….
Och enligt egen utsago är matematik din starkaste sida!? 🙂 Tja, den delen skulle ju tom kunna vara sann. Du kan ju medelvärden, men vet inte varför släpande medelvärden inte är några medelvärden i egentlig mening …
Vet du ännu vad du ville visa med dina släpande medelvärden och styckevisa trendanpassningar i #18?
Jag kan tala om det för dig, för du lär aldrig komma längre. Du ville ordbajsa lite och diarrédumpa …
Som sagt Björne, du är inte den vassaste träsleven i lådan. Men frågan är om det verkligen kan vara så illa som du själv beskriver dig här. Alltså att du tror all den dynga du kläcker ur dig. Den välvilliga tolkningen är att så j_vla illa kan det inte vara. Utan att du skriver dynga och osanningar för att skyla över hur lite substans du har att komma med, och likaledes för att skyla över alla praktsjälvmål du redan har levererat, och dem har du nog levererat i helt ärlig ignorans och fatal okunskap …
I frågan som du nu försökt historierevidera i över ett år var det din utsaga om att ’i det (Björnes) matematiska universum kan man transformera alla data sett åt båda hållen, att det är gödtyckligt vilket man börjar med, och att varje algoritm var inverterbar’ …
Du ett drygt år senare har du till slut förstått (efter mycket tålmodig hjälp, från fler än mig) att detta är fel, och dvs att faktiskt måste spara (Viss) data. Men är fortfarande i förnekelse om att allt du säger är att du (fortfarande) måste spara din fusklapp. Du kallar det nu (återigen totalt felaktigt) ’en inverterbar transformation’ men allt du hade gjort var att skriva in fusklappen i matrisen (dvs göra din ’transformation’ beroende av var i rummet du befinner dig, dvs ingen transformation) och dessutom lägga till en totalt meningslös rad som väsentligen sa att 1*1=1.
Och nu hävdar du att du kan göra om en linjär till en affin transformation.
Det finns visst ingen ände alls på vilka idiotier du kan försöka med för att skylla över att du är en tafflig slarvig inkompetent amatör när det kommer även till enklare matte …
Staaaackars JonasN.
Fullstädigt demolerad när jag visade på en invers linjär transformation som gjorde mätdtata till anomalidata och tillbaka. 🙂
https://www.klimatupplysningen.se/2013/09/22/climate-glasnost/ #164 och framåt.
Och nu, #69 där han bevisar att han inte ens vet vad ett rullande medelvärde är.
Staaaaackars JonasN.
Vi kan ju test ditt dyngdravel direkt:
Här är anomalidata (bara 2 värden, dvs R2): [-1 1]
Sätt igång och invertera!
Det är klart att du inte kan Björne! Trots allt ditt aptjatter har du aldrig levererat ngt av värde. Nada! Zilch!
VIlken j_väla loser du är BjörneT.
Ett år har gått och du försöker fortfarande kämpa ned verkligheten mot allt vetande och förstånd.
Det är bra att du faktiskt (nästan) länkade en av dina värre sstolle kommentarer. Nästan allt du skriver där är totalt matematiskt nonsens. Och det du tror är ’din stora bedrift’ är att du gömmer medelvärdet M i det du felaktigt kallar ’transformationsmatris’ vilket visar att du är totalt väck rörande även det mest basala i diskussionen. Totalt jävla väck!
Om du fortfaranda tror (och hederligt, på allvar tror) att det du levererade i #164 har ngt värde, eller vore ngt nytt, är du i sanng att beklaga. Men å andra sidan. Jag vet ju att du är en patologisk mytoman. Så eventuellt ljuger du bara ännu mer för att slippa hantera hur fullständigt väck du visade dig vara …
Tack för att du tog fram den trden igen. Den innehåller massor av Björne-guldkorn!
😉
Önskar att jag kunde säga Nice Try.
Men det är bara rent trams.
Vad adderar du för två tal för att få 17 JonasN?
Men i länken ovan beskriver jag EN invers matrisoperation som förvandlar en godtycklig mängd mätdata till anomalidata och tvärtom och jag jag kreerade den dessutom medan du ställer infantila frågor likt de i #107.
Staaaaaaackas Jonas. Den misslyckade matematikern som inte kommit längre än till olösbara ekvationssystem och ställa frågor i stil med vad ska man addera för två tal för att få 17. Och ständigt snubblar på 2×2-matriser och inte ens klarade att räknade ut hur långt man kan se från Kebnekajses topp trots att han googlat fram formeln, som jag tog fram i huvudet i ett fjälltält utan ens papper och penna.
Och inte ens vet vad ett rullande medelvärde är. #69 i denna tråd.
Hur skall du ha det? Hade du en inverterbar transformation eller hade du det inte, BjörneT?
Svaret är att du inte hade det. Alla dina påståenden om motsatsen, nyss i #103, har varit samma Björne-bludder som nästan allt du försökt med! Och nu tom i #109.
Men du kan ju inte ens invertera anomalierna [-1 1] !
Nej du din fjant, dp var din ursprungliga metod faktiskt bra mycket bättre, och faktiskt helt korrekt: Du sparade medelvärdet M på en lapp, och ifall någon talade om för dig exakt från vilken uppsättning mätdata du hade beräknat dina anomalier, då kunde du plocka fram lappen igen, och lägga till M till var och en av dessa.
Den beskrivningen är faktiskt helt korrekt, matematiskt. Och såger ju explicit att du inte kan invertera datamängden: Du behöver veta till vilken uppsättning mätdata du vill hitta tillbaks.
Det är helt sant att du kan skriva upp ditt medelvärde M i en matris. Men då behöver du en matris för varendaste punkte i hela rummet R^n! Och det är många punkter, skall du veta. Oändligt många!
Så nej, du är fortfarande kvar vid samma gamla fusklapp, och har bara försökt ge den nya kreativa och (ev) mer komplicerade namn. Dvs du år fortfarande kvar precis där du började, och där dina försök till utmaningar ledde till formidabla magplaskskavalkader. Vilka du tycks upprepa om och om igen, tom nu!
Som sagt, din största bedrift verkar ha varit att noterat ett teckenfel i ett ekvationsysystem efter att jag skrivit ut det korrekt iaf fyra ggr tidigare åt dig. Det är din nivå Björne. OCh du påstod att du hade klarat av en huvudräkning i ett tält en gång. Men när jag gav dig exakt samma funktionella formen, behövde du 15 timmar på att bekräfta att du hade gått tillväga likadant. Jag vet inte om du kallar sådant för en ’bedrift’ men inte imponerar det på någon direkt … speciellt inte med din mycket långa och omfattande historik av historierevisionism och ren mtyomani.
En annan sak, om du nu klarade av att göra en enkel beräkning i huvudet och bara ta med den dominerande termen, varför är du då so erbarmligt dålig idag på att greppa ens de mest elementära sammanhangen. Du har ju tom skrävlat om att du läst mycket mer matematik sedan dess!?
Jag gissar att du inte förstod så värst mycket av vad du läst, klarade tentan på någora enkla typtal (eller ni kanske inte ens behövde tenta där du ’läste’? Det kanske räkte med ’inlämningsuppgifter’?) Skit samma …
Hur som helst, varför skulle någon ägna över ett år åt att krångligt beskriva hur den vill spara och gömma undan oändligt många fusklappar för att i teorin, dvs om han dessutom får veta till vilket urpsrungligt dataset varje enskild av dessa (oändligt många) fusklappar leder till av någon annan …
Varför skulle någon idiot hålla på med att ’argumentera’ sånt, när han redan från böran informerades om att den sortens (anomali-) beräkningar inte går att invertera tillbaks. Och att det är fullständigt trivialt att inse detta.
Kanske för att det fortfarande inte är trivialt att inse detta för somliga. Nyss försökte han ju stödda sig om hur kreativt han hade skapat sina inverternara ’transformationer’ bara för att än en gång stupa på det banala exemplet [-1 1].
Angående dina ’rullande medelvärde’ hade du fått en specifik fråga och uppmaning. Du har inte kommit med ngt alls där heller. Bara upprepat hjärndött aptjatter … eller kanske desperat kontrafaktiskt önsketänkande, som ju varit centralt i ditt MO även förut.
Men OK, prova en gång till att ’transformera’ [-1 1] till de mätdata dessa anomalier härleddes från. Du var ju ’grön av beundran’ inför din egen förmåga alldeles nyss. 😉
Allt ditt ordbajsanade Jonas N kan inte dölja att du är en misslyckad stackare inom matematikens värld. Du kanske är duktig på annat? Ägna dig åt det då!
Dina löjliga frågor till mig om att ta fram mätdata från anomalidata avslöjar dig totalt! Denna fråga som du ställde precis i början av vår ”diskussion” (du pladdrar, jag kommer med matematik) och sedan som ett litet barn (Staaaaaackars Jonas) upprepat gång på gång i tron att det är någon slags matematik du utövar, har jag otaliga gånger svarat på, att det inte går.
Men i https://www.klimatupplysningen.se/2013/09/22/climate-glasnost/ #164 och framåt visar jag hur man går från mätdata till anomalidata och tillbaka med hjälp av en inverterbar matrisoperation och för att komma till det visade jag hur jag gick från n affina transformationer till en affin transformationi n-rummet som jag sedan gjorde om till en inverterbar linjär transformation i n+1 rummet. Något du först bara kunde gapa åt, och sedan använde 100 inlägg till att försöka trivialisera.
Lägg till det att jag tidigare även tog fram matrisen med vilken man linjärt(men ej inverterbart) transformerar n mätdata till n anomalidata medan du lallade med ditt olösbara ekvationssystem så har det hela i ett nötskal.
Du din stackare gapar och fäktar, kommer med frågor du vet inte har något svar och tror att du är slug som gör det,och klipper då och då in nåt framgooglat du tror är formellt korrekt matematik om oändliga punkter fast vi hela tiden diskuterar ett ändligt antal och redan befintliga mätdata.
Träna på din huvudräkning (Kebnekajse visar att det behövs) och studera elegansen i mina linjära transformationer med hjälp av n, respektive n+1 matriser och plugga på vad rullande medelvärden är (#69 avslöjade dig) så kanske du kommer upp till gymnasial kunskapsnivå på din matematik.
Staaaaaackars Jonas.
Jonas N #105 skriver du ”Och nu hävdar du att du kan göra om en linjär till en affin transformation.”
Du har fortfarande inte lärt dig skillnaden,ser jag,trots mitt påpekande att du blandar ihop dem. Vad jag hävdar och visar är att jag göra om en affin transformation till en linjär. På två olika sätt dessutom.
Och staaackars Jonas. Anomalivärde = Mätvärde-Medelvärde (av n-mätvärden) ÄR EN affin transformation i 1-rummet. Något du felaktigt påstår att det inte är.
N sådana affina transformationer kan göras om till EN affin transformation i N-rummet.
Vi får då att en kolumnvektor med anomalidata (med n element) är lika med en kolumnvektor av mätdata (med n element) ggr en nxn matris (som är enhetsmatrisen) plus en translationsvektor med medelvärden (eller summan av alla mätdata delat med n) som också är en kolumnvektor med n element.
Denna affina transformation i n-rummet kan nu göras om till EN linjärtransformation i n+1 rummet vilket jag redogjorde för i https://www.klimatupplysningen.se/2013/09/22/climate-glasnost/ #164 och framåt.
Vi får då att en kolumnvektor med n anomalivärden och ett dummyvärde på 1 är lika med en kolumnvektor med n mätvärden plus ett dummyvärde på 1 ggr en (n+1)x(n+1).matris. Denna matris är enhetsmatrisen utökad med en rad och en kolumn där kolumnen är kolumnvektorn (translationsvektorn) med -mätdata plus 1 och raden är en serie nollor utom sista som är 1. Se #234 i länken ovan,
Opraktiskt med papper och penna (eller räkndedosa) men matematiskt elegant och lämpligt för en dator,något du själv, staaaaackars Jonas, var noga med att påpeka när du började pladdra om transformationer.
Nu har jag alltså EN algoritm med vilken jag går från mätdata till anomalidata. Denna algoritm är dessutom inverterbar för genom att invertera matrisen kan jag använda den att multiplicera anomalidata-vektorn och få tillbaka mätdata-vektorn. Invertera (n+1)x(n+1).matrisen görs genom att ändra minus-tecknet tillplustecken framför den högraste kolumnen utom för sista elementet som ju är 1. (se som ovan #234 där jag illustrerar det hela med exempel).
Inför denna matematiska elegans är allt staaaaaackars Jonas har att komma med är att ge mig två anomalivärden och kräva att jag ska ta fram de ursprungliga mätvärdena, något jag förklarade första gången (av tjogvis) inte gick (eller rättare sagt går att göra på oändligt många sätt. Men staaaaackars Jonas tror att denna banalitet är den tuva som ska stjälpa mitt matematiska lass, men denna tuva är ingen jag ens kör över annat än i staaaaackars Jonas värld. Staaaackars Jonas, du kan peka på den där tuvan i hundra år men jag kör helt enkelt inte den vägen!
Med denna metod kan jag nu obehindrat och med en enda matematisk operation gå från en godtycklig uppsättning mätdata till anomalidata och tvärtom.
Sedan kan staaaackars Jonas för femtielfte gången pladdra om fusklappar, det ändrar inte faktum.
Sedan har jag också visat för staaaaackars Jonas hur man kan gå från en kolumnvektor mätdata till en kolumnvektor anomalidata med en linjär transformation i n-rummet som INTE är inverterbar (Staaaaackars Jonas hade visst kört fast i ett trivialt ekvationssystem) det vill säga en operation som innebär att vi i princip kastar bort mätdatat efter att ha tagit fram anomalidatat.
Således har jag härlett och visat på två olika metoder att göra linjära transformationer på mätdata för att skapa anomalidata, en inverterbar och en icke-inverterbar och allt staaaackars Jonas har gjort är att pladdra och bildligt talat fäkta med armarna. Och komma med förolämpningar förstås men det gör han ju oupphörligen så det bryr jag mig inte om.
PS .Implicit i dessa resonemang är att anomalidatat bildas utifrån medelvärdet av all mätdata.Så behöver ju inte vara fallet men det ändrar ingenting av den matematiska resonemanget.
BjörnT – Du ägnar alldeles för mycket av din (i brist på bättre ord) ’tankemöda’ åt att försöak fantisera fram ’sanningar’ om saker du varken känner till eller behärskar ens hjälpligt, kort sagt åt infantilt önsketänkande, projicerinagr och rent hittepå.
Inte på någon punkt har du fått in ens en ynka liten träff. De felskrivningar, slarv, eller missuppfattingar jag ev har gjort är en mild västanfläkt jämfört med samma (jag utgår från oavsaiktliga) misstag och klavertramp du har begått under samma tid. Där finns öht inten jämförelse.
Men smärre misstag, slarv och dylika ärliga fel är totalt irrelevanta i sammanhanget, sådana förekommer förstås om postar och skriver snabbt, och inte korrelkturläser.
Jag håller inte ens alla dina (många) klantiga misstag emot dig, de flesta har jag inte ens påpekat (utan det är du som hävdar att de skulle bevisa att du är en totalt misslyckad nolla som inte begriper matematik, om man får tro din idiotargumentation som du vill använda åt andra hållet)
Utan det som avslöjar dig är de riktiga, grova, matematiskt totalt ignoranata dikeskörningar som du gjort. Och att de inte är misstag visas av att du upprepar dem många ggr. Vissa av dem fortfaranda. I denna tråd har du levererat ytterligare ett stollemagplask om dina ’transformationer’ som jag inte ens påpekat ännu.
Ledsen där, Björne, men du har så grundligt och så med eftertryck demonstrerat att du inte förstår den matematik ens som lärs ut 1:a året på universitetet. Och du skall veta att du har fått omåttligt mycket hjälp av mig att förstå massor av de saker du missat, glömt, missförstått och inte sällan totalt kvaddat.
Du skriver ovan ngt som du redan har hävdat, som jag redan kommenterat, men missar fortfarande totalt. Totalt Björne! Missar att du inte hr skrivit upp en transformation av ett rum, utan bara konstruerat en avancerad (nåja) fusklapp för att från en punkt i det ena rummet hitta till motsvarande andra. Och ja, åt ena hållet är detta görbart (bör dock göras som jag formulerade det, dvs korrekt och kompakt), men du menar att om du får spara dina (nu ’avancerade’) fusklapp så kan du hitta tillbaks från punkten i det andra rummet till var du startade i det första.
Ja, så kan du göra. Men som jag sa ovan, och du själv sa tidigare, är det mycket mera praktiskt att bara skriva upp M på din fusklapp och( kräva att få veta vilken av alla oändligt många fusklappar du skall använda för att) lägga till M igen.
Att din matris är inverterbar är inte mer konstigt än att ifall du har M så kan du utföra både operationen -M, och sedan +M. För det är ju vad din påstått eleganta kreativa (inverterbara) matris gör. Den gör inget mer! Och ffa är det inte en transformation. Det är en matris som är helt beroende av var i rummet R^n du befinner dig, dvs den transformerar inte ett rum till ett annat. Utan bara en punkt i det ena till motsvarande punkt i det andra. (Nåväl, den gör det faktiskt för alla punkter som uppvisar samma medelvärde, men överiga är fortfa oändligt många ggr fler)
Så nej, du har fortfarande inte åstadkommit ett skvatt. Du har skrivit upp M, sparat det. Och behöver det för att hitta tillbaks! Och du behöver dessutom veta till vilket dataset du vill hitta tillbaks.
Enklet demonstrerat igen:
Du får nu två uppsättningar an anomalier a) [-1 1] och b) [-1 1]. Notera att i anomalirummet R^2 utgör de samma punkt. Men de kom från två olika uppsättningar mätdata. Den ena hade medelvärdet M=3.7, dvs du kan nu kontruera din ’eleganta kreativa inverterbara matris’. Gör det!
Men nu skall du ju ge mig båda uppsättningar mätdata, Björne. Och det kan du inte! För att allt du har snackat har varit blahablaha .. Du kan inte ens hitta tillbaks till en av dessa uppsättningar mätdata (trots att du fick fusklappen M=3.7) av mig.
Det enda du kan göra (mha av min fusklapp, som jag generöst sparat åt dig) är att chansa ifall det är dina beräkningar ger dig urpsr mätdata motsv namonalierna från a) eller b).
Eftersom du fortfarande inte gör ngt annat än att försöka spara en fusklapp och gömma den tillsammans med ’svaret’
Nu fick du svaret [-1 1], och du fick fusklappen M, men fick inte veta om dessa hörde ihop (OK du fick veta att ett av två likanda ’svar’ hör ihop med M). Så du är precis lika väck som förut.
Där finns vare sig ngt elegant, npgot kreativt, eller något matematiskt begåvat eller ens intuitivt värdefullt med ditt nu årslånga pladder.
Du har beskrivit meningslösheter, identiteter, och trams under ett år. Hävdar du motsatsen får du allt bestämma (inte gissa, OBS!) urspr mätdata till ett av fallen a) eller b). Och du behöver förklara hur du gjorde.
Vidare, till skillnad från ditt fjantiga årslånga tramsande och rena aptjattret, behöver jag inte gissa (önsketänka) om din matematiska förmåga. Du har demonstrerat den här (och jo, skrävlat lite om bedrifter som inte går att kontrollera, men tog väldigt lång tid att (ev åter-)upprepa efter att jag hade förklarat hur det går till: Kebnekajse). Därför kan jag utan att minsta bekymmer säga att jag tror att du äger alldeles tillräckligt mycket ’matematisk förmåga’ för att till fullo inse att du med bara ett M omöjligen kan ta fram urspr mätdata till anamalierna i både fall a) och b).
Du inser att du behöver varje M för att hitta tillbaks. Poängen är att du inte ens med M givet kan gå tillbaks till mätdata från anomalier. Nyss demonstrerat med fallen a) och b).
Faktum är att jag kan ge dig alla tänkbara M om du vill. Som alltså hittar tillbaks till hela rummet med urspr mätdata R^n, från hela anomalirummet R^n. Och dessa är: [-∞ ∞] och du kan fortfarande inte hitta tillbaks en enda gång. Annat än om du får antingen skriva upp eller reda på vilken punkt du skall hitta tillbaks till.
Det är så att säga grejen med att icke-inverterbarhet. Och kanske kanske kommer du ihåg att jag redan från allra första början talade om det för dig, och sedan tålamodigt förklarade också.
Sorry Börne, men jag tycker inte att du skall använda ordet ’orbajseri’, inte när det du säger ständigt flyger upp i egna ansiktet …
😉
Staaackars Jonas villar bort sig igen.
Jag har tydligt beskrivit hur n mätdata uppställt i en n-kolumnvektor kan kan multipliceras med en transformationsmatris (n+1)x(n+1) för att skapa en kolumnvektor med n anomalivärden, en linjär transformation.
Genom att ta inversen på transformationsmatrisen kan jag också multiplicera kolumnvektorn av anomalidata och få tillbaka en kolumn med det ursprungliga mätdatat.
Men det där ligger bortom staaaackars Jonas fattningsförmåga.
Alltså, jag repeterar, en, säger en, uppsättning mätdata, kan transformeras med en, säger en, matris och skapa motsvarande uppsättning anomalidata.
Och samma matris men inverterad kan transformera tillbaka anomalidatat till det ursprungliga uppsättningen mätdata.
Staaackars Jonas babbel om oändliga mängder är totalt meningslöst. Det finns EN transformationsmatris för EN uppsättning mätdata för att skapa anomalidata. varken mer eller mindre.
I https://www.klimatupplysningen.se/2013/09/22/climate-glasnost/ #164 förklarar jag hur jag härledde den och i #234 finns ett exempel på en transformationsmatris för två mätdata x1 och x2.
BjörnT
Anomalier är:
a) [-1 1] och
b) [-1 1] ’
Du har tom fått att M=3.7.
Varsågod: Demonstrerar din metod nu!
(Att om du kan räkna M för en uppsättning mätdata, dra ifrån den, och sen lägga till igen är det ingen som ifrågasatt. Att spara den på en fusklapp och tom fästa den på beräknade anomalidata ansåg du ju själv var bästa metod. Varför du nu skall trockla in den i en matris är obegripligt, men matematiskt kan du förstås göra det också. OCh lägga till att 1*1=1 i en extra rad tex. Rätt! Men förstås meningslöst.Varför upprepar du meningslösheter som du tom fått bekräftade av mig att vara korrket uppställda?)
Notera att du dock inte håller på med transformationer mellan rum. Din matris är nu beroende av mätdata, dvs annorlunda för andra punkter i rummet. Det är inte en linjär transformation längre Björne! Din matris är inte längre konstant utan beror av X.
Notera också att även detta har jag talat om för dig massor av ggr.
Men som du säger: Det är tydligt långt över din fattningsförmåga, Björne. Du har ju onekligen haft lång tid på dig, och fått oändligt tålamodig hjälp med att få detta förklarat. Och du har ju själv googlat också. Tom hittat ett nytt ord som du trodde var viktigt …
Angående ditt nästsista stycke: Du har fel igen, det du beskriver är en (OK, krånlig) fusklapp.
Korrekt uppställt är sambandet:
Y = A * X + B där B = 0 för anamoaliberäkningar. Och A är oberoende av mätvärdena. Som jag alltså sa från allra första början. Och jag förklarade också varför du misslyckas med uppgiften högst upp i denna kommentar: Det har med A:s egenskaper att göra.
Och A (resp ett ev B) är konstanter. Oberoende av exakt vilken punkt (mätvärden) du vill transformera. Som jag sa till dig från allra första början!
Ledsen Björn, det är fortfarande så att allt jag talat om för dig varit korrekt, och varje gång du säger emot mig har du (haft) fel. Slarvfel får du gläjda dig åt, men ändrar nada …
Jonas N: Om du har en två uppsättningar anomalier, -1 och 1 och medelvärdet för en av dom är 3,7 så är mätvärdena för den 4,7 och 2,7 givetvis.
Vi har de två affina transformationerna
1 = 4,7 -3,7
-1 = 2,7-3,7
och detta kan vi göra om till en linjär transformation:
|1 | |1 0 -3,7| |4,7|
|-1| = |0 1 -3,7| *|2,7|
|1 | |0 0 1 | |1 |
Där sista elementet i kolumnvektorerna liksom sista raden i matrisen är dummy-värden.
Vi kan alltså göra om mätvärdena 4,7 och 2,7 till anomalierna 1 och -1 med en linjär matristransformation och vi kan återskapa mätdata från anomalidatat genom den inversa -matrisen som ser likadan ut frånsett att vi ändrat – till +.
Alltså, EN uppsättning mätdatat har EN matris som kan skapa EN uppsättning anomalidata och genom att invertera matrisen kan vi transformera tillbaka anomalidata till mätdata.
Här behövs inga fusklappar, om du inte några fusklappar och inga oändliga mängder som du förvirrat babblar om!
QED.
Tillägg till #116.Jag behöver inte ens veta, eller räkna ut medelvärdet för en given uppsättning mätdata. I min matris kan jag skriva den högra termen som -(4,7+2,7)/2, dvs bara använda mig av mätdatat.
Formidalbelt!
Notera att Björnes stora (eleganta kreativa begåvade ) poäng är att han kan transformera tillbaks till mätdata [x1 x2] från motsv anomalidata [y1 y2]. Att han tror sig skapat en ’inverterbar transformation’.
Hans inlägg #234 (i ovan länkade tråden) lyder i sin helhet:
Komplettering #164 och#200.
I posterna ovan visar jag på en 3×3 matris som tar två mätdata, x1 och x2, till anomalidata plus ett dummy värde på 1.
Matrisen ser ut såhär:
1 0 -(x1+x2)/2
0 1 -(x1+x2)/2
0 0 1
Jag har gruvat mig för att ta fram inversen av det för att ta anomalidata till mätdata, normalt en väldigt jobbig procedur, men insåg plötsligt!!!:
Inversen är helt enkelt bara:
1 0 (x1+x2)/2
0 1 (x1+x2)/2
0 0 1
Dvs värdena i kolumnen längst till höger (den vi stoppat in i en enhetsmatris) ska helt enkelt ändra tecken utom för sista posten!
Fucking briljant!
JonasN: Matematisk intuition i arbete!
Slut citat!
Som sagt, helt formidablet!
Dels skriver han rätt ut att han behöver alla sina mätvärden i det han (felaktigt) kallar transformationsmatris, inskrivna där i form av sitt medelvärde M. Och denna matris (inkl M) behöver han alltså för att hitta tillbaks till precis samma mätvärden. Dels tycks han inte inse att han inte gör ngt annat än att anomaliberäkningar inte gör ngt annat än att dra ifrån det medelvärdet från varje mätvärde. Mendessutom blir han uppriktigt förvånad över att ’hans nu inverterbara matris’, när man skall gå åt andra hållet inte gör ngt annat än att åter lägga till samma medelvärde, dvs att han byter tecken på den termen. (Och ja, jag har fortfarande en meningslös rad som säger 1*1=1 med på slutet. Men även den är ju rätt)
Även fortsättningen av diskussionen är lika formidabel. Han får nämligen dessa säjlvklarheter påpekade omedelbart! Se tex #235, #236#236 och ffa #237.
Som sagt, det är synd om mänskligheten … iaf vissa av dem
BjörnT #116
Japp, om anomalidata är [-1 1] och tillhörande M=3.7 så blir det som du säger.
Men det var inte uppgiften (jag vet att du klarar av matematik på den nivån). Uppgiften gällde istället ifall du har två uppsättningar mätdata, och mha dessa beräknat två uppsättningar anomalidata:
a) [-1 1] och
b) [-1 1] ‘
Samt att du dessutom får veta att fusklappen sa att M=3.7 som hörde till anomalidatat [-1 1].
Frågan var om du nu kan beräkna mätdata till anamalier i fall a) resp i fall b).
Hela din självgoda präktighet här handlade ju om att du kan gå åt båda hållen. Men (och ifall du inte vet/förstår det så) behöver du hantera att i anomalyrymden (R*2) är [-1 1] en enda punkt.
Hur transformerar du tillbaka till mätvärdes rymden [x1 x2]?
När du nu vet att olika uppsättningar mätvärden kan ge samma anomalier [-1 1]! Hur gör du då?
(#116, användgärna inte begreppet ’affina’ och helst inte ’transformation’ heller. Det du beskriver i början av #116 kallas ’subatraktion’, dessutom subtraktion av ett medelvärde som är helt bestämt (beroende) av vilka punkter du vill ’transformera’. Om du inte förstår det själv, så tro mig på den punkten. Som du vet behöver jag inte ljuga om saker och ting)
Jonas N.Tröttnar du aldrig på att fjanta dig? Då frågar gång på gång ekvivalensen av vilka två tala har jag adderat för att få 17. Som jag har sagt tusen gånger. Den här gången gjorde du exakt samma sak och du tror förmodligen att du är listig,
Och läs på om transformationsmatriser du verkar totalt okunnig inom området!
Affine transformations[edit]
To represent affine transformations with matrices, we can use homogeneous coordinates. This means representing a 2-vector (x, y) as a 3-vector (x, y, 1), and similarly for higher dimensions. Using this system, translation can be expressed with matrix multiplication. The functional form x’ = x + t_x; y’ = y + t_y becomes:
\begin{bmatrix} x’ \\ y’ \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}.
All ordinary linear transformations are included in the set of affine transformations, and can be described as a simplified form of affine transformations. Therefore, any linear transformation can be also represented by a general transformation matrix. The latter is obtained by expanding the corresponding linear transformation matrix by one row and column, filling the extra space with zeros except for the lower-right corner, which must be set to 1.
På länken http://en.wikipedia.org/wiki/Transformation_matrix syns matrisen men jag har gjort det bekvämt för dig:
http://www.bilddump.se/bilder/20140112211514-83.233.174.89.JPG
Som sagt JonasN…
I #116 Gör jag exakt denna affina transformation med en transformationsmatris
http://www.bilddump.se/bilder/20140112211514-83.233.174.89.JPG
som jag härleder här t.ex. (från #116):
Vi har de två affina transformationerna
1 = 4,7 -3,7
-1 = 2,7-3,7
och detta kan vi göra om till en linjär transformation:
|1 | |1 0 -3,7| |4,7|
|-1| = |0 1 -3,7| * |2,7|
|1 | |0 0 1 | |1 |
Och notera att jag själv tog fram denna transformationsmatris något du försöker förringa med ditt svammel ovan.
Som sagt, jag skapar matematik du babblar och fäktar med armarna.
Jonas i #120
”(#116, användgärna inte begreppet ‘affina’ och helst inte ‘transformation’ heller. Det du beskriver i början av #116 kallas ‘subatraktion’”
Jaså,det säger du:
”When children find the answers to sums such as 4 + 3 or 4 − 2 by counting right or left on a number line, they are treating the number line as a one-dimensional affine space”
http://en.wikipedia.org/wiki/Affine_space
Som sagt, du gör dig enbart till åtlöje Jonas.
BjörnT
Du har hållit på i över ett år och fäktat och skränat och slagit in dörrar som andra hållit vidöppna åt dig. Tröttnar du aldrig? Varför inte ägna den energin åt att lära dig lite mer om grundläggande matematik där det hos dig fortfarande finns stora brister.
Och nej, jag har inte frågat om vilka två tal som ger summa = 17. Även om beräknandet av mätdata från anaomalidata innehåller samma svårighet (dvs icke-inverterbarhet hos algoritmen). Notera att mätdata och anomalidata alltid har lika många värden. Dvs att man avbildar R^n på R^n (vilket inte är fallet för exemplet ’vilka n tal ger summan 17’)
Du länkar sen till en wikipedia-artikel som nog är långt över ditt huvud. Men framför allt avser den delen du kopierar in en translation av koordinatsystemet med [tx ty]. Den beskriver att en affin transformation (tex en translation) kan skrivas om till en matrismultiplikation (mha en dummyvariabel 1).
Vilket dock är ngt helt annat än vad du hållit på med nu i över ett år:
1) Du vill göra denna translation beroende av position, nämligen beroende av vektorn [x1 x2] (eller möjl [x1 x2 1] i din misslyckade omskrivning).
Så är det inte! Och
2) Anomaliberäkningar är ingen translation. Nollan avbildas på nollan, dvs om alla mätvärden är noll så blir även anomalierna samma.
Problemet du har (och som jag påpekat i över ett år) är att även om alla mätvärden tex är 3.7 C blir anomalierna nollan. Dvs icke-inverterbarhet!
Så är det!
tx och ty är konstanter i din wikilänk, och det som står där är korrekt. Det du försöker är (matematiskt) också korrekt, men har inget med wikilänken att göra, du försöker göra tx och ty beroedne av x1 och x2. Det är ngt helt annat. Släpp det nu!
Notera också att jag sedan ~ett år har sagt till dig just det: att du inte får smyga in kooridnaterna x1 x2 (mfl ev) i dina ’transformationsmatriser’. Dvs att jag redan innan du begick felet i #121 om och och om igen manat dig till att inte göra det! Släpp det nu för guds skull!
Ledsen, men ovanstående wikilänk i #121 är ännu ett rejält magplask från dig, Dvs demonstration av att du inte behärskar det du försöker dryga dig om. Även denna gången oprovocerat. Möjligen kan jag bjuda på viss straffrabbat iom att det bara var samma feltänk du har försökt många ggr förut, nu denna gången hänvisandes till ( och felaktigt i tron om ngt) stöd från en wiki-länk.
Vi är fortfarande kvar vid att du omöjligen kan invertera anomalidata [-1 1] även om jag talar om för dig att där funnits ett tillfälle där dessa tagits fram mha medelvärde M=3.7.
Vilket förstås har varit sant hela tiden, och jag sagt redan långt innan du hoppade in. Och förklarat många ggr därefter för dig!
Björne #122 och #123
Du lyckades med fler magplask medans jagskrev #124
Om du hade definierat Björne-skalan på mätvärdena, alltså att Björne-värden är mätvärden (tex i SI-enheter) minus 3.7 (i samma enhet) så hade du faktiskt haft rätt. Då hade det varit en affin transformation, där i den korrekta skriviningen Y = A*X + B man hade haft B=[-3.7 -3.7], då hade allt i #122 stämt och varit korrekt.
Problemet är forfrande att anomalier inte är ngn påhittade Björneskala, där man alltid drar ifrån 3.7. Det är i stället en mycket väldefinierad linjär transformation, där tom du själv till slut lyckades skriva upp den allmäna formlen (helt utan att blanda in ett enda mätvärde, remember?). Och händelsevis en transformation som inte går att invertera. Vilket jag talade om för dig redan när du började mopsa dig om ’ditt matematiska universom där det är arbiträrt vilket man set man börjar med, där alla algoritmer är inverterbara’.
Du är forftarande kvar vid att försöka rädda ansiktet från det. Och misslyckas kapitalt förstås. Men även gör ännu fler magplask med matematik från på wikipedianivå …
Varför tror du att jag tycker det är så kul att hålla dig igång Björne?
😉
Staaaackars JonasN: Jag tror inte du tycker det är ett dugg kul. Du är demolerad och det vet du Var och en kan ju läsa detta:
All ordinary linear transformations are included in the set of affine transformations, and can be described as a simplified form of affine transformations. Therefore, any linear transformation can be also represented by a general transformation matrix. The latter is obtained by expanding the corresponding linear transformation matrix by one row and column, filling the extra space with zeros except for the lower-right corner, which must be set to 1
från wikilänken ovan och se att jag har rätt och att jag har haft rätt i hela tiden,hur du än babblar, fäktar, förolämpar mig och försöker fylla dina inlägg med meningslöst pladder som du tror rättare (hoppas att någon tror) är initierade matematiska resonemang.
Mina resonemang är både korrekta och kreativa och har varit det från början till slut.
Jag har både härlett och demonstrerat inte mindre än två sätt att förvandlat mätdata till anomalidata och för ett av sätten kan man även ta fram mätdata från anomalidata med hjälp av en inverterbar transformationsmatris som jag väldigt kreativt resonerade fram och du desperat försöker trivialisera.
#117
Bra Björne. Nästan rätt. Eller iaf till hälften rätt. Och andra hälften lika fel.
Du behöver bara skriva in mätdatats medelvärde -(4.7 + 2.7)/2 i din matris. Det är inte alls ngn fusklapp med medelvärdet insmuget i din ’inverterbara’ matris! Eller jo, det är ju precis vad det är!
🙂
Men tack för att du skriver ut så tydligt precis det jag mfl har påpekat från allra första början!
Björne #126
Jag gissade att du inte alls hade kommit på din ’augumented matrix’ med en extra dummyrad själv. Nu länkar du till wikisidan där du fått detta ifrån.
Och i ditt svar undviker du (precis som alla ggr tidigare) själva sakinnehållet.
Skftiningen med [tx ty] är en konstant translation. Dvs ngt helt annat än du försöker!
Som jag sa åt dig, släpp både ’affina’ och ’transformationer’, de är långt över ditt huvud.
Du är fortfarande kvar vid att du behöver din fusklapp. Vilket förstås är både sant, uppenbart, och ffa talades om för dig från allra första början! Du har inte kommit en enda millimeter framåt under ett helt år. Annat än att gång på gång avslöja hur lite du begriper av de begrepp du vill slänga dig med, men inte klarar av att använda korrekt!
Bara betänkt det faktum att du hela tiden pratar om ’att omvandla mätdata till anomalidata’ som aldrig aldrig någonsin varit ett bekymmer. Sent omsider lyckades du ju själv formulera den ’allmäna formeln’ som gör detta på matrisform.
Hela tiden har allt (allt!) handlat om att du inte kan gå åt andra hållet. Vilket du inte kan. Vilket du inte ens kan om du får spara din fusklapp i en matrisk. Eftersom du inte vet vilken fusklapp som hör till vilket set av anomalier. Eftersom identiska anomalidata kan komma från många olika mätresultat! Vilket omtalades för dig från allra förstsa början!
Vet du, att du är lite sen med att fatta saker håller jag inte ens emot dig. De flesta studenter kommer inte över din nivå. Men det patetiska (coh beklämmande) är att du tror att de saker du inte begriper gör dig till ngn överdängare i matte. Det är i sanning pisnamt (för dig).
På precis varenda punkt har jag har sagt som det är till dig från början. OCh du kämpar fortfarande emot det faktum … Som sagt, jag misstänker där ligger ngt annat bakom!
🙂
Staaaackars Jonas.
”Släpp både affina och transformationer”.
Jojo, i länkarna ovan bevisar att jag har rätt och du har fel m.a.p. dessa termer. Jag använder dem korrekt och du håller på med meningslöst pladder.
Och du vet mkt väl att jag egenhändigt snickrat ihop inte mindre än två matriser som kan användas till att via linjära transformationer (matrismultiplikation av en kolumnvektor) göra anomalidata av mätdata och i ett av fallen göra mätdata av anomalidata, oavsett om du kallar den matrisen fusklapp eller inte.
Givetvis kan man inte enbart från anomalidata återskapa mätdata något jag aldrig hävdat fast du tjatar om att jag ska göra det som en berusad papegoja.
Jag har tagit fram en algoritm i form av en inverterbar matris som gör jobbet att både skapa anomalidata av mätdata och vice versa på ett matematiskt mycket elegant sätt oaktat dina försök att förringa det hela,kalla det fusklapp och påstå att jag behöver oändligt vilket är rent BS.
Jag behöver exakt EN sådan matris för varje uppsättning mätdata.och den skapas enbart av mätdata med en känd algoritm så det är en allmängiltig metod.
Jag vet inte riktigt hur man skall tilltala en person som verkar ha för gott om vokaler i tangentbordet.
Kanske så här:
Snääääääääääääääääääääääääääääääla Björn T! Lägg ner! Ge dig! Gör något av ditt liv!
Snäääääääääääääääääääääääääääääääääääääääääääääääääääla!
Japp Björne
Du behöver exakt en sådan (n+1)*(n+1)-matris för varje en av (oändligt) många uppsättningar av n mätdata för att hitta tillbaks till dessa. Men du behöver dessutom fästa den informationen vid (oändligt) många versioner av samma anoalidata, och dessutom veta exakt vilken av (oändligt många möjliga) mätdata du faktiskt vill hitta tillbaks till. Dvs du behöver spara oändligt mycket faktiskt data för att hitta tillbaks till precis samma data mha beräknad anomalidata. Dvs du har åstadkommit precis zilch!
Och du har på vägen behövt missbruka massor av matematiska grundbegrepp. För att åstadkomma precis ingenting! Som du själv beskriver som matematiskt elegant, kreativt osv.
Och du har aldrig hävdat att från anomalidata kan återskapa mätdatat trots att du hävdat att i ditt universum är det egalt vilken uppsättninfg data man börjar med. Tom att varje algoritm kan inverteras. I så fall tom alla algoritmer som ger slutsumman 17 (vilket dock aldrig varit på tapeten här)
I princip säger du nu det jag sa för redan över ett år sedan; Att du behlver spara (info om) mätdatat för att hitta tillbaks till det. Dvs att du utan sådan inte har en susning om vad mätdatat var. Konstigt barar att du anser det vara en bedrift att bekräfta vad jag sa till dig från början.
…
Men du verkar vara en märklig person i sådanan avseenden. OCh oförmögen att hantera även enkel matematik
Jonas-babbel:
”Du behöver exakt en sådan (n+1)*(n+1)-matris för varje en av (oändligt) många uppsättningar av n mätdata för att hitta tillbaks till dessa. Men du behöver dessutom fästa den informationen vid (oändligt) många versioner av samma anoalidata, och dessutom veta exakt vilken av (oändligt många möjliga) mätdata du faktiskt vill hitta tillbaks till. Dvs du behöver spara oändligt mycket faktiskt data för att hitta tillbaks till precis samma data mha beräknad anomalidata. Dvs du har åstadkommit precis zilch!”
Jag behöver exakt ett matematiskt objekt,min (n+1)x(n+1)-matris för varje mätserie om n element för att skapa anomalidata av mätdata och mätdata av anomalidata med exakt en matematisk operation.
Och detta matematiska objekt skapas genom algoritm av mätdatat själv.
Och metoden är att av n affina transformationer (där mätdata transformeras till anomalidata) gör jag en affin transformation som sedan görs till en linjär transformation genom en transformationsmatris med n+1 rader och n+1 kolumner.
Elegant och kreativt hur än Jonas babblar och fäktar med armarna.
Jonas har ju naturligtvis ett rätt i trivial mening. OM man samlar in en massa mätdata till stor kostnad och stort besvär och skapar anomalidata av det och därefter KASTAR bort all mätdata och INTE skapar min transformationsmatris DÅ, men bara DÅ,kan man inte hitta tillbaka från anomalidata till mätdata.
Denna trivialitet har jag aldrig förnekat, jag har tvärtom explicit påpekat det omedelbart frågan kommer upp (annars kan ni vara säkra på att Jonas skulle länka till det om jag skulle påstått något annat).
Hur ofta kastar folk bort sina mätdata efter att ha skapa anomalidata tror ni?
Och all matematik och matematisk terminologi jag använt har varit korrekt om än ett och annat slarvfel kan ha smugit sig in. Länkarna till wikipedia ovan bevisar det för den som orkar kolla, vilket Jonas räkna med att de flesta inte orkar.
Dessutom har jag härlett och konstruerat transformationsmatrisen ovan liksom en annan som inte är inverterbar men som också går att använda för att ta fram anomalidata.
Ursäkta att jag lägger mig i, men jag har följt era diskussioner med stort nöje det senaste året. Tack för underhållningen. 🙂
Jag tror att jag hängt med från början, och om jag inte minns fel så började diskussionen med att BjörnT hävdade att han kunde återskapa mätdata från anomalidata. Jonas N sade att det inte går, och sedan har det brakat på.
Nu skriver BjörnT :
”Givetvis kan man inte enbart från anomalidata återskapa mätdata något jag aldrig hävdat fast du tjatar om att jag ska göra det som en berusad papegoja.”
Detta skiljer sig ganska rejält från vad han hävdade förut, och vad jag tror diskussionen egentligen handlar om:
”Vi KAN alltså med denna linjära transformation återskapa mätvärdena från anomalivärdena!”
(https://www.klimatupplysningen.se/2013/09/22/climate-glasnost/#comment-348860)
Menar du att Jonas N haft rätt hela tiden? Eller missförstår jag dig?
133. Du missförstår. Läs min #12.
Jonas N. #128, He he….nu erkänner du indirekt att jag gjorde en elegant härledning på ett en kreativ ingivelse. Kul att du studerade wikipediasidan som jag hittade igår, då kan du ju se hur fel du har.
PS. Det har hänt ett antal gånger att jag tagit fram lösningar som jag behövt i mitt arbete men inte visste att andra gjort långt före mig. Exempelvis sitter jag just nu och gör energisgnaturer, en metod jag tog konstruerade för ett par år sedan helt självständigt men som det sedan visade sig var en etablerad metod.
Björne-T
Det är du som svamlar. Du behöver skriva in mätdata i din matris (i form av M) för att bestämma samma mätdata utifrån anomalier. Det är fortfarande inget annat än din fusklapp. Och som du nu skriver själv behöver du exakt en sådan fusklapp för varenda en (av oändligt många) uppsättnngar mätreslutat. Du säger helt korrekt att om du har mätresultaten så kan du enkelt beräkna denna som en enkel matematisk operation (icke-inverterbar, märk väl), och sedan om du vill (det är ej nödvändigt) skriva om anomalibeärkningar som en matrisoperation, där alltså matrisen är beroende av datat. Som du säger: En matris för varje set mätdata.
Men du kan fortfarande inte hitta tillbaks vilket enkelt demonstrerades av två uppsättningar anomalier:
a) [-1 1] och
b) [-1 1]
som kommer från olika mätresultat. Och en av dem hade medelvärdet M=3.7. Dvs inte ens med din matris (eller sparad fusklapp) kan du invertera beräkningen.
Du behöver dessutom ha det fastklistrat vid själva anomalidatat. Visst du kan klistra fast en (n+1*(n+1)-matris vid dina n anomalier. Jag tycker dock, och du själv höll med tidigare, att det är enklare att bifoga bara M, dvs ett (1) värde så att man kan återskapa mätresultaten.
Men nej, du har gjort groteskt många matematiska fel, en del riktigt rejält grova. Många helt oprovocerade och några av dem upprepade i olika skepnader. Det hela började dock med (precis som Daniel F påpekar) att du hävdade:
” Ingen av data uppsättningarna har någon annorlunda position i det matematiska universumet, det är helt arbiträrt vilket man betraktar som primärt eller deriverat”
PS I denna tråd har du gjort ytterligare ett magplask, när du trodde att det du gör är vad som beskrivs i din wikipedialänk DS
Björne #135
Där behöver inte erkännas något alls, käre Björne. Att du behöver din fusklapp talades om för dig redan från allra första början. Att du nu vill göra samma sak på ett extra krångligt sätt kanske beror på att du vill skyla över alla dina katastrofala dikeskörningar på vägen. Jag har redan sagt att du kan skriva upp din fukslapp på detta krångliga (n+1)*(n+1)-stora sätt. Däremot är det fortfarande inte frågan om någon affin transformation som du gjort om till en linjär. Jag har ju sagt till dig att du helst skall sluta dilla om sådant … det är långt över ditt huvud.
Jonas babblar på helt desperat efter att ha blivit överbevisad om hut fel han har (länkarna ovan) och hur rätt jag har.
Och med min (n+1)x(n+1)-transformationsmatris vandrar jag obehindrat mellan mätdata och anomalidata och tillbaka, något jag hela tiden sagt är möjligt (om man inte kastar bort den liksom mätdatat), den Jonas nu anklagat för att vara samtidigt vara trivial, felaktig och stulen från Wikipedia. 🙂
Sanningen är att Jonas babblar så desperat för han vill dölja att jag bevisat vad jag sagt hela tiden.
Antag att jag har 8 och får mer så det blir 17.Då vet jag att ökningen är 9. Antag att jag har 17 och minskar med 9, då vet jag att jag får 8. Jag kan vandra obehindrat mellan 8 och 17 om jag har 9 och ett av 8 eller 17.
Det den lallande babbel-gubben Jonas ber mig göra är att tala om vad jag hade om jg nu har 18 samtidgt som jag inte ska få veta 9.
Svaret är GIVETVIS (även om vissa lallande fjantar tror han är fiffig och har ställt en kuggfråga) att det finns ett oändligt antal tal jag kunde haft för att få 17 om jag ligger till ett tal som är okänt.
Det är bara lallande fjantar som tror att någon avsiktligt kastar bort mätdata (snarare dess derivat medelvärdet) så man inte kan återskapa det från anomalidata.
18 ovan ska vara 17, givetvis. Påpekar jag inte detta kommer väl babbel-Jonas göra ett stort nummer av att jag inte kan addera 8 och 9.
Att lägga till eller dra ifrån medelvärdet M är trivialt. Som du säger kan detta göras obehindrat, men bara så länge du vet exakt vet du vill hamna. Dvs vet vilket M du skall lägga till igen. Och som hade förklarats för dig redan från allra första början.
Det som är felaktigt är att du vill kallar det för en affin transformation, det faktum att du (i din version) har x1, x2 (mfl) både som variabel (i kolumnvektorn till höger) och dessutom inne i matrisen.
Om du har stulit ngt vet jag inte. Men inte har du kommit på ngt vare sig nytt eller speciellt användbart. I bästa fall ngt omständigt som ger rätt svar. Men ett svar som ingen efterfrågat (eftersom det är trivialt), och som har just den egenskapen du upplysts om redan för över ett år sedan (det är bara en fusklapp)
Om du inte kastar mätdatat har du det kvar, den delen har du också rätt i. Du kan tom kalla det ’obehindrat’. Varför du skulle dessutom vilja ha en (n+1)*(n+1)-matris för att ta fram data du redan har är svårt att förstå. Ngt sådant behov finns inte (det räcker fö med att spara M, och bara lägga till det för att återskapa mätvärden)
PS Bra att du klarar av av att lägga 8 till 9 eller dra ifrån igen.
Vi kan ta det från början. Det är nämligen inte det minsta svårt (för den som behärskar enkel matematik)
Mätdata X, och anomalidata Y är lika många, och den senare kan bestämmas ur den förra, men inte tvärtom. Eftersom det är linjära ekvationer finns det välutarbetade formalismer för sådant (grundkurs på universitetsnivå). Allmänt skrivs sådana samband:
Y= A*X + B (A- kvadratisk matris, B kolumnvektor av samma ordning som datats storlek)
Inverterbarheten avgörs helt av A:s egenskaper. B är en translation helt irrelevant för inverterbarheten, och dessutom noll för anomaliberäkningar. Sådana är alltså en linjär transformation, som dessutom är icke inverterbar.
Varför den är icke-inverterbar är också busenkelt att bevisa (för den som behärskar enkel linjär algebra)
OK, så vad handlar Björnes årslånga svammel om då? Jo, att om han får spara en fusklapp, då kan han från anomalidata återskapa mätdata. Det är helt sant, det är uppenbart och självklart och aldrig ifrågasatt. Men det är inte längre att invertera en algoritm (eller en matematisk operation)
Poängen (med att ngt är icke-inverterbart) är just att där finns oändligt många möjliga lösningar (indata) som ger precis samma svar, avbildningen är icke-entydig.
Av någon anledning (som möjligen ’förklaras’ av Björnes citat/länk i #136) vill Björne prata om att han visst kan invertera saker, bara han får ha kvar sin fusklapp. Och att det inte alls är en fusklapp, om man skriver in datat i sin algoritmen, som då inte längre är en algoritm för anaomaliberäkningar, utan bara gäller alldeles specifika (men icke-entydiga) uppsättningar av indata. Han tom demonstrerar att han inte kan avgöra om en viss uppsättning anomalier hör till hans sparade fusklapp eller inte. Dvs tom fusklappen är värdelös.
Hela poängen är förstås att det han kallar för ’invertera’ inte är någon invertering. Men det är förstås uppenbart, eller blir det senast då man skriver upp beräkningen korrekt: Y = A*X + B och studerar vad termerna har för egenskaper.
Här kommer ännu en gång Björnes uprsrungliga påstående rörande detta:
”JonasN: Ja du, matematik är inte din starkaste sida så mycket är säkert. Du är så okunnig att du inte ens inser hur okunnig du är. Och du förstår inte vad jag skriver trots att jag försöker förklara matematiken för dig på allra lägsta nivå. Men jag försöker igen:
Man kan skapa en uppsättning data (med tillhörande graf) utifrån en annan uppsättning data (med tillhörande graf) med hjälp av en algoritm av något slag. Den skapade uppsättningen data kan återskapas till den ursprungliga med hjälp av den inverterade algoritmen. Ingen av data uppsättningarna har någon annorlunda position i det matematiska universumet, det är helt arbiträrt vilket man betraktar som primärt eller deriverat”
se länk i #136. Kul är också hans efterföljande kommentar (#207 där) i vilken han hävdar:
”JonasN 205. Matte är faktiskt min starkaste sida”
Och det kanske tom stämmer …. gudbevars
🙂
Alla trådar där Björne har försökt briljera med sin ’intuitiva matematiska begåvning’ som ju ’är hans starkaste sida’ är rena guldgruvan. Kort efter ovanstående skrev Björne följande:
”Du är som sagt för okunnig inom matematik för att ens förstå vad du pratar om. Jag kan bara hänvisa till 206. Det vi pratar är om att transformera en uppsättning mätvärden till en annan, lika stor, uppsättning mätvärden via en algoritm. Den processen kan alltid inverteras utan att data går förlorade och det är där du gång på gång har visat hur okunnig du är om grundläggande matematiska processer. Att visa upp data som ett värde typ månadsmedeltemperatur eller som en avvikelse från genomsnittlig månadstemperatur,eller anomalier om du så vill, handlar enbart om att byta referenssystem via en algoritm. Och genom att invertera algoritmen kan du byta tillbaka referenssystem och inget data har gått förlorat och det går att exakt återskapa det du utgick ifrån, ditt första referenssystem. Och det var det diskussionen gällde”
Nåja, han har kommit lite liiiite längre sedan dess. Han inser numera att han inte kan gå åt båda hållen, att anomaliberäkningar inte är en entydig avbildning, och sålunda inte kan inverteras. Men om han säger att han aldrig någonsin hävdat ngt annat så ljuger han. Och han ljuger väldigt mycket när han blir trängd.
🙂
Jag borde inte ha klippt citatet (i #142) där, även fortsättningen är guld värd:
”Att skapa ett medelvärde av en uppsättning data är en enkel algoritm. Men man kan inte reversera den, Du kan inte återskapa den ursprungligen ingående data genom att invertera algoritmen. Det beror på att du ändrat mängden datamängden och den inverterad algoritmen får för många fria variabler och du får en oändlig lösningsmängd, dvs ingen lösning”
Som sagt, obetalbart! Och det kommer mer i samma kommentar:
”Har man däremot manipulerat en uppsättning data med en eller flera algoritmer (exempelvis subtraherat ett medelvärde, multiplicerat med en skalfaktor etc) utan att ändra dess mängd, dess antal, så kan du alltid återskapa den ursprungliga uppsättningen data genom att invertera algoritmen”
Om man är snäll går det att tolka ovanstående som att den ’intuitivt begåvade’ Björne med sin starkaste sida matematik bara var väldigt okunnig om enklaste matematiken. Att han då trodde att detta gick att göra, och att förklaringen ju var att tex en summa eller en medelvärdesberäkningar minskar antalat. Eller ngt senare att ett sort- eller basbyte (som är inverterbart) är matematiskt samma sak som att dra ifrån datats eget medelvärde, dvs en anomaliberäkning.
Men nu kan han inte apellera till sin ignorans längre. Och som sagt, under året där han försökt rädda ansiktet efter ovanstånde magplask har där kommit många fler av liknande och värre dignitet. Hans försökt att (mha Wikipedia) igen få det till att anomaliberäkningar är en translation (dvs beskrivs med en affin transformation) är det senaste.
Och vad som är tragiskt är att precis allt, och alla fel han har gjort, men inte borde, hade förklarats för honom både enkelt och korrekt och många ggr och ofta av flerast tom.
Sorry alla … jag blir så full i skratt. Varenda ett av Björnes efterföljande försk (se länk i #136) är så formidabelt i sina många dumheter och fel blandade med hans sedvanliga dryghet … att det det nästan är gulligt (om det hade varit en buskis-kommedi, vilket det tragiskt nog inte är)
I nästa kommentar skriver han att beräkningen av medelvärdet inte är en del av algoritmen för att bestämma anomalier. Utan att den ’algoritmen’ först kallas så efter att man från data bestämt medelvärdet! (*)
(*) Och det är ju den fusklapp han fortfarande håller fast vid idag så hårt idag, och kallar olika (ofta felaktiga) namn
BjörnT och Jonas N – nu får jag åter be er sluta med de interna diskussionerna. Jag har ju en gång sänt er varandras emailadresser.
Jag förstår inte varför Peter Stilbs hela tiden retar sig på detta. Är det inte Lena Krantz tråd?
B-J-B
2014/01/14 kl. 09:46
Dessa två har hållit internt på och käbblat om bl.a. matematiska spetsfundigheter, utan intresse för bloggen, i evigheter nu. Och fått milda varningar för det, och varandras email, med en uppmaning att fortsätta där.
På sin höjd kan det ha underhållningsvärde en kort tid, men sedan länge är det bara tröttsamt.