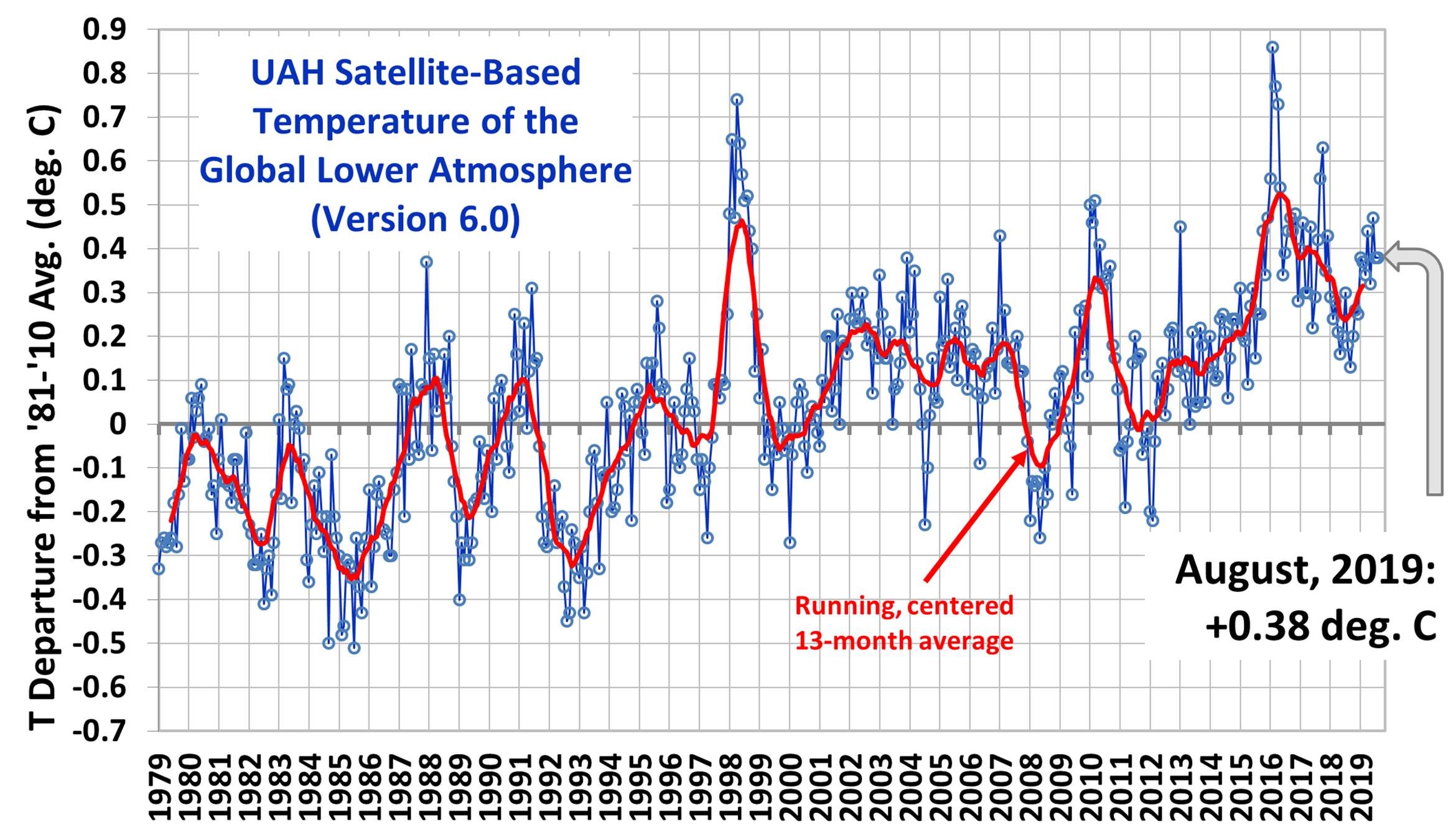
Vi fick just de senaste uppdateringarna från UAH och augusti slutade på +0.38 grader över medelvärdet mellan 1981-2010. Man försöker från dessa siffror utläsa trender och förutspå framtiden – 2000-talet var varmare än 80-talet, kommer platån under 2000-talet att bestå, finns det en cykel i el Niño mm? Frågan är dock om det överhuvudtaget finns någonting annat än en serie av slumpvärden som vi tittar på – eller rättare sagt om det vi ser dramatiskt skiljer sig från en slumpmässig förändring. Som människor har vi i ryggmärgen att vilja se mönster för att därmed kunna förutsäga framtiden. Denna förmåga får oss dock att se mönster även i slumpmässiga serie.
Om man tittar på UAH:s månadsvärden så ser den inte så slumpmässig ut. Om temperaturen var helt slumpmässig, inom ett visst intervall, så skulle vi visserligen ha en kurva som rörde sig upp och ner men det skulle inte vara så sannolikt att den första 200 värdena nästan uteslutande ligger under ett medel och de sista 200 nästan uteslutande över ett medel. Vi ser helt klart att ”någonting har hänt” under tiden och att vi har en ”trend” som måste betyda någonting. Att medelvärdet under 80-talet var -0,14 grader och medelvärdet på 10-talet är 0,24 grader måste ha en orsak och kan inte bara vara en effekt av slumpen…. eller? Detta är som jag hoppas kunna visa inte så säkert – en liknande utveckling skulle vi mycket väl kunna ha även om det bara var slumpen som styrde.
Tärningen är kastad
Om vi börjar med en helt vanlig tärning som istället för sidorna 1–6 har sidorna -3, -2, -1, 1, 2 och 3 så kan vi illustrera hur slumpen mycket väl kan skapa intressanta utvecklingar. Om vi slår en serie på 500 slag med tärningen så kommer vi får en slumpmässig serie med ett medelvärde troligtvis nära 0. Om vi ritar upp kurvan så får vi en hackig linje som visserligen kan ligga på plussidan i flera steg i rad med sannolikheten att den skulle ligga på plus 12 steg i rad (ett år) är mycket liten. Detta är vad vi vanligtvis förknippar med slumpmässiga serier.
I fallet med den globala medeltemperaturen, som med så många andra processer, så är det dock inte medeltemperaturen som är slumpmässig utan förändringen från föregående månad. Vi brukar säga att processen har ett minne och att den inte kan ta sig till vilket tillstånd som helst men den kan röra sig mot ett tillstånd och denna rörelse är slumpmässig. Om vi tar exemplet med tärningen så skulle de illustreras med att vi börjar på 0 och låter tärningen bestämma om vi skall flytta oss uppåt eller neråt på skalan och hur stor den förflyttningen skall vara. Det som nu sker är någonting som kanske inte är så väntat. Till en början så kanske kurvan rör sig upp och ner men sen händer det mycket ovanliga att vi slår två treor på raken (chans 1/36). Vi hoppar då upp nio steg och ligger kvar på en högre nivå tills slumpen ger oss en serie med flera negativa tal. Om vi råkar slå fyra -3:or på raken ( chans en på tusen) så har vi halkat ner 12 pinnar och det kommer nog ta oss ett tag att jobba oss upp ur den positionen.
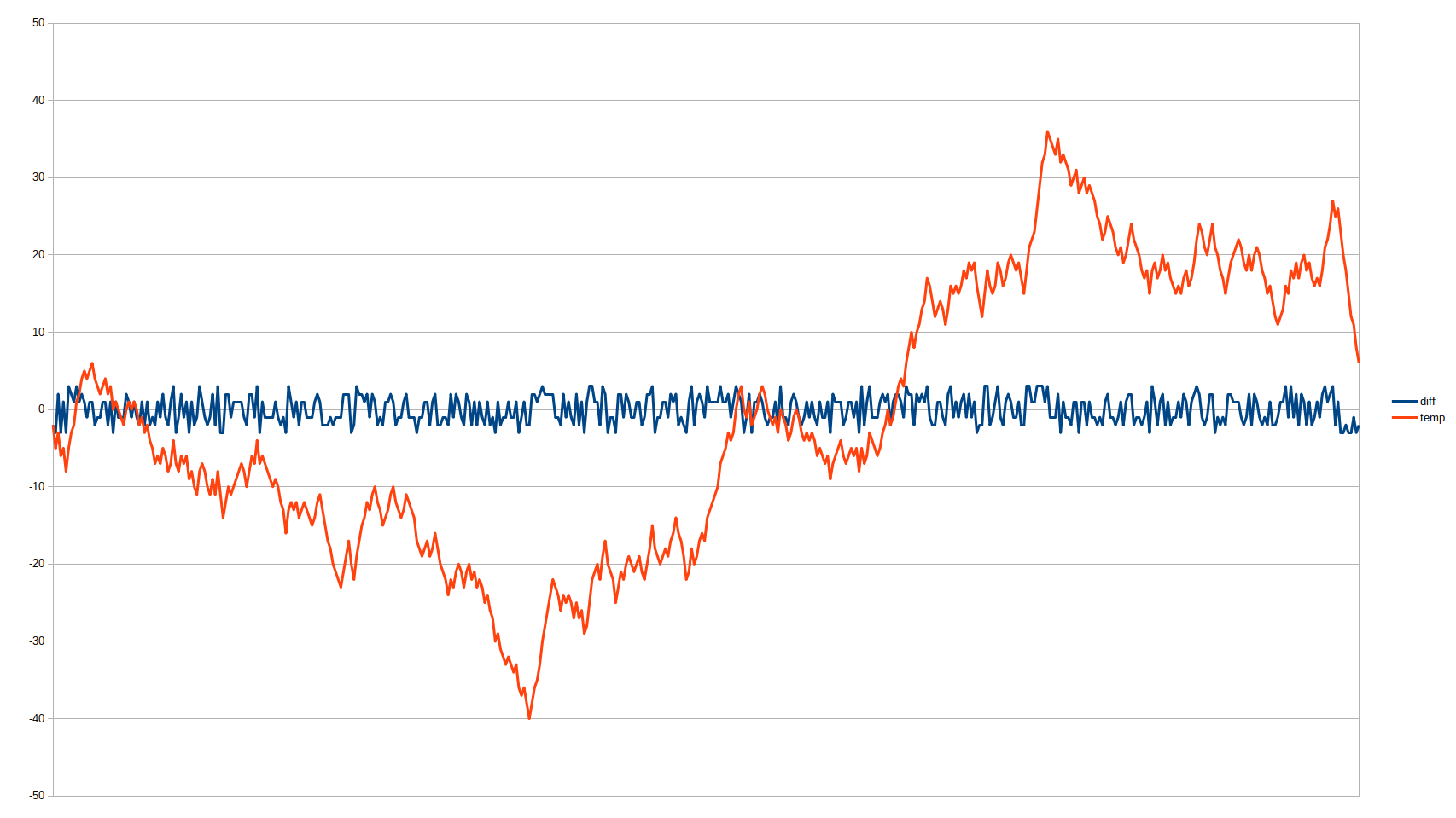
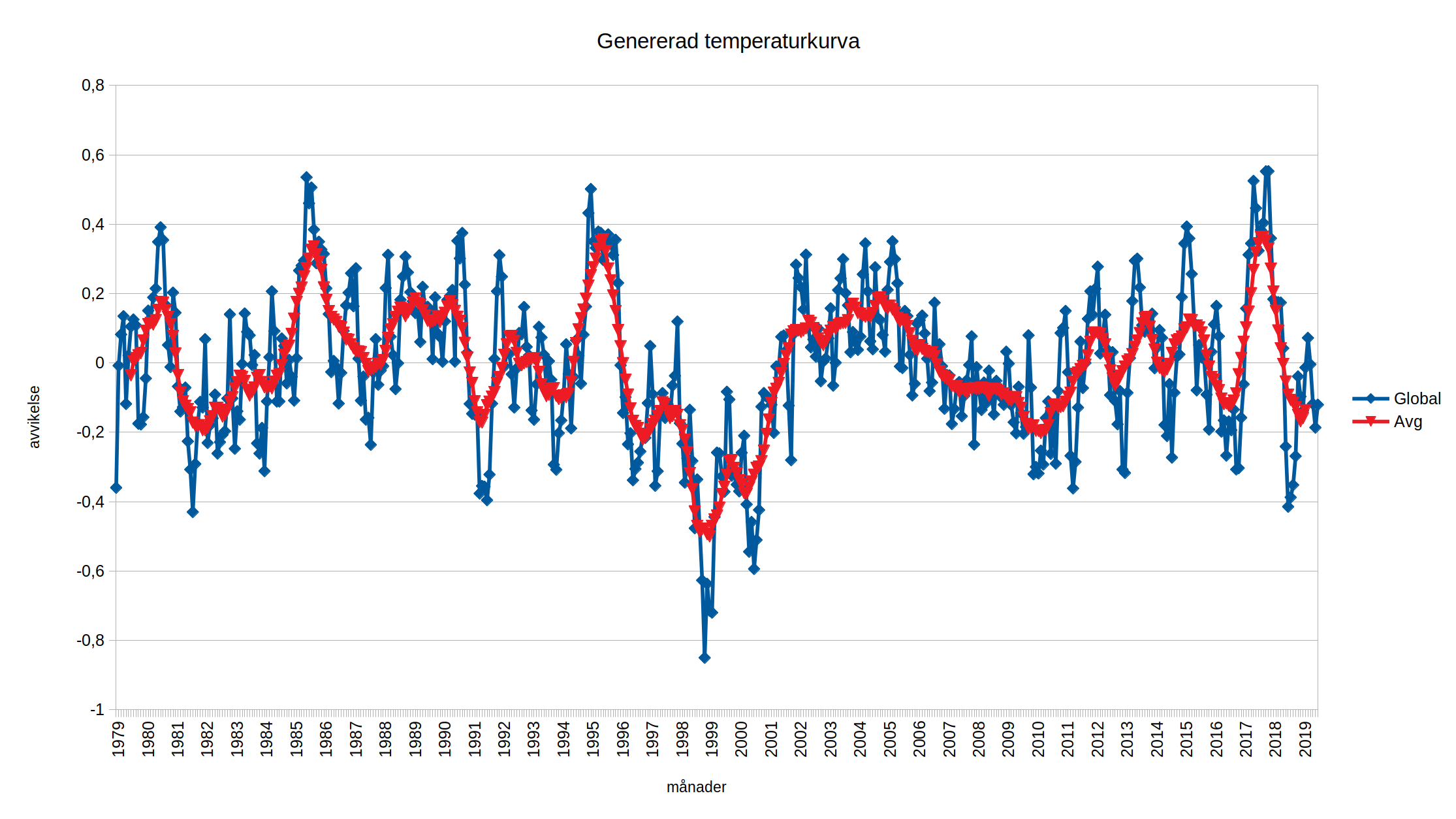
Här är en graf som visar hur vår serie skulle kunna se ut. Den blå kurvan är vad tärningen visar och den röda är den utveckling vi får. Om vi bara sett den röda kurvan så hade vi helt klart misstänkt att det fanns något bakomliggande som drev utvecklingen först nedåt, sedan uppåt för att sen
stabilisera sig (… och den sista störtdykningen är naturligtvis helt oförklarlig).
Temperaturförändringar
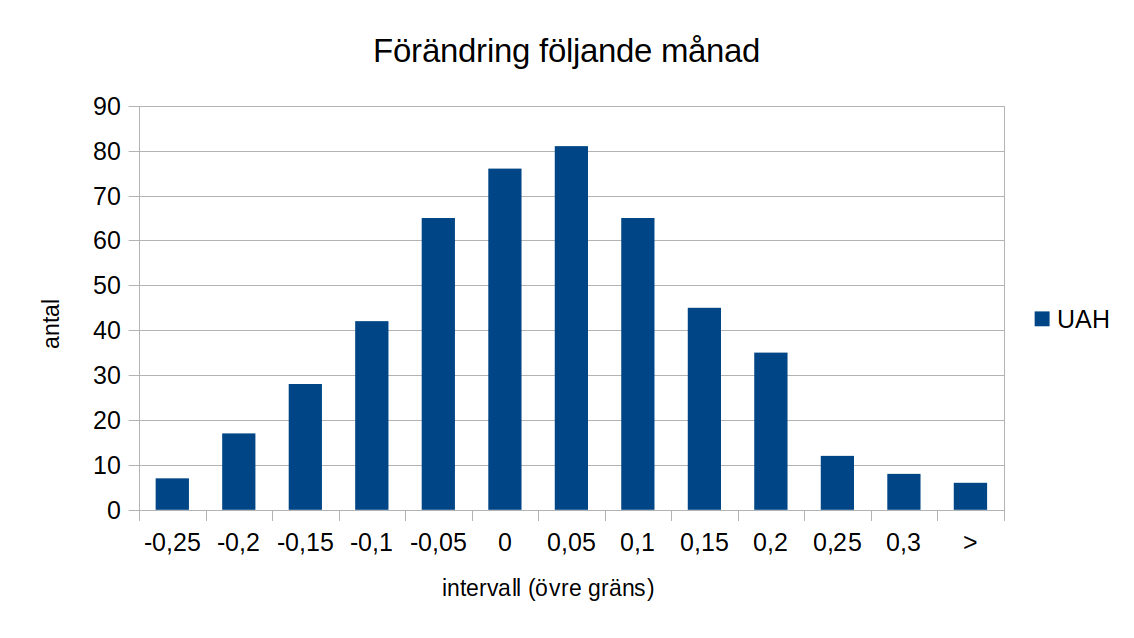
Kan den kurva som vi har i UAH-serien vara en effekt av en liknande slumpmässig förändring? I UAH-serien ligger förändringen månad för månad mellan -0.3 och +0.4 grader. Förändringen i detta intervallet är dock inte likformigt fördelat, det är betydligt vanligare med små förändringar än stora. Endast ca 10% är förändringar där temperaturen sjunker med mer än 0.15 grader och lika ovanligt är detta att temperaturen stiger med 0.15 grader, hela 30% av förändringarna ligger i intervallet +/-0.05 grader. Vi kan gruppera förändringarna i intervall om 0.05 grader och rita upp ett histogram för att bättre se hur fördelningen ser ut.
Distributionen är i det närmaste normalfördelad med ett medelvärde på 0 grader och standardavvikelse på 0.12 grader. Vi skulle kunna generera en kurva där vi slumpar förändringen givet den normalfördelningen men vi har ytterligare en faktor att ta hänsyn till.
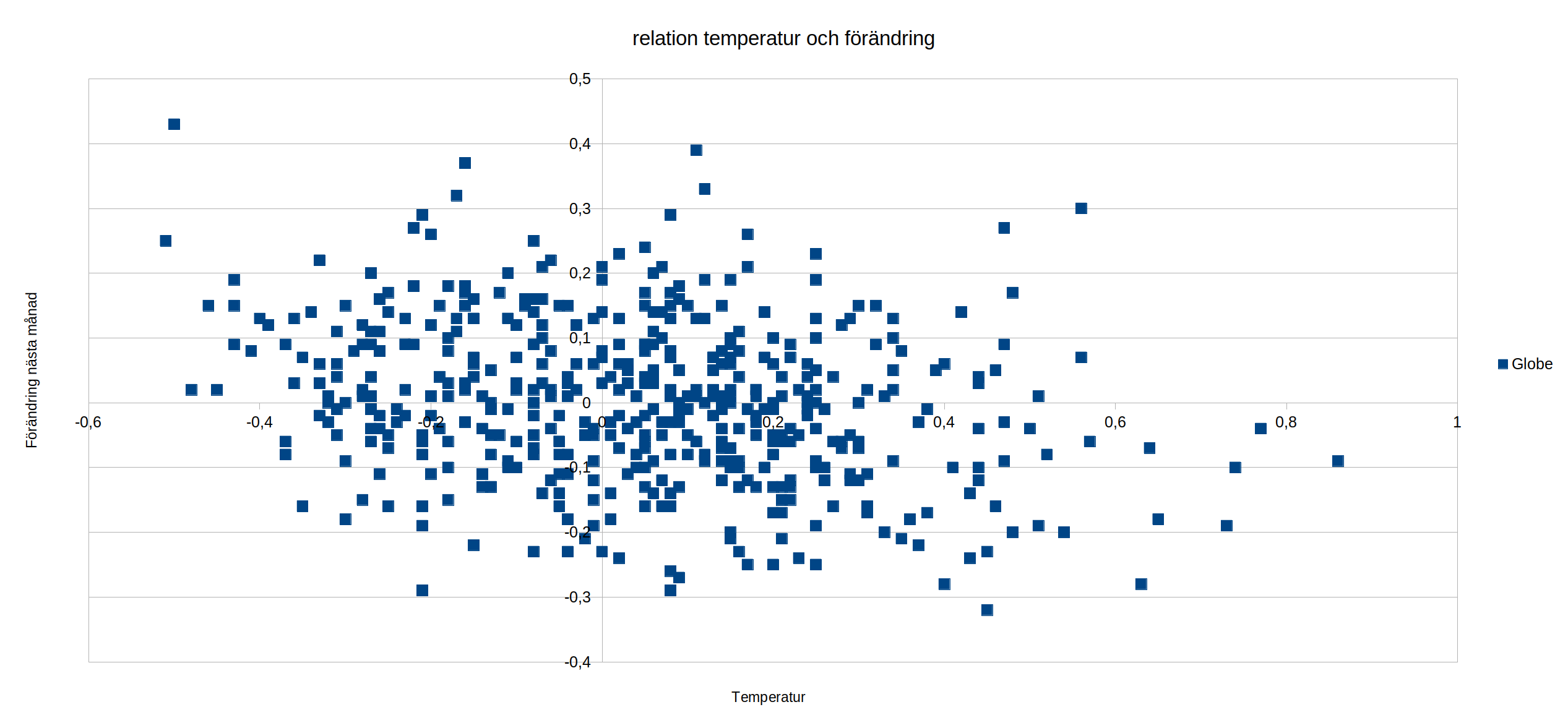
I fallet med tärningen så var varje förändring oberoende av vilken nivå vi låg på. Att den totala summan var över 20 hade inget inflytande på vad nästa tärningslag skulle resultera i. Riktigt så fungerar nog inte jorden, det är svårare att höja temperaturen på en redan varm värld än på en kall värld. Vi kan faktiskt se det i temperaturserien från UAH genom att jämföra temperaturen och förändring till nästa månad.
Som synes är hagelskuren inte helt symmetrisk, vid låga temperaturer är det vanligare att vi har positiva förändringar och vice versa vid höga temperaturer. En linjär approximation har en lutningpå -0.14 men korrelationen är som synes inte så stor.
Vi simulerar världen
Om vi vill modellera den dämpande effekten så kan vi låta normalfördelningen anta medelvärde som är omvänt proportionerligt mot temperaturen. Vi tar faktorn -0.14 så kan vi generera en temperaturserie som statistiskt sett överensstämmer med UAH. Nedan ser vi resultatet av en sådan serie.
Hade vi inte vetat att kurvan var helt slumpmässig så skulle vi börja fundera över vad som gjorde att temperaturen föll under 90-talet (om vi bortser från ”El Niño” 1995), den kraftiga uppgången i början på 2000-talet och den ovanliga stabiliteten på 10-talet.
Gud spelar inte tärning*
Är det då bara slumpen som styr vår temperaturutveckling? Troligtvis inte – men det är med de data som vi har för den globala medeltemperaturen månad för månad under de senaste 40 åren mycket svårt att skilja utvecklingen från en utveckling som är slumpmässig.
Vi vet naturligtvis att de stora temperaturförändringarna som vi ser i UAH 1988 1998 och 2016 är s.k. el Niño-fenomen men vad styr dessa? Det är notoriskt svårt att förutse el Niño så vi kanske måste betrakta dessa som slumpmässiga. Visst vet vi att det är fysikens lagar som styr såväl jordens energibalans som havens cirkulation och att ingenting händer av en slump, men om vi bara betraktar slutresultatet så behövs inte mycket mer än slumpen för att ge en förklaring.
Johan Montelius
* För de klassiska fysikerna var kvantfysikens synsätt, där en fysikalisk storhet som rörelsemängd eller spinn inte antar ett värde innan en mätning utförs, främmande och Albert Einstein är känd för att ha ifrågasatt det med orden ”Gud spelar inte tärning [med universum]”. https://sv.wikipedia.org/wiki/Einstein%E2%80%93Podolsky%E2%80%93Rosen-paradoxen

Lektor inom datakommunikation, KTH.
I <3 CO2 – Koldioxid är kanske inte världens viktigaste gas men den kommer som bra tvåa efter syre.








”…1988 och 2016…” ska väl vara 1998 och 2016? Kraftig El Nino 1982 också … I runda slängar halvannan solfläckscykel… Slumpen?? Tror inte det… Kollade just SMHI MAX MIN fredag 6/9/2019
20:00 till 08:00 lörd 7/9/2019 Nederbörd Svenska Högarna 989,0 mm … ingen asterisk om ” ligger
utanför tidigare kända extremvärden” Någon hemma på SMHI i veckosluten??
En amatörfundering. Det finns ju många olika faktorer som påverkar klimatet. Några med känd cyklicitet.
Cyklerna är olika långa och troligen inte styrda av varandra. Då borde det ju var rimligt att anta att de slumpmässigt förstärker eller förminskar varandras temperaturpåverkan. Eller?
#1 Staffan Lindström
rätt 1998 skall det vara
”Slumpen?? Tror inte det… ”
Hur långa serier skulle vi behöva för att kunna avfärda slumpen?
Tack Johan M,
det är bra för oss skeptiker att veta att temperaturutvecklingen de 40 år som vi tror oss kunna förstå skulle kunna vara heltslumpmässig
Men det är knappast något vi kan säga till en klimathotstroende — de skulle nog skratta rått
#2 Evert Andersson
Visst finns det cykler som styr klimatet men dessa är nog cykler på tiotals, hundratals eller tusentals år. De samverkar naturligtvis men för att säkerställa hur stor inverkan de har behöver vi temperaturserier som är bra mycket längre än 50 år. Kortare cykler finns säkert det också men dessa tycks till mångt och mycket drunkna i andra mer eller mindre slumpmässiga förändringar.
#4 Sten Kaijser
”— de skulle nog skratta rått”
Du har nog helt rätt och det har nog med vår inneboende vilja att förstå och kunna förutsäga händelseförlopp. Att någonting skulle vara slumpmässigt har vi och (som Ingemar gav en fotnot till) även Einstein svårt att ta till oss.
Förr i tiden, när meteorologiskrået genomgående var sansat, definierade man ”klimat” som medelvärde av väder över 30 år – underförstått att allt annat var slump. Så ej längre.
Nu är det klimatförändringar dag och natt i vissas hjärnor
En mycket bra och tankeväckande inlägg, det håller jag med om.
De tankar jag får är flera, de har en gemensam faktor:
det blir allt mer uppenbart för mig hur lite vi människor vet och förstår hur land, hav och atmosfär samverkar, och ffa vad resultatet blir på kort och lång sikt. Lägger man till den påverkan som finns i vårt solsystem, främst solen men även vår omloppsbana och kosmisk strålning, och inte minst klimatets långa cykler, blir det futtigt och närmast larvigt att ens tänka tanken att mänsklig aktivitet öht. påverkar nämnvärt.
Hur kan man avgöra om en slumpmässig serie skiljer sig från en serie med ett orsakssamband eller åtminstone någon form av korrelation? Jag antar att man under vissa förutsättningar kan använda sig av tex Monte Carlo simuleringar eller permutationstest för att få viss vägledning.
#9 mattias
”Hur kan man avgöra om en slumpmässig serie skiljer sig från en serie med ett orsakssamband eller åtminstone någon form av korrelation? ”
En mycket bra fråga som jag med varm hand bollar vidare till Sten Kaijser. Skulle jag ge mig i kast med en förklaring så skulle det nog skapa mer oreda än klarhet:-)
Intressant att det skulle kunna vara slumpen som genererat en sådan mätserie, men som gammal lantbrukare kan jag konstatera att uppvärmningen är påtaglig. Tidiga skördar och växter som fläder och hassel sprider sig numera som ogräs runt uthusen. Att det skulle ha att göra med co2-utsläpp är däremot ytterst osannolikt enligt min mening.
3 Johan M
Jag tenderar att alltmer tro att universum är totalprogrammerat… möjligen med vissa ”ad libitum”-partier… Läste upp mig lite på ”El Nino” på wiki. Intressant att inga El Ninos förekom 1926-41 Värstingvärmeböljornas tid, särskilt i Nordamerika?! … Så…vet ej….
7 Peter Stilbs

Du skrev faktiskt ungefär det som jag först tänkte svara Johan M Post nr 3…Slumpen vs/eller Gud?
Använder man sig av mätningar endast från stationer som inte påverkats av HUI och maritima förhållanden får man ju en kurva där man lätt urskiljer 60-65-årscykeln
https://notrickszone.com/2018/05/03/its-here-a-1900-2010-instrumental-global-temperature-record-that-closely-aligns-with-paleo-proxy-data/
Willie Soon har gjort i stort sett på samma sätt och fått en mycket lik kurva
Här finns mer om naturliga cykler: https://klimarealisme.dk/2019/05/04/en-raekke-af-forskere-spaar-en-periode-med-global-afkoeling-i-de-kommende-aar-hvorfor-goer-de-det/
Nån så kallad slump kan inte finnas i universum. Allt har sin orsak och verkan
Nej, allt är inte slump! Även om vi har ett delvis kaotiskt klimatsystem, så måste vi fråga oss vad det är som driver detta kaotiska system. Givet är att det är solen, men denna sol är inte ”konstant”, den varierar quasiperiodiskt över tid, med vilket menas att den varierar inte exakt periodiskt i sitt beteende. Vi har 11-årscykler, grand solar maximum/minimum och dessutom planeternas rörelser vilka påverkar vårt solsystems masscentrum etc. Detta quasiperiodiska beteende hos solen tillsammans med planeternas rörelser, medför ett variabelt energiflöde mot jorden. Detta i sin tur medför förändringar i de oundvikliga quasiperiodiska system som exempelvis El Nino med flera, är. Jorden är inte en slät och homogen sfär på grund av berg och djupa hav med dess oregelbundna strandformationer. På grund av vissa osymmetrier i vårt solsystem tillsammans med vår jords, uppstår quasiperiodisitet. Men det är då också uppenbart att jordens olika vågsystem som exempelvis El Nino etc, interfererar och medför ett i betraktarens öga, ett kaotiskt system.
Jag undrar om inte författaren dragit fel slutsats vid sitt scatterdiagram, som lutar -0.14, när han säger att ”korrelationen inte är så stor”. Jag skulle gissa att den kan vara rätt stor, kanske 70%. Den pessimistiska visuella bedömningen har säkert påverkats av att intervallen på x- och y-axlarna är olika dimensionerade.
Det kan väl ändå verka som det är mer sannolikt än inte, att vi får El niño precis efter solminimum.
By knowing or estimating where in the solar cycle we are we can get an estimate of the chances of a particular outcome even years ahead.
https://curryja.files.wordpress.com/2019/09/figure-2.png
It is clear that even in a crude form solar activity is useful for ENSO prediction and no doubt the method can be improved enormously
https://judithcurry.com/2019/09/01/enso-predictions-based-on-solar-activity/
Eftersom vi numera har La niña liknande tillstånd har vi troligen några månader kvar på solminima innan det vänder upp igen.
#17 Anders Persson
Du har en poäng. Sitter i bilen just nu men skall kolla siffrorna asap.
2015 höll jag en veckokurs i statistik i Bologna. På torsdagen ägnade jag en hel föreläsning åt det som kallas ”regression to the mean” effect
https://hepex.irstea.fr/wp-content/uploads/2013/12/Lecture_19.pdf vilken kan generera höga men totalt ointressanta korrelationer.
Solskenstiden har ökat stadigt de senaste åren vilket visas på SMHI:s bild som finns här.
https://www.smhi.se/polopoly_fs/1.143989.1548428766!/image/allsack_1983-lastyear.jpg_gen/derivatives/Original_1256px/image/allsack_1983-lastyear.jpg
#17 Anders Persson
Jag får en korrelation mellan temperatur och förändring på -0.26.
#15 Kent B
”Nån så kallad slump kan inte finnas i universum. Allt har sin orsak och verkan”
Jag tror en hel del kvantfysiker skulle ha lite att invänd där.
OT
Jordsystemforskare (sic) Rockström Skriver följande i en artikel i DI som ligger på nätet:
”Ökningen av medeltemperaturen på jorden har, enligt de senaste publicerade studierna, inte överskridit två grader de senaste tre miljoner åren, trots stora naturliga svängningar mellan istid och varmare mellanistider.
Vi har nu genom utsläpp av växthusgaser höjt temperaturen med 1,1 grader – troligen den varmaste medeltemperaturen sedan den förra istiden, för 12 000 år sedan.”
De studier jag sett visar på betydligt större temperaturvariationer än två grader de senaste tre miljoner åren. Vilka ”senaste publicerade studierna” är det Rockström utgår ifrån?
En bra beskrivning av hur autokorrelation påverkar slumpprocesser. Praktiskt taget alla klimatiska fenomen är mer eller mindre autokorrelerade. Fenomenet uppmärksammades först av Hurst, en engelsk hydrolog som studerade variationerna i Nilens vattenföring, där man har årtusendelånga dataserier. Det kallas därför för ”the Hurst phenomenon” eller ”fractional gaussian noise” eller ”fractional brownian motion”.
Fenomenet är som sagt mycket vanligt, för att inte säga universellt, i klimatsammanhang men mer eller mindre okänt för de flesta, tydligen inklusive många klimatforskare. Det luriga med det är att en autokorrelerad slumpprocess inte ser slumpmässig ut. Vi luras som så ofta av vårt nervsystem som är extremt bra på att hitta mönster, faktiskt så bra att vi ständigt ser mönster där det inte finns något.
Att inte korrigera för autokorrelation är ett av de vanligaste statistiska felen inom klimatvetenskapen, men tyvärr långt ifrån det enda.
Apropå klimatcykler så har det visat sig väldigt svårt att hitta några säkra cykler utöver årscykeln och milankovichcyklerna. Solfläckscykeln är förvisso reell, om också av varierande längd, men annars är det glest. De flesta andra ”cykliska” klimatfenomenen (NAO, PDO, ENSO, IOD o s v) är så varierande i ”cykellängd” och amplitud att de lika gärna kan vara exempel på ”the Hurst Phenomenon”. Inom paleontologin, som ju studerar mycket långa tidsintervall har det också visat sig mycket svårt att hitta några tillförlitliga cykler utöver dygn, år och de olika Milankovichcyklerna. ”Kalibrering” av geologiska intervall bygger i princip helt på radioaktivt sönderfall och Milankovichcykler, och någon enstaka gång årsrytmiter.
För övrigt så har det visat sig att djupast så är t o m planeternas banor och de astronomiska cyklerna i solsystemet kaotiska, men på så lång sikt att bara geologer påverkas, och ofta inte ens de.
För den som vill sätta sig in i fenomenet litet djupare rekommenderas denna artikel:
https://www.tandfonline.com/doi/pdf/10.1080/02626660209492961
Den är skriven av Demetri Koutsoyiannis, en grekisk hydrolog som är en ledande specialist inom området och är någorlunda lättbegriplig.
#24
”De studier jag sett visar på betydligt större temperaturvariationer än två grader de senaste tre miljoner åren. Vilka ”senaste publicerade studierna” är det Rockström utgår ifrån?”
Det går nog att skaka fram. Det har skett en omfattande ”justering” av paleoklimatiska siffror de senaste 10-20 åren, och data som är svåra att trolla bort som t ex förändringar av trädgränser och snögränser ignoreras alltsomoftast. Det hela har blivit litet absurt när man på fullt allvar hävdar att det t ex skulle vara mindre än 5 graders skillnad globalt mellan glacialer och interglacialer. Fem grader mellan flodhästar och inlandsis i England alltså, eller fem grader mellan apor och tundra i Bayern? Det känns som om skillnaden nog är något större i nutiden.
Och det holocena optimat skall ju gudbevars inte ha varit varmare än nu. Då fanns det kärrsköldpaddor och sjönöt i Roxen, men jag har inte sett till någondera än. Och inte har spannmålsodlingen på Grönland tagit fart heller.
#11
”Tidiga skördar och växter som fläder och hassel sprider sig numera som ogräs runt uthusen. Att det skulle ha att göra med co2-utsläpp är däremot ytterst osannolikt enligt min mening.”
Du glömmer en tredje extremt viktig faktor: ökad näringstillförsel, framför allt kväve, både via luften och genom avrinning från odlingsmarker. Att detta är viktigt framgår av att arter som vill ha näringsfattig mark försvinner i snabb takt. När såg du en ormrot eller kattfot, för att inte tala om en ängsgentiana eller mosippa senast? Och när jag var ung var ängsnattviol (som vill ha näringsfattig mark) vanlig och den grönvita nattviolen (som trivs på näringsrik mark) sällsynt. Nu är det tvärtom.
Fläder är f ö ett mycket dåligt exempel eftersom den är inkommen i sen tid och fortfarande sprids successivt av fåglar.
# 23 Johan M
Jag har också läst om det men har en känsla att de tar till med slumpen när de inte kan förklara vissa saker. Jag menar att allt måste vara lagbundet på något sätt och allt måste ha en orsak som ger en verkan
tty #25,
Peter Stilbs skrev om Hurstfenomenet och Nilen bl.a. här:
https://www.klimatupplysningen.se/2016/03/21/monster-kaos/
#27:
Jag har bott här i Örebrotrakten i runt 60 år och före sekelskiftet hände det flera gånger att vår enda fläderbuske frös ner helt under vintern. Nu har detta inte inträffat på länge och minst ett tiotal nya buskar har dykt upp i omgivningen, så min känsla är att fläderns nordgräns har flyttat norrut. När betesdjuren försvann har förstås näringen anrikats i markerna och smultron och kattfot har ersatts med hundkäx och brännässlor och annat som kan ta tillvara växtnäringen, inkl co2. Inte lika trevligt men naturens sätt att anpassa sig. Att skördeperioden har tidigarelagts med ett par veckor kan inte bortförklaras. Tidigare sorter, högre maskinkapacitet både vår och höst har så klart bidragit en del.
Intressant i sammanhanget ”the Hurst phenomenon”. Speciellt sidan 37 i nedanstående länk. Men först en definition (sid 19): Hurst phenomenon (“phenomenon” may imply that Mother Nature’s reality is something extraordinary or exceptional).
http://www.itia.ntua.gr/en/getfile/849/3/documents/2008EGU_HurstClimatePrSm.pdf
# 22 Johan M: Kan du göra mig en tjänst, ”för gammal vänskaps skull”? Om det är enkelt för dig beräkningstekniskt, skulle du kunna göra om korrelationsberäkningen under antagande av minne=0, dvs helt slumpmässiga förändringar. Min intuition, som jag inte litar på och vill kolla, säger mig att då blir lutningen cirka -1.0 opch korrelationen omkring 0.7.
#32 Anders Persson
Visst fixar jag, men korrelation mellan vad? Det jag gör är att ta korrelationen mellan temperaturen och förändringen till nästa månad och får -0,26. Det är 488 månader i serien angivna med två decimaler; i diagrammet är de mer centrala punkterna multipler medan uteliggarna är enskilda. Kan det vara det som gör att man ser en större korrelation än vad det är?
När du säger minne=0 så förstår jag inte. Om jag tar korrelationen för två på varandra följande månader så får jag korrelation 0.85 (linjär lutning 0.86) vilket är rätt intuitivt; hur är vädret i morgon – som idag med stor säkerhet. Men det är ju inte det du menar, vilka värden är det vi skall kolla på.
…och, tittar gärna närmare på siffrorna – det var ett bra tag sen jag gick kursen i statistik och det är inget jag gör dagligdags så jag lär mig.
#27 tty
OT. Som vanligt från din sida ytterst initierad och kunnig kommentar. Du nämner några kärlväxter som klarar näringsfattiga vs gynnas av näringsrika markförhållanden. Från min synvinkel och erfarenhet bör nog även skogsbete, fäbobruk samt slåtter vägas in i förklaringar till förekomst av t ex ormrot, kattfot och ”vanlig” nattviol. Naturen och arterna är hur som helst fascinerande!
# 32 Anders Persson
”minne=0”. Visst menar du slumpning med återläggning?
#30 Bert Nilsson
”..kan inte bortförklaras. ”
Att det blivit varmare sedan 60-70-talet är väl helt klart. Frågan är om det betyder någonting – klimatförändringar är det mest naturliga som finns och det mest osannolika vore att klimatet inte förändrades. Huruvida det sen beror på förändringar i solaktivitet, variationer i oceanernas rörelser eller … människans bidrag av koldioxid, kan diskuteras.
#20 Anders Persson
”2015 höll jag en veckokurs i statistik i Bologna.”
Jag hittade fler föreläsningar under samma URL – en guldgruva. Ser fram emot dessa i form av inlägg på Klimatupplysningen
”Jag har bott här i Örebrotrakten i runt 60 år och före sekelskiftet hände det flera gånger att vår enda fläderbuske frös ner helt under vintern. ”
Måste vara stor skillnad på kort sträcka, för här i centrala Östergötland har jag aldrig upplevt att någon av fläderbuskarna på tomten har frusit, inte ens under de hårda vintrarna på 70-talet.
#33 Johan M: Jag förstod att den blå kurvan var tärningskasten i original, den röda med en slags inbyggd ”tröghet” eller minne. För den röda kurvan blev korrelationen mellan temperatur och förändring liten. Men hur stor är den för den blå kurvan?
#39 Anders Persson
I den andra grafen där vi kastar en tärning med -3/+3 med jämn fördelning så är blå kurva tärningsutfall och den röda den ackumulerande summan.
I den femte grafen så är den blå kurvan den ackumulerande summan då vi slumpar från en normalfördelad sannolikhet som även har en bias för dämpning. Den röda kurvan är helt enkelt ett flytande medelvärde för 13 ”månader” precis som vi har i den första grafen för UAH serien.
Jag gjorde först en graf där man bara slumpade ur normalfördelningen men den visade alltid betydligt större variation än UAH. UAH har ju ett spann på -0.5 – +0.8 men det man fick slog lätt på -1 – +1 och ofta mera. Det var då jag la in dämpningen genom att låta normalfördelningens medelvärde vara omvänt proportionellt med temperaturen. Säkert en grov generalisering som inte är exakt det vi letar efter men i alla fall något som för in en dämpande effekt.