Murry Salbys ekvation säger att koldioxidens ökningshastighet i atmosfären bara beror på temperaturen och följaktligen är oberoende av antropogena emissioner. Ekvationen motsäger alltså den etablerade teorin för kolcykeln enligt vilken ökningen i koldioxidhalten i atmosfären helt beror på antropogena emissioner. Det sensationella med Murry Salbys ekvation är att den anmärkningsvärt bra överensstämmer med hur koldioxidhalten har ökat enligt mätningarna.
Som jag redan från börjat påpekat så kan det vara av en tillfällighet som ekvationen överensstämmer med observationerna, att den egentligen stämmer med den etablerade teorin. Men någon trovärdig sådan förklaring finns ännu inte.
Det är förmodligen också så att den etablerade kolcykelteorin är väl förankrad hos kolcykelforskarna. Även om det kommer fram resultat som strider mot en etablerad teori så är det vanligen en lång process innan man överger centrala delar i en sådan, speciellt i det fallet som vi har här att kolcykelteorin är mycket komplicerad.
Murry Salbys resultat har ännu inte publicerats utförligt i en vetenskaplig artikel så jag bygger på mina egna resultat av att jämföra hans ekvation med observerade data. Här ger jag bara en översikt men en detaljerad diskussion finns i en fördjupningsrapport (Björnbom, 2013).
Murry Salbys ekvation är:
Parametervärdena är de jag bestämt genom parameteranpassning enligt tidigare blogginlägg även diskuterad här.
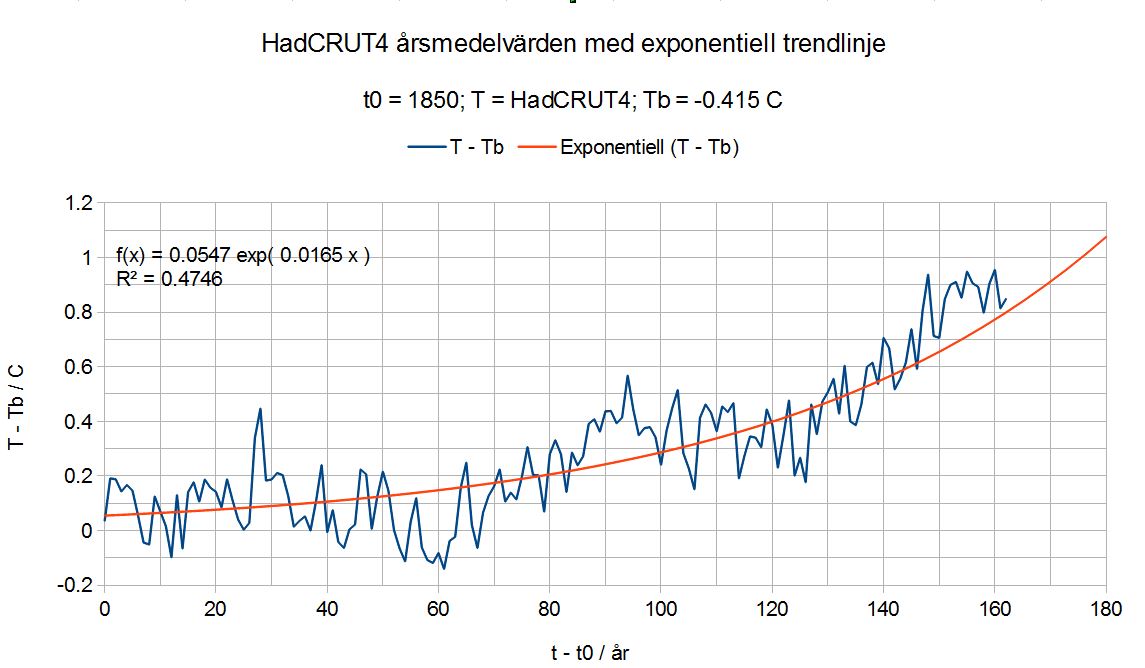
Diagrammet ovan visar temperaturavvikelser enligt HadCRUT4 med exponentiell trendlinje. För att man skall kunna bestämma en sådan trendlinje måste man specificera det värde på temperaturavvikelsen där temperaturen planar ut mot en horisontell linje. Detta värde angav jag till motsvarande värde som jag bestämt för Murry Salbys ekvation, Tb = -0.415 C. För att få mer hanterbara siffror har jag satt år 1850 till år noll.
Man skulle kunna förklara temperaturtrendens ungefärligt exponentiella form med att den totala externa forcingen från växthusgaser är nära exponentiell, se diagram enligt Schwartz i ett blogginlägg av Lennart Bengtsson. Lägg märke till temperaturkurvan avviker från den exponentiella trendlinjen de senaste 15 – 20 åren, den ligger klart över denna.

Diagrammet ovan visar hur Murry Salbys ekvation beskriver koldioxidhalten från tidigare blogginlägg. Ekvationen har anpassats till observerade data genom linjär regression vilket gett ovan nämnda parametervärden.
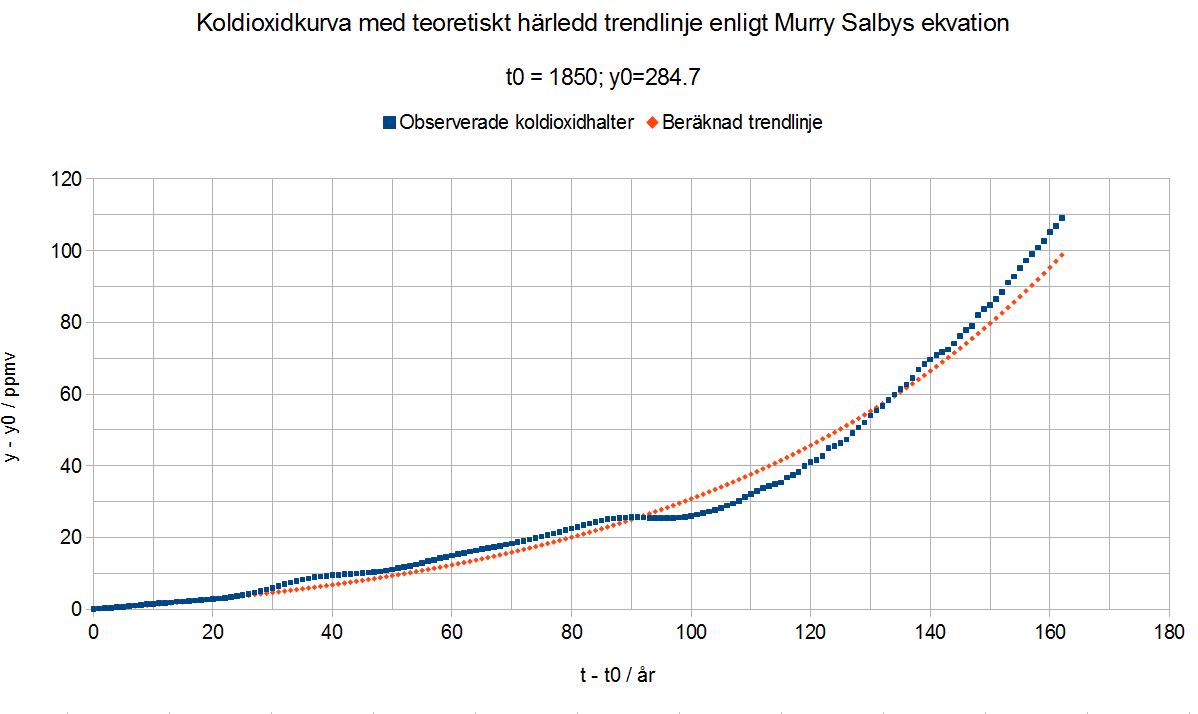
För diagrammet ovan har jag utgått från ekvationen för den exponentiella trendlinjen för temperaturen i figur 1. Jag har sedan med hjälp av Murry Salbys ekvation härlett en teoretisk trendlinje för koldioxidhalten. Diagrammet visar observerad kolhaltskurva jämförd med den teoretiskt härledda trendlinjen vars parametervärden är kända från de tidigare beräkningarna (så denna trendlinje har alltså inte anpassats med minstakvadratmetoden utan beräknats direkt). Denna trendlinje planar ut vid ett värde på kolhalten av yb = 277.4 ppmv som alltså motsvarar temperaturavvikelsen Tb = -0.415 C.
Denna teoretiskt härledda trendekvation visar sig vara densamma som dataprofessorn Lars Karlsson på UI har anpassat till observerade kolhaltsdata genom att variera tre anpassningsbara parametrar. Det är alltså ingen tillfällighet att Lars Karlsson med denna ekvation har fått en hygglig anpassning till observerade data, utan detta förutsägs av teorin.
En intressant sak är att den teoretiskt härledda trendlinjen stämmer sämre med observationerna de sista tjugo åren än den beräknade koldioxidkurvan enligt figur 2. Den senare kurvan stämmer otroligt bra med observerade data för denna tidsperiod och ger korrekt ökningshastighet.
Orsaken till denna skillnad mellan de två beräknade koldioxidkurvorna är att den exponentiella trendlinjen för temperaturen enligt figur 1 inte stämmer så bra med observationerna de sista tjugo åren. Man måste ha klart för sig att temperaturen inte bara påverkas av koldioxidkurvan utan även av till exempel metankurvan som har en annan form samt av naturliga variationer såsom uppvärmningspausen.
Trendlinjen för temperaturen ligger för lågt i detta fall vilket ger för låg ökningshastighet enligt Murry Salbys ekvation, något som inte sker när Murry Salbys ekvation tillämpas direkt på temperaturdata i stället för på den exponentiella trendlinjen. Om det finns ett systematiskt fel i temperaturdata ger alltså Murry Salbys ekvation en koldioxidkurva som inte stämmer med observationerna.
Jämförelse av de beräknade koldioxidkurvorna i figur 2 och figur 3 har diskuterats i fördjupningsrapporten. Den tyder på att det att Murry Salbys ekvation stämmer med observationerna inte beror på att temperaturkurvan har nära nog en exponentiell trend, vilket har föreslagits som förklaring.
Uppdatering 2013-07-26
Mina argument har tydligen inte gått fram till Lars Karlsson på UI så jag utökar mitt resonemang som följer.
Lars Karlsson har visat att en exponentiell koldioxidkurva ger en approximativt exponentiell temperaturkurva som ger tillbaka en approximativt exponentiell koldioxidkurva med Murry Salbys ekvation. Detta gäller när koldioxidhalten ligger mellan 300 och 400 ppmv. Han drar slutsatsen att det att Murry Salbys ekvation stämmer med observationer beror på en tillfällighet.
Men detta är en förhastad slutsats. I samma intervall för koldioxidhalten, 300 till 400 ppmv, ger nämligen även Murry Salbys ekvation kombinerad med temperaturekvationen enligt den enkla energibalansmodellen (EBM) en exponentiell koldioxidkurva tillsammans med en exponentiell temperaturkurva (detta beror på att vi får ett approximativt linjärt diffekvationssystem). Temperaturkurvan måste då naturligtvis ge koldioxidkurvan enligt diffekvationssystemets lösning när man tillämpar Murry Salbys ekvation på den. Jag har redan tidigare påvisat detta med en klimatsimulering:
https://www.klimatupplysningen.se/wp-content/uploads/2013/06/Beräkning-koldioxid-temperatur.pdf
Alltså, även om det endast var koldioxid som var extern forcing förutom slumpmässiga naturliga variationer så skulle en exponentiell koldioxidkurva inte motsäga Murry Salbys ekvation. Den exponentiella koldioxidkurvan skulle i så fall kunna ha två likvärdiga förklaringar, den ena att den blivit exponentiell genom människans utsläpp, den andra genom att koldioxidhalten följer Murry Salbys ekvation.
Men Lars Karlsson har i sitt resonemang och sina numeriska experiment gjort en fundamental miss som strider mot etablerad klimatvetenskap. Han förutsätter att enda externa forcing kommer från koldioxiden. Men enligt den etablerade klimatvetenskapen så påverkas temperaturen också av forcings från växthusgaser såsom metan och klorfluorkarboner och diverse aerosoler med mera. Hans analys håller därför inte.
Detta medför också att temperaturkurvan i realiteten avviker från exponentiell form, men trots detta visar sig Murry Salbys ekvation beskriva koldioxidkurvan mycket bra under de sista tjugo åren då vi har de bästa observationerna av både koldioxid och temperatur. Temperaturen har som bekant planat ut under uppvärmningspausen vilket enligt Murry Salbys ekvation innebär att koldioxidhalten skall öka med en konstant hastighet av knappt 2 ppmv/år. Denna överensstämmelse mellan Murry Salbys ekvation och observationer är mycket tydlig i figur 2 och stämmer väl med Wanninkhof med flera (2013) som i slutet på avsnitt 2.1 skriver att koldioxidhalten ökat med 1,8 ppmv/år från 1990 till 2009.
Lars Karlsson får göra om och göra rätt. Den väg han försöker sig på att bortförklara Murry Salbys ekvation är helt enkelt vetenskapligt igenbommad
Uppdatering 2013-07-29: Avrundning av diskussionen
Jag vill avsluta diskussionen av Murry Salbys ekvation med följande sammanfattande synpunkter.
Den stora diskussionspunkten har varit om det går att bevisa att det är en ren tillfällighet att Murry Salbys ekvation stämmer med observationerna. Den hypotes som flera diskussionsdeltagare har hävdat är att ekvationen stämmer av en matematisk tillfällighet därför att koldioxidkurvan råkar vara exponentiell. Jag hävdar att detta inte är bevisat, att Murry Salbys ekvation stämmer trots att koldioxidkurvan inte är exponentiell.
I figur 3 jämförs en exponentiell koldioxidkurva med den observerade koldioxidkurvan. Vi ser att den observerade koldioxidkurvan nästan sammanfaller med den exponentiella kurvan de första 90 åren. Därefter ser vi en stark avmattning i ökningstakten i den observerade kurvan men efter cirka 20 år kommer ökningen i gång igen och går då mot en mycket större ökningstakt än den exponentiella kurvan ger.
Detta bevisar att den observerade koldioxidkurvan inte är exponentiell. Men som vi ser i figur 2 så kan Murry Salbys ekvation ändå noggrant beskriva den konstanta ökningen av koldioxidhalten de sista 15-20 åren. Överensstämmelsen med observerade data är otroligt bra.
Slutsats: Att Murry Salbys ekvation stämmer med observationerna är ingen garanti för att den stämmer i verkligheten. Men överensstämmelsen de sista 15-20 åren är otroligt bra och kan inte förklaras med hypotesen att det är en matematisk effekt på grund av att koldioxidkurvan skulle ha en exponentiell form.
Uppdatering 2013-04-09
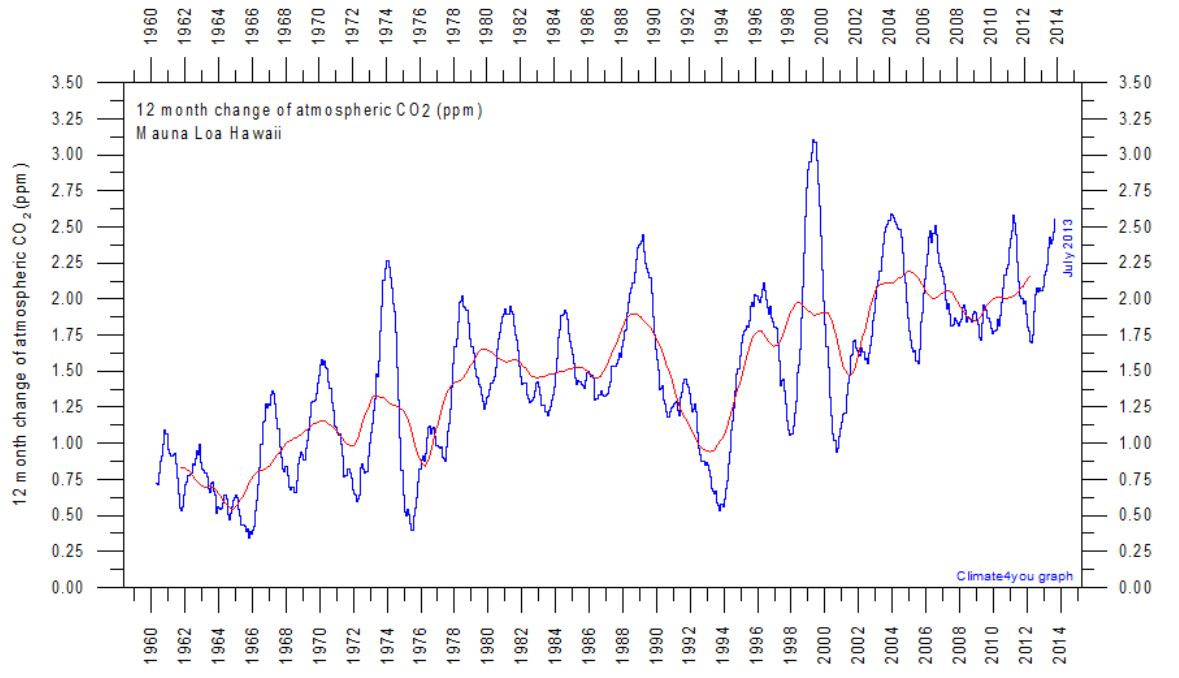
Jag har nu även testat Murry Salbys ekvation, ekvation (1) ovan, på Mauna Loas observerade värden för årlig ändring av koldioxidhalten. Dessa finns plottade på climate4you:
Dessa data kan betraktas som derivatan av koldioxidhalten dy/dt i ppmv/år och motsvarar alltså värdet på vänstra ledet i ekvation (1). Parametervärdena i ekvation (1) bestämdes till k = 2.21 och Tb = -0.415 genom parameteranpassningen enligt Figur 2 ovan.
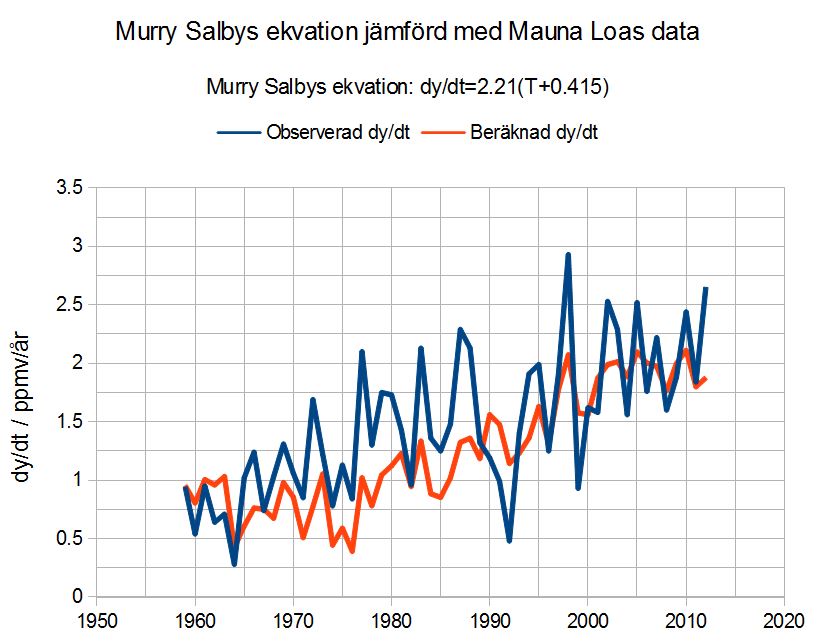
I följande figur har jag plottat Murry Salbys ekvation beräknad med ovannämnda parametervärden och HadCRUT4 för temperaturen som beräknad dy/dt medan observerad dy/dt är Mauna Loas data plottade årsvis.
Murry Salbys ekvation övergripande form stämmer ganska bra med observationerna. Varken beräknad eller observerad kurva visar tendenser till en underliggande exponentiell form (vilket har diskuterats livligt på sistone).
Men det är stora systematiska avvikelser mellan beräknade och observerade värden. Murry Salbys ekvation hänger inte med i svängarna när koldioxidhalten varierar uppåt och nedåt under inverkan av till exempel ENSO.
Det är dock anmärkningsvärt att Murry Salbys ekvation ändå återger så mycket av dessa förändringar på en kortare tidsskala. Man ser toppar och dalar i de beräknade värdena på de flesta ställen där det finns toppar och dalar i observationerna. Skillnaden är att Murry Salbys ekvation ger alldeles för låga toppar och för grunda dalar.
Anmärkningsvärd är också den bättre överensstämmelsen mellan beräknade och observerad värden som vi ser de senaste 15-20 åren om vi bortser från att Murry Salbys ekvation inte hänger med i svängarna (jämför motsvarande överensstämmelse i Figur 2 ovan).
Jag kommer i ett framtida blogginlägg att återkomma till ytterligare diskussion av dessa saker i samband med den ekvation av Gösta Pettersson som motsvarar Murry Salbys ekvation.
Referenser
Björnbom, 2013. Om Murry Salbys ekvation.
R. Wanninkhof med flera, 2013. Global ocean carbon uptake: magnitude, variability and trends. Biogeosciences, 10, 1983–2000, 2013.
www.biogeosciences.net/10/1983/2013/
doi:10.5194/bg-10-1983-2013









Hej
Eftersom jag inte känner Murray Salby så vet jag inte om han skämtar eller menar allvar. Jag skulle inte var förvånad om han skämtar.
För att lansera en trolig hypotes krävs nog litet mera. För det första måste man finna en rimlig förklaring var de antropogena utsläppen tar vägen? och för det andra måste man hitta en rimlig förklaring varför temperaturen ökar?. Att lansera denna hypotes nu förefaller extra besvärligt när nu temperaturen legat på en platå i ca 15 år! ( speciellt då havsytetemperaturen som man faktiskt kan mäta noggrant från satellit) och samtidigt som koldioxidutsläppen har ökat exponentiellt. Den exponentiella faktorn kommer i första hand, synes det mig, från de exponentiellt ökande utsläppen av koldioxid. Men det är ju bara en följd kanske av mitt enkla sätt att tänka.
LennartB
Formen på kurvan kan vara OK, men amplituden verkar konstig. Inte kan man få så stor temperatureffekt på ”jämvikterna”?
#1 Solinstrålningens trend har varit positiv. Kan inte detta vara den alternativa grundförklaringen? Att molntäcket då motsvarande måste ha minskat några få % kanske kan hänvisas till rent stokastiska processer i ett kaotiskt system. Det finns ju artiklar som pekar på att förhållandet temperatur och CO2 är en ”spurious correlation”. De mänskliga utsläppen behöver inte ”ta vägen” någonstans eftersom de ligger inom de naturliga flödenas felmarginaler och variationer. Enligt Murray skulle ackumuleringen av CO2 i atmosfären då mest bero på ”outgassing” från oceanerna pga av temphöjningen.
Aprilskämt?
Det förefaller vara rimligt att koldioxidens ökningshastighet i atmosfären bara beror på temperaturen. Den mänskliga emissionen av CO2 kan knappast vara drivande på något sätt, utan det är därför rimligt att anta att det är temperaturen som driver frisättning och bindning av den totala massan av CO2, inkluderande den antropogena. Men den primära drivfaktorn av dessa CO2-fluktuationer, måste vara solens energiflöde. Utan den fanns det ingen temperaturvariation att diskutera.
Pehr,
Tack för en rad intressanta inlägg om Salbys ekvation. Har du möjlighet att i korta drag redogöra för hur ekvationen är härledd?
Det är samtidigt konstigt att de modeller IPCC förespråkar inte tar hänsyn till någon form av avgasning. Det verkar ju vara direkt fel.
Hur de antopogena utsläppen av koldioxid påverkar halten i atmosfären beror väl på hur snabbt koldioxidöverskottet tas upp av haven.
Där har vi ju en stor kontrovers idag.
Gösta Pettersson hävdar i sin bok Falskt Alarm att uppehållstiden för koldioxid i atmosfären är så kort som c.a 7 år, medans IPCC talar om upp till 100 år.
G P publicerade en artikel om detta i WUWT, där han hävdade att mätningar av avklingningen av C14 isotoper i atmosfären efter att kärnvapenbombproven i atmosfären stoppats på 60-talet visar på en snabb relaxationsprocess.
Han fick en del mothugg i kommentarerna om att hastigheten på relaxationsprocessen inte går att läsa ut av omsättningshastigheten, så jag vet inte var det landar någonstans.
Kanske sanningen ligger någonstans mittimellan. Hastigheten i relaxationsprocessen är snabbare än IPCCs modeller, eftersom de inte tar hänsyn till avgasning medan den är långsammare än bombprovskurvans avklingning.
Det skulle göra Salbys teori intressant.
Lennart #1,
Hej Lennart, tack för tänkvärda synpunkter! Här kommer några funderingar om dessa.
Jag känner inte heller Murry Salby och att han skämtar är naturligtvis en möjlighet (men ett skämt med allvarliga konsekvenser för honom personligen, vilket talar emot). Vad kan det annars vara, kan det ses som visselblåsning (mycket populärt tema på sistone), jag vet inte? En person med stor social kompetens skulle nog resonera som så att även om hans ekvation stämmer så bra med observationerna så är frågan alltför känslig och farlig att ta upp, så att han lämnar till kolcykelforskarna själva att upptäcka detta. Men Murry Salby resonerade uppenbarligen inte så.
Att temperaturen ökar när koldioxidhalten ökar (oavsett orsak) anser jag är helt i linje med etablerad klimatvetenskap. Man anser ju till exempel att den naturligt ökande koldioxidhalten vid övergång från istid till mellanistid bidrar till temperaturökningen. Jämför också min modellering i denna fördjupningsrapport:
https://www.klimatupplysningen.se/wp-content/uploads/2013/06/Beräkning-koldioxid-temperatur.pdf
Då ser jag däremot invändningen från Thomas som ett större problem (även om det finns substansiella motargument), att med Murry Salbys ekvation så får vi ett instabilt klimat där temperatur och koldioxidhalt ökar utan slut, även om min beräkning tyder på att detta är en långsam process. En sådan instabilitet borde synas i proxydata för koldioxiden, men ser inte ut att finnas.
I frågan om var den antropogena koldioxiden tar vägen blir det naturligtvis frontalkollision mellan Murry Salbys ekvation och den etablerade kolcykelteorin. Men kollisionen beror på att enligt denna teori gäller att oceanernas försurning på grund av koldioxidökningen förhindrar vidare absorption av koldioxidöverskottet från atmosfären. Koldioxidabsorptionen går mer än tio gånger sämre på grund av denna försurning. Denna så kallade flaskhalsteori lades fram av Bolin och Eriksson 1959.
Om man resonerar som var allmänt vetenskapligt accepterat före Bolins och Erikssons teori så finns inget problem att förklara var den antropogena koldioxiden tar vägen. Den absorberas snabbt av havet och sprids ut bland kolreservoarerna så att endast en marginell andel blir kvar i atmosfären (för ett utförligare resonemang se mitt svar på ditt email från 23 juli).
Att Murry Salbys ekvation överensstämmer med observationerna skulle alltså kunna ses som ett tecken på att den etablerade teorin om hur oceanernas försurning hämmar absorbtionen av koldioxid inte ger en riktig bild. Men som jag betonat hela tiden så tar jag inte ställning till motsättningarna mellan Murry Salbys ekvation och den etablerade kolcykelteorin utan diskuterar bara utifrån mina egna förutsättningar hur dessa motsättningar ser ut och vad de kan innebära.
Björn-Ola #7 ”Det är samtidigt konstigt att de modeller IPCC förespråkar inte tar hänsyn till någon form av avgasning.”
Är du så insatt i de modellerna att du vet detta?
Peter #2,
Om man ser det hela som att koldioxidhalten i luften ökar på grund av att jämvikten mellan upplöst koldioxid i havsvattnet och koldioxid i luften ändras så är ändringen alltför stor.
Men om man i stället tänker sig att vi har ett komplicerat system i stationärt tillstånd som störs av en temperaturändring så är det i stället fråga om hur ett komplicerat nätverk av fysikaliska, kemiska och biokemiska processer ändrar hastighet på grund av temperaturändringen. Kan man då utesluta att den observerade ändringen är rimlig?
Jag har ett ganska stort problem med idén att kolcykeln (i teorin) skulle vara ngt fixt och konstant med väletbalerat jämvviktsläge(n) för transporten mellan de olika depåerna(*). Som skulle gå att bestämma genom er och bättre observationer. Det hela strider liksom mot all förståelse av hur naturen oc hdynamiska system där fungerar.
Jag har också problem med föreställningen att de olika processerna skulle vara temperaturoberoende och/eller synkrona
(*) På samma sätt som jag har ett stort probleme med föreställningen att där finns en ’rätt temperatur’ som råkade infinna sig precis innan CO2-utsläpp (och -halt) började öka påtagligt under säg tidigt 1900-tal.
Thomas P #9
Rätta mig gärna om jag har missuppfattat.
Björn-Ola #12 Jag har inte så bra koll på alla kolcykelmodeller, men om du hävdar att de inte har med en viktig faktor vore det väl lämpligt om du hade det? Det är lite väl vanligt på det här forumet att folk påstår ”IPCC ignorerar X” och när man kollar så ser man snabbt antingen att de har fel eller att de inte har en aning.
Visst Thomas … ungefär som man ju har med både haven och molnen också.Liksom dom som tvärsäkert hävdar att man visst har med både dem och molnbildning också.
Vet IPCC själva vad de har med? Eftersom man inte kan modellera en rad saker gör man parametriseringar, dvs gissar.
Dessa gissningar har inget direkt samband med fysikaliska lagar.
Thomas P #13
Jag utgår naturligtvis från det jag läst om detta. När du ifrågasatte så tänkte jag att du kanske hade någon annan källa som säger något annat.
Kunskap är inte hugget i sten.
Bern-modelen utgår från att koldioxidökningen är helt och hållet antropogen.
Björn-Ola #16″Jag utgår naturligtvis från det jag läst om detta.”
Och var har du läst det? I någon trovärdig källa?
”Bern-modelen utgår från att koldioxidökningen är helt och hållet antropogen.”
Eftersom vi släpper ut ungefär dubbelt så mycket CO2 som ökningen i atmosfären är det ett väldigt rimligt påstående. Kanske skulle, om vi haft en lika stor naturlig temperaturökning utan mänskliga CO2-utläpp halten ökat lite även då, men kan du säkert säga att så inte skulle ske även i Bern-modellen?
Om ökningen enbart beror på våra utsläpp, så förutsätter det en lång uppehållstid.
Där finns det en kontrovers.
Var det här kommer att sluta någonstans vet jag inte. Men Bernmodellen förutsätter en vattenlöslighet som är lägre än den jag har i min sodastreamer.
Återigen. Ett instabilt klimat pga. att CO2 följer temperaturen avgörs av
1. Nivån på Klimatkänsligheten(CO2) vilken kan diskuteras
2. Trögheten i kolsänkorna, främst havsoscillationer
3. Mängden CO2 som avges vid viss temp.ökning
Så på hela taget anser inte jag att frågan om instabiliteten är relevant om man inte har dessa frågor helt klart för sig först. Det kan visa sig att temperaturen ökar mot ett gränsvärde men sen är det stopp?
Pehr,
Har du några tankar om hur Bolins flashalsteori skulle kunna testas empiriskt? Känner du till om några sådana ansatser har gjorts?
En vetenskap på totalt gungfly!
Vi borde uppmärksamma vilken ”kultur” som gäller inom klimatvetenskapen jämfört med andra dicipliner. Det finns ett stort antal systematiskt återkommande bevis på hur klimatvetenskapen kvalitativt inte lever upp till vetenskapliga metoder. Det är helt enkelt en djävla lekstuga där de seriösa arbetena helt dränks i den kopiösa mängd ren kattskit som publiceras inom området. Med gubbar som Trenberth Jones och Mann i toppen för denna diciplin så kan det liksom inte bli mycket värre förutsättningar för vetenskapen bakom och under dem. när sedan det absolut mest substanslösa hysteriska artiklarna är de som når ut till folk med hjälp av journalister som ballat ur mer än IPCC självt, så finns det bara en part kvar att räta upp situationen och det är vetenskapen självt, där de som helgar de vetenskpliga metoderna får välja emellan om de vill dö enligt de villkor klimatgalenskapen dikterat eller återgå till de klassiska.
Det finns helt enkelt inga kvalitativa normer inom klimatvetenskapen och rätten till fri tolkning av data hämtade antingen från teoretiska modeller eller ur rent signalbrus från mätdata är rent häpnadsväckande och sanslöst ovetenskapligt. En kvalitativt normlös kultur inom fältet härskar och de som är seriösa och inte harklar sig kommer att få skylla sig själva för det här håller helt enkelt inte längre.
Björn-Ola #18 ”Men Bernmodellen förutsätter en vattenlöslighet som är lägre än den jag har i min sodastreamer.”
Tröttnar du aldrig på sådan där påståenden som du inte har minsta täckning för om vad IPCC eller Bernmodellen säger?
Jag har gjort en uppdatering av blogginlägget.
Michael #6,
Murry Salby har nog inte gjort någon teoretisk härledning av ekvationen. Han studerade sambandet mellan koldioxid och temperatur och kom på att ändringshastigheten av koldioxidhalten i atmosfären var proportionell mot en temperaturdifferens. Att hastigheten för mass- eler värmeöverföring kan beskrivas med en hastighetskoefficnt gånger en drivande kraft i form av en koncentrationsdifferens eller en temperaturdifferens är mycket vanligt som ett approximativt teoretiskt resultat inom teorin för mass- och värmeöverföring.
Michael #20,
Ett test av Bolins och Erikssons flaskhalsteori är att se efter hur mycket försurningen av oceanerna har påverkat den så kallade bombkurvan, dvs. minskningen av kol-14 i atmosfären efter det att de atmosfäriska kärnvapenproven upphörde. Detta har jag diskuterat i följande blogginlägg:
https://www.klimatupplysningen.se/2013/06/14/bombkurvan-igen-modell-och-observationer-stammer-inte/
Ett annat test är att undersöka hur snabbt nettoupptaget av koldioxid i havet är och speciellt hur det varierar med tiden. I artikeln av Wanninkhof med flera (2013) finns en jämförelse av beräknat upptag enligt kolcykelmodeller med uppmätta värden. Detta kan uppfattas som en test av flaskhalseffekten. Kolcykelmodellerna, som har flaskeffekten inbyggda, visar på en större försämring av koldioxidupptaget i havet än de uppmätta värdena.
Thomas P#22
Du får gärna föregå med gott exempel och förse din kritik med lite substans.
Björn-Ola #26 Du vräker ur dig påståenden som du inte kan belägga, och så fort jag frågar efter stöd för ett så hoppar du snabbt över till något annat, och efter alla dessa substanslösa påståenden begär du att *jag* skall komma med substans. Hur är det ens möjligt när du inte kommit med något substantiellt att bemöta? Du kanske kan imponera på andra ”skeptiker” med dina anklagelser mot IPCC och Bernmodellen, men vi som är lite mer skeptiskt lagda vill gärna se bevis.
Pehr #23 Förstår jag din uppdatering korrekt som att du menar att temperatur- och CO2- ökningen kan vara resultatet av en återkopplad process av exponentiell ökning utan yttre drivkraft, en spontant skenande växthuseffekt? Varför har vi i så fall inte sett liknande förut?
Det är inte så lätt att följa vad du menar ibland. Först säger du, helt korrekt att Lars Karlsson menar att Salbys ekvation kan stämma av en tillfällighet, men lite längre ned talar du om att ”inte motsäga Murry Salbys ekvation”. Salbys ekvation är en rent empirisk kurvanpassning, naturligtvis kan man inte motsäga den i det tidsintervall för vilket den skapats, allt man kan göra är att som Lars konstatera att det inte är så förvånande att anpassningen fungerar givet de CO2-utsläpp vi haft.
Jag väntar fortfarande med spänning på att du skall föreslå hur Salbys ekvation skall kunna falsifieras eller hur man kan testa den på något sätt, du vet, göra lite vetenskap av det hela.
Jonas N #11

Du har ju naturligtvist helt rätt i dina funderingar.
Det är närmast perverst att basera utgångsläget med konstant 280 ppm co2 i atmosfären och historiskt stabil temperatur. Det är ju faktiskt en helt oseriös utgångspunkt för klimatanalys.
Hela CAGW-förfarandet handlar ju om att man låtsas om att naturen skulle vara en konstant i total harmoni och att människan rubbat det gudomliga jämviktsläget…
Det är naturligtvis inte sant hur gärna många framstående forskare och meteorologer (som gärna hänvisar till förebilden Bohlin) och tar hans slutsatser som någon slags allsmäktigt bevis på hur spårgaserna skulle styra temperaturen och utan att vara det minsta intresserade av nyare hypoteser än dom som vann mark för hundra år sedan… Det är beklämmande hur konservativ de flesta forskarna tycks vara, och hur ointresserade man är av att ta del av nya tankesätt, inte minst ”vår egen” Lennart Bengtsson har visat prov på detta.
Kanske handlar det om klassiskt revir/statusmarkering inom akademikan, men nog är det trist och stelbent att fantasin och nyfikenheten tycks vara underordnad status och prestige och allmänt intellektuell stelhet. Men så har det väl och andra sidan alltid varit
Faktum är att ingen CAGW-förespråkare kan ge någon trovärdig förklaring till temperatur-dödläget trots linjärt ökad co2 i atmosfären. Hade dessa forskare varit det minsta hederliga hade man backat och kommit till den enda rimliga slutsatsen; dvs att klimatkänsligheten av ökad co2-utsläpp med all sannolikhet är betydligt mindre än vad som hävdats i AR4.
Gömt sig i djuphavet?
My ass!
Thomas #27,
Frågan om det instabila förloppet har vi ju redan diskuterat ad nauseam. Om vi bara kan observera en del av hela processen så kan denna framstå som instabil. Men delprocesser som vi inte för närvarande kan observera kan stabilisera utvecklingen i det långa loppet. Det finns gott om fysikaliska exempel som i en enkel teori ser ut att gå mot oändligheten men inte gör det i verkligheten. En fallande kropp ökar sin hastighet oavbrutet med 9,8 m/s2 enligt enkel teori men i verkligheten blir hastigheten efter ett tag konstant på grund av luftmotståndet.
I fråga om att Murry Salbys ekvation kan stämma av en tillfällighet så har jag nämnt detta redan från början, i mitt första blogginlägg om Murry Salby. Lars Karlsson har hängt på. I mitt första blogginlägg skrev jag:
Att Murry Salbys teori stämmer väl överens med observerade data är naturligtvis ingen garanti för att teorin också överensstämmer med verkligheten.
I mitt andra blogginlägg skrev jag :
Men som jag betonat och som vissa, som tydligen läser med polariserande glasögon, inte uppfattat, så påstår jag inget annat än att det inte är mer än en empirisk ekvation av vad vi vet idag.
För övrigt förstår jag inte vad du invänder mot i min uppdaterade text. Jag kan inte se att Lars Karlsson har tillfört något substantiellt, i och med att hans analys för det mesta är felaktig.
I fråga om att falsifiera Murry Salbys ekvation så påpekar du ju själv att det redan finns belägg för att den är sann. Så du gör din egen fråga meningslös. Om det är sant att en gråsparv är grå så går detta inte att falsifiera. Vi är ju överens om att Murry Salbys ekvation stämmer med observationerna, så det är inte fråga om att falsifiera detta.
Vad man sedan skulle kunna falsifiera är de hypoteser och teorier som skulle kunna föreslås som förklaring till Murry Salbys ekvation. Men det finns ingen forskning på detta så man kan bara spekulera om teorier och hypoteser. På detta stadium blir det därför meningslöst att diskutera falsifiering av tänkbara teorier och hypoteser eftersom dessa inte ens ännu föreslagits som förklaring i den vetenskapliga diskussionen om fenomenet Murry Salbys ekvation.
Björnbom förnekar sig inte. Han berättar inte att med en temp som ointegrerad ger R2 på 0,8 eller strax över mot CO2 så får jag efter integrering en R2 på 0,99. Ett R2 på 0,8 ger ganska stor utrymme för påverkan från andra faktorer.
Nåväl, jag har också prövat att dessutom lägga på en linjär trend (lutning 0,2) till temperaturen över hela perioden. När trenden är positiv blir det praktiskt ingen skillnad; när den är negativ så blir R2 innan integrering så lågt som 0,5, men efter integrering så hamnar den för det mesta på 0,98-0,99.
Så jag har en detaljerad förklaring som går att testa, och som klarar testerna.
Björnbom däremot har bara armviftande och vilda spekulationer med hål stora som månkratrar, som går emot ett halvt sekels forskning om kolcykeln.
Ha en trevlig helg.
Naturen och naturfenomen brukar uppvisa en förbluffande likformighet när man betraktar fenomenets delar och sedan delarnas delar o.s.v. (Se fraktalteori, kaosmatematik).
Salbys ekvation (1) exemplifierar detta; när istid övergår till varmare period, när vinter går mot sommaren och när natt blir dag. (Referenstillsånd istid, årstid och dygn). Då uppför sig koldioxidhalten enligt Salbys ekvation (1).
(Rätta mig om jag har fel.)
Jag är medveten om att detta inte är en förklaring. Lika litet som solcyklar förklarar temperaturförändringar. Men märk att även naturlagarna är beskrivande till sin natur.
Vi har upptäckt lagbundenheter som vi matematiskt har formaliserat. Detta innebär inte att vi fått en deterministisk förmåga att se in i framtiden, inte ens stokastiskt.
”Koldioxiden är den enda möjliga förklaringen till den globala uppvärmningen” förklarade en professor i meteorologi under ett statistikermöte för några år sedan. Professorn utgick således från att det måste finnas en förklaring, och inte bara det; han utgick också från att vi skall ha förmågan att hitta den.
Själv tror jag att den håller sig dold bakom komplexitetens oändligt tjocka brandmur.
Pehr #29 ”Frågan om det instabila förloppet har vi ju redan diskuterat ad nauseam”
Så länge du envisas med att skriva snarlika inlägg om Salby kan du knappast bli förvånad över att även motargumenten är snarlika. Du envisas med din vanliga undanflykt att Salbys ekvation *enbart* gäller perioden 1850-2011 och att utanför detta intervall precis vad som helst kan hända. Uppdelningen i långa och korta intervall håller inte eftersom även tidigare perioder kan delas in i sekellånga intervall och vi borde sett liknande där om det hela är en självgående process. Försök i alla fall kvalitativt att fundera på en mer komplett teori som inte motsägs av historiska data!
”I fråga om att falsifiera Murry Salbys ekvation så påpekar du ju själv att det redan finns belägg för att den är sann. Så du gör din egen fråga meningslös.”
Den är sann som beskrivning av perioden 1850-2011 för vilken den bara är en kurvanpassning. För att kunna kallas vetenskap måste den kunna göra någon form av förutsägelse som går att falsifiera. Ta T^4 formeln från svartkroppsstrålning som du tidigare drog upp som en framgångsrik kurvanpassning. Den härleddes i ett visst intervall men senare kunde man verifiera att den stämde även för högre och lägre temperaturer, dvs den hade prediktivt värde.
”Om det är sant att en gråsparv är grå så går detta inte att falsifiera.”
Nej, men om man säger att individer av arten ”gråsparvar” är gråa (bortsett möjligen från enstaka mutationer) så har man gjort en utsaga som går att verifiera genom att observera andra fåglar än dem man hade för att skapa sin hypotes. Det är den formen av generalisering som gör det till vetenskap och det är den formen av generalisering som du konsekvent vägrar göra.
”Vad man sedan skulle kunna falsifiera är de hypoteser och teorier som skulle kunna föreslås som förklaring till Murry Salbys ekvation.”
Om det fanns några sådana så skulle man kunna göra det. Försöker man göra en enkel sådan, som t ex den jag föreslog tidigare, så finner man dock snabbt att de strider mot gjorda observationer.
Johan E #31 Visserligen varierar CO2-halten med istidscykeln, men effekten är mycket mindre än den vi ser idag, om det nu vore så att CO2-ändringen beror på temperaturen. Det naturliga om något liknande Salbys ekvation vore sant vore tvärtom att effekten skulle vara större ju långsammare temperaturändringar vi har. Förändringarna under istidscykeln kan inte ha någon som helst likhet med denna Salbys ekvation.
Inte heller fungerar Salbys ekvation för årstidscykeln. CO2-halten varierar periodiskt under året vilket man inte kan säga att globala medeltemperaturen gör. Än sämre fungerar den för dygnscykeln där vi omöjligt kan ha någon variation på den globala CO2-halten.
”Men märk att även naturlagarna är beskrivande till sin natur. ”
Naturlagar är det till skillnad från Salbys ekvation som inte ens är det. Den är en kurvanpassning som bara fungerar för perioden 1850-2011.
Om man betänker all den möda som UI/Lars Karlsson och Thomas Palm lägger på att kritisera Salbys ekvation får man en känsla av att Salby är något viktigt på spåret.
Om man dessutom läser Karlssons inlägg med papper och penna i hand inser man snabbt att det handlar om rent svammel, något förvånande med tanke på Karlsons bakgrund. Men jag antar att syftet är att förstärka övertygelsen hos den CAGW-troende skaran, och då spelar resonemangets substans mindre roll. Även detta förhållande leder till att Salbys ekvation framstår som alltmer intressant.
Ledsen att behöva säga det, men Thomas Palms enorma ansträngningar att kritisera inläggen i denna blogg (i regel utan att tillföra något av intresse) och att sabotera diskussionerna med bloggtrollsteknik får därför en verkan rakt motsatt den avsedda. Hur orkar du, varifrån får du din energi?
Jag är en trogen TCS-läsare som också hela tiden stärks i min AGW skepsis tack vare TPs och UIs sätt att agera. Ger man dem rep vill de gärma hänga sig…
Thomas P #33 och andra,
Årstidscykeln av CO2 beror väl på nedbrytning av biomassa, vilket på årsbasis borde vara relaterat till global medeltemperatur då högre temperatur medför bättre tillväxt, men detta är förstås helt irrelevant för dygnscykeln, där väl CO2 inte varierar (?) trots stora temperaturskillnader. Årstids-variationen av CO2 är ju inte relaterad till nivån på fossilförbränning.
Finns det inga data på årstids-variationen för CO2 över land på södra halvklotet, den del som är beroende av biomassan borde ju vara invers mot norra halvklotets. Globala medelvärden är förstås mest beroende av norra halvklotet som dominerar landmassan.
Hej Thomas P # 33
Du bollar med begreppet ’global medeltemperatur’. Det är ett olyckligt begrepp. Statistiskt är det varken valitt eller reliabelt. Vad mäter det?
Dessutom är datat plockat från icke-stationära serier vilket innebär att slutledningarna blir, eller åtminstone borde bli, ytterst mediokra och försiktiga.
När det är vinter på norra hemisfären har vi sommar på den södra. Om vintern blir en grad kallare och sommaren en grad varmare så ger det inte utslag på medeltemperaturen? OM vi skall ha ett mått på klimatförändringen så bör det vara ett spridningsmått. Det skulle notera förändringarna.
Tillbaka till Salby (1) och referenstillstånden istid, årstid och dygn.
Jag vidhåller att ekvationen stämmer för de tre fallen. Du säger t.ex. ”CO2-halten varierar periodiskt under året”. Det är just detta jag också vill framhålla. CO2-halten varierar också periodiskt under dygnet.
Allt det här finns inbakat i Salby (1).
Thomas, om du väljer mina referenstillstånd och glömmer det där med ’global medeltemperatur’ och 1850-2011, så kan du tänka dig vara ense?
Hej Gunnar Juliusson # 36
På natten sker ingen CO2 upptagande fotosyntes. CO2 halten stiger på natten.
Johan E #37 Du säger ”Du bollar med begreppet ’global medeltemperatur’. Det är ett olyckligt begrepp. Statistiskt är det varken valitt eller reliabelt.” för att senare hävda ”Jag vidhåller att ekvationen stämmer för de tre fallen”. Globala medeltemperaturen dyker upp för att den är grunden i Salbys ekvation, det är inget jag ”bollar” med. Hur du samtidigt kan tro på denna ekvation och hävda att medeltemperaturen är irrelevant är som så mycket annat på denna blogg en gåta.
”Du säger t.ex. ”CO2-halten varierar periodiskt under året”. Det är just detta jag också vill framhålla.”
Vad har det med Salbys ekvation att göra? Vad har påstådda dygnsvariationer (som inte existerar i verkligheten i den globala bakgrundshalten av CO2) att göra med Salbys ekvation? Jag får ett intryck av att du i huvudtaget inte fattat vad denna Salbys ekvation är för något och var den skiljer sig från etablerade kolcykelmodeller.
#1 LB,
Trenden från 1850 visar ganska bra hur 60-årscykeln (från havsströmmar?) överlagras temperaturgrafen med en topp-topp amplitud på ca 0.4 grader. Dagens stationära temp sedan 1998 är ju 60-årscykelns ”nersida”. Efter 2030 överlagras trendens ”uppsida” den underliggande exponentiella trenden så att uppvärmningen tar fart med 1-1.5 grader fram till 2060 om expon.trenden (CO2) kvarstår. Elementär trendanalys. Salby jobbade med frekvensanalys för att isolera de periodiska förloppen.
Av alla har Tamino en hyfsad grafik över hur CO2 halten varierar över året på tre valda ställen
http://tamino.wordpress.com/2012/06/01/annual-cycle-of-co2/
Tre stationer, sydpolen, Barrows i Arktis och Mauna Loa.
Det som sticker ut är att sydpolens CO2 halt är i motfas trots att vid sydpolen ingen nämnvärd biologisk verksamhet finns pga kylan. Alltså är det närliggande områden som påverkar, och det är runt Antarktis bara hav. Det som jag uppfattar är att CO2 halten varierar med tillgången till kallt öppet vatten som kan absorbera CO2.
Barrow vid arktis: CC2 halten sjunker när isen försvinner. Eller om det beror på växtligheten. men landet runt Barrow är snöfritt innan havsisen släpper. Ändå följer CO2 halten havsisens schema. Inte snösmältningens.
Mauna Loa: CO2 halten följer passadvindens mönster exakt. Där växer det lika mycket året runt:
”During the summer months (May through September) wind speeds over the ocean exceed 12 miles per hour 50 percent of the time. Eighty to 95 percent of the time these winds are from the northeast quadrant.”
Från http://www.wrcc.dri.edu/narratives/HAWAII.htm
Det är menar jag, högst troligt att årstidsvariationerna i alla fall på dessa stationer beror till stor del på utbytet med haven, som i sin tur beror på tillgång till kallt öppet vatten, vind riktning och styrka och i haven brytande vågor.
Hej igen Thomas P #39
Min betraktelse gäller Salby (1) per se.
Naturfenomenet klimatet ser jag sedan på utgående från de (fraktala) referenstillstånden istid, årstid och dygn. I vart och ett av de tre fallen bör T och Tb anpassas till sitt referenstillstånd.
Thomas, kan du vara ense om Salby (1) förträfflighet nu i denna mera generaliserade och förklarade form?
Är det någon annan som ser detta i Salby (1)? Jag vet att jag har tagit upp detta fraktala istid-årstid-dygn resonemanget tidigare. Det var innan någon kände till Salby (1). Då väckte det inga kommentarer – eller kanske Thomas P kommenterade? Är det någon annan som nu känner sig manad?
Johan #42 Jag förstår i huvudtaget inte vad, om något, du menar. Det låter väl flummigt för mig.
43
Thomas P 2013/07/27 kl. 13:30 Thomas!Du har haft synpunkter på allt o alla!När skall du redovisa ”din” lösning på ett påhittat problem?
#43 och #42
I detta fall är jag nog benägen att tro Thomas P. Han har väldigt svårt att förstå saker och begrepp, argument, perpektiv mm som inte finns ’diskuterade’ i ymnig mängd på de sedvanliga alarmistsajterna. Detta gäller både den egna sidans argumentation och skeptiska invändningar och/eller annat relaterat till den vidare klimatdebatten.
Det är nog också ett av skälen till att han så ofta inte alls tycks kunna välja nivå när han skall anlägga moteld. Allt beksjuts med samma rasande frenesi av obarmhärtiga fördömanden. Och även de kakigaste av positioner på egna sidan skall försvaras med samma närmast blinda besatthet. Utan urskiljni
Hej Thomas P #43
Jag slutar där jag började #31: ”Naturen och naturfenomen brukar uppvisa en förbluffande likformighet när man betraktar fenomenets delar och sedan delarnas delar o.s.v. (Se fraktalteori, kaosmatematik).”
Låtom oss nu, utan att snegla på Salby (1), fraktalteori och kaosmatematik betrakta referenstillstånden istid, årstid och dygn. Vi tittar på temperatur- och CO2 kurvorna i samma figur för var och en av de tre tillstånden. Men dessa är nu med flit ritade så att skalorna inte framgår!
Vi kommer att ha stora problem att identifiera vilken figur hör till vilket tillstånd, ty figurerna uppvisar en förbluffande likformighet.
Thomas P
Skulle vara av intresse om Du redovisade vad som är problemet med klimatet!
Och redovisar hur Din lösning ser ut och skall göras!
Lennart #1,
Har du sett Salbys föreläsning på nedanstående länk? Man får inte direkt intrycket att han driver med sina åhörare. Jag har även läst hans senaste bok (Physics of Atmosphere and Climate). Den är synnerligen väl skriven och ger i alla fall mig intrycket att Salby måste tas på fullaste allvar.
Jag har nu även beställt Salbys tidigare bok (Fundamentals of Atmospheric Physics) som är avsedd för studenter på post grad-nivå. Det ska bli ytterst intressant att ta del även av detta verk.
Länk till föredraget: http://youtu.be/2ROw_cDKwc0
Att derivatan av koldioxiden map tiden är en funktion av temperaturen såg jag en härledning på för något år sedan. Det var en tråd på WUWT där Robert G Brown (rgbatduke) och Richard S Cortney hade ett långt meningsutbyte. Brown gjorde härledningen mot slutet av tråden, väckte nog egentligen ingen uppmärksamhet eftersom tråden var gammal och det bara var dessa två som hade ”fastnat” i tråden.
Borde ha bookmarkat.
I en annan tråd på samma forum, nu i vår, gjordes en plot av dy/dt och jämfördes med temperaturen med hjälp av Woodfortrees. Den stämde väldigt bra, men hittar inte det inlägget heller (grrr).
Gjorde ett försök men är inte så bra på WFT, kanske någon kan bättre.
Här integralen: http://www.woodfortrees.org/plot/hadcrut4gl/from:1960/offset:0.415/mean:24/integral/scale:0.221/offset:317/plot/esrl-co2/from:1960/mean:60
Och här derivatan: http://www.woodfortrees.org/plot/esrl-co2/from:1959/mean:12/derivative/mean:12/scale:1/plot/hadcrut4gl/from:1959/offset:0.415/scale:0.221/mean:12
Man kan nog normalisera och greja lite mer, den som plottade derivatan i WUWT-tråden lyckades iaf bättre än jag
Lars Karlsson #30,
Jag blir verkligen förvånad att du dyker upp här. Kul att du gjorde det i alla fall, alltid ett litet steg mot en mer skeptisk hållning i klimatfrågan. Om jag vetat att du varit här så skulle jag nog ha kommit hit och svarat tidigare trots sommarvärmen.
Jag är förvånad att du uttalar dig så tvärsäkert när det du har visat på UI i form av numeriska experiment inte är reproducerbart på grund av att det är så slarvigt presenterat.
Så länge du inte lägger fram dina resultat med rimlig vetenskaplig noggrannhet så att de går att reproducera så är det inte meningsfullt att diskutera dem.
Det allmänna resonemanget är enkelt. Om koldioxidkurvan är exponentiell och är enda externa forcing så ger den en temperaturkurva som är approximativt exponentiell som i sin tur kan ge tillbaka en exponentiell koldioxidkurva med Murry Salbys ekvation som kan sammanfalla med den ursprungliga kurvan. Om så vore fallet kan Murry Salbys ekvation överensstämma av en tillfällighet med koldioxidkurvan.
Vi antar nu att vi har andra externa forcings och naturliga variationer utöver koldioxidkurvan, precis som det är i verkligheten. Om koldioxidkurvan tillsammans med andra forcings åstadkommer en exponentiell forcingkurva (eller en exponentiell ekvivalent koldioxidkurva, där total forcing är omräknad till en tänkt ekvivalent koldioxidhalt som avviker från den verkliga) så får vi en approximativt exponentiell temperaturkurva. Men denna temperaturkurva skulle med Murry Salbys ekvation enligt matematiken ge tillbaka den ekvivalenta koldioxidkurvan, inte den verkliga. Det är därför din analys blir ogiltig.
Det vi ser från de verkliga observationerna är att temperaturkurvan avviker från exponentiell form (speciellt de senaste 15-20 åren) och att Murry Salbys ekvation ger oss den verkliga koldioxidkurvan som heller inte har en exponentiell form (koldioxidkurvan är linjär de sista 15 – 20 åren).
Så din förklaring att resultatet att Murry Salbys ekvation stämmer med observationerna på grund av att koldioxidkurvan och temperaturkurvan har exponentiell form håller inte.
Thomas #32,
Jag upplever att det nu har blivit någon slags rundgång i vår diskussion. Du vet vad jag anser och jag vet vad du anser och ingen av oss lär ändra sig i någon större grad av att samma gamla argument upprepas. Vi har konvergerat till ett sluttillstånd med andra ord.
Det enda som jag fann intressant att kommentera i det du skriver är detta med Stefans upptäckt av T4-formeln. Man kan läsa hans artikel här (på tyska):
http://www.ing-buero-ebel.de/strahlung/Original/Stefan1879.pdf
Dulong och Petit hade visat på en annan ekvation som också beskrev strålningen enligt experimenten. Men Stefan kunde visa att hans ekvation gav bättre överensstämmelse under vissa betingelser. Efter många år kunde Boltzmann visa en teoretisk härledning av Stefans ekvation och då var saken avgjord.
Om man tillämpar detta på Murry Salbys ekvation så kan man tänka sig att man i framtiden finner en teori som förklarar den. Teorin kan då också innehålla möjligheterna till att generalisera ekvationen så att vi får en förklaring till varför den ser ut att ge ett instabilt klimat. Den generaliserade teorin skulle då ge ett stabilt klimat och kunna förklara både proxydata och göra predikteringar.
Pehr #51 Man kan tänka sig mycket, men idag talar allt för att Salbys ekvation bara är ett slumpvis resultat av en kurvanpassning. Den har noll prediktivt värde, är inte falsifierbar, kan i nuvarande form omöjligt vara sann etc. Det finns vad jag kan se inte en enda punkt på vilken denna ekvation är överlägsen den existerande teorin. Återkom när du har något att komma med!
”Den … är inte falsifierbar”
”Det finns vad jag kan se inte en enda punkt på vilken denna ekvation är överlägsen den existerande teorin”
Är du riktigt på riktigt?
Pehr,
Jag har lagt upp ett förtydligande om experimenten i mitt inlägg.
”Men denna temperaturkurva skulle med Murry Salbys ekvation enligt matematiken ge tillbaka den ekvivalenta koldioxidkurvan, inte den verkliga. Det är därför din analys blir ogiltig.”
Frågan är inte om den integrerade temp-kurvan blir identisk med CO2-kurvan, utan hur stor likheten blir (efter anpassning). Och även om man lägger till fler termer kan man fortfarande få en stor likhet (R2 på 0,98 eller 0,99), beroende på vad de andra termerna (utöver CO2-kurvan) är. En del funktioner ger dock en sämre likhet.
Pehr, du kallar här ovan likheten mellan CO2-kurvan och temp-integralen för ”sensationell” (men utan att backa upp det med någon analys). Det är tydligt att den inte är särskilt ”sensationell”.
Förresten så är, som TP har påpekat, din anpassning av en exponentiell funktion till CO2-kurvan kass. Du tvingar den första punkten att ligga en bit över CO2-kurvan. Det är enkelt att få den att ligga direkt på.
Lars#54,
Dina resonemang om kurvanpassning är onitressanta eftersom de kan tillämpas på alla icke-stokastiska fysikaliska processer som låter sig beskrivas i matematisk termer. Vore det inte bättre att diskutera Salbys hypotes i en mer konstruktiv anda? Tänk om han är något på spåret?
Det är inte utan att man undrar över varför en ”kass kurvanpassning” föranleder sådant indignerat och rikligt utbyte av kommentarer. Pehr har upprepade gånger skrivit om denna ekvations grovt förenklade beskrivning av verkligheten samtidigt som det är märkligt att den faktiskt kan producera de resultat den gör. De mothugg Pehr får från Lars och Thomas (L&T) tycks mer vara ett behov att till varje pris visa att vad än Pehr skriver är det fel. Det är barnsligt och resulterar enbart till att ytterligare cementera vad respektive sida tycker om varandra. Jag skulle bli långt mer imponerad om L&T kunde beskriva de olika delmodellerna i GCM och hur dessa tillsammans med den totala systemmodellen validerats. Vilka är valideringsvillkoren, vilka antaganden har gjorts, etc. Jag tror att ett sådant konstruktivt bidrag på denna site skulle accepteras omedelbart och leda till en debatt mer präglat av ett mer konstruktivt meningsutbyte.
Lars K
Kudos för att du faktiskt vågar kommentera här. Synd att det är på den nivån du väljer. Men å andra sidan, skall man backa från en position där man totalt har låst in sig om att inga frågor är öppna längre, alla har besvarats, vetenskapen är avgjord och bara foliehattar (eller betalda lögnare) inte har övertygats ..
… då måste man förstås ändra riktning, dvs lägga in backen, och behöver att ta sig ganska (väldigt!) långt åt motsatt håll.
”Dumb as a bag of hammers” eller ’hur man beräknar medelvärden’ är inte metoder som funkar bland/inför intelligentare åskådare.
#52
nog har den ett prediktivt värde allt. Ponera att CO2-utsläppen stannar av till följd av finanskrisen men att temperaturen stiger och då även CO2, det skulle väl vara ett sätt att falsifiera eller använda den prediktivt?
Gustav #58 Man skulle kunna tro att den skulle kunna ha ett prediktivt värde, men eftersom ekvationen inte kan stämma om man försöker fortsätta bakåt i tiden före 1850 har Pehr valt att säga att den bara gäller för just den utvalda perioden och utöver det kan vi inget veta utan att ha en mer komplett (och helt okänd) teori. Det Tb han använder kan t ex inte ha någon mer allmän betydelse utan måste vara tidsberoende på något sätt, och så länge man inte kan säga hur kan man inte heller säga något om framtiden.
Thomas, slå upp svåra ord som ’falsifierbar’ och läsa på innan du försöker … det låter som om du har blandat ihop helt disparata begrepp, som tom (i sammanhanget) är ömsesidigt uteslutande.
Jag har gjort en ny uppdatering med en avrundning av diskussionen.
Tack för tillkommande kommentarer, speciellt Lars Karlssons och den uppdatering han gjort på sin blogg. Jag upplever dock att de olika argumentationslinjerna är uttömda och har därför avrundat för min del genom min egen uppdatering.
”Den stora diskussionspunkten har varit om det går att bevisa att det är en ren tillfällighet att Murry Salbys ekvation stämmer med observationerna.”
Från Pehr sida har det varit det, men en rimligare frågeställning är om man kan bevisa eller i alla fall göra troligt att det *inte* är en tillfällighet. Eftersom Salbys ekvation och parametrarna i den är utvalda för att passa är det naturligtvis i någon mening inte en tillfällighet att de också gör det. Hade inte nuvarande ekvation fungerat kan man hitta på andra och alltid stämmer någon.
Om den ”otroligt bra” anpassningen de senaste åren visar att Salbys ekvation är ”sann” vad bevisar då den sämre anpassningen 1905-1980? Inte nog med att Pehr kör med en kurvanpassning, han väljer sedan ut de intervall där kurvanpassningen fungerar bäst som bevis för hur bra den är!
Thomas #62,
Din kommentar är fylld med en mycket anpassningsbar gummiretorik. Vad du skriver går precis lika bra att säga om vilken teori som helst, till exempel anpassning av ekvationer inom kolcykelteorin på basis av hypotesen att koldioxidhaltens ökning är mestadels antropogen. Man kunde även säga samma sak om Stefans ekvation innan Boltzmann teoretiskt förklarade den och den blev Stefan-Boltzmanns strålningsekvation, men därefter var saken klar.
Pehr #63 Visst var Stefans ekvation bara en kurvanpassning när den tillkom. skillnaden var dels att den förväntades gälla utanför det intervall för vilket den var skapad, dvs den var testbar och dels att det vid tillfället inte fanns någon teori som kunde förklara svartkroppsstrålningen. En ren kurvanpassning var bättre än inget och gav i alla fall en ledtråd till vidare arbeta på att skapa en fungerande förklaring.Antag istället att någon idag plockade fram svartkroppsdata för ett begränsat temperaturintervall och lyckades göra en fin kurvanpassning till någon annan ekvation än T^4. En ekvation som han inte kunde motivera teoretiskt och han fick erkänna gav vansinniga resultat utanför detta intervall. Tror du någon skulle ta honom på allvar?
För kolcykeln har vi redan en fungerande teori och du har fortfarande inte lyckats klämma ur dig spår av förklaring till varför denna Salbys ekvation på något sätt skulle vara ett steg framåt.
Jag kan också avrunda med att berätta att jag har <a href=”http://uppsalainitiativet.blogspot.se/2013/07/bjornbom-bommar-igen.html”>testat</a> HadCRUT4 mot den exponentiella funktionen 4.7*(1.02**x – 1). Jag får R2 = 0,80 (eller 0,75 beroende på vilket håll man gör jämförelsen) för den ointegrerade HadCRUT4, och jag får R2 = 0,995 för den integrerade HadCRUT4. (Jag använder 2 parametrar vid anpassningen)
Jag får liknande resultat för syntetiska temperaturkurvor: från runt 0,8 till över 0,99. Så det är ingenting särskilt med integralen för temperaturen. Det verkar som att om man har en kurva som är exponentiell med ett hyfsat R2, så blir den exponentiell med ett mycket bra R2 efter integrering.
Salby har således inte upptäckt något som kommer att ha betydelse för vår förståelse av kolcykeln.
Thomas #64,
Kolcykelteorin kan ju inte ens förklara orsaken till att koldioxidhalten varierade mellan istider och mellanistider:
http://theclimatescam.se/2012/11/09/klimatets-mysterier/
Detta anser jag inte att man kan kalla en ”fungerande teori”. Det är fortfarande fråga om hypoteser som står på lösa grunder.
Lars Karlsson #65,
Efter att ha studerat din uppdatering på UI med närmare förklaring av dina beräkningar kvarstår min kritik från uppdateringen 2013-07-26 i blogginlägget ovan:
Men Lars Karlsson har i sitt resonemang och sina numeriska experiment gjort en fundamental miss som strider mot etablerad klimatvetenskap. Han förutsätter att enda externa forcing kommer från koldioxiden. Men enligt den etablerade klimatvetenskapen så påverkas temperaturen också av forcings från växthusgaser såsom metan och klorfluorkarboner och diverse aerosoler med mera. Hans analys håller därför inte.
Jag kan inte se att du någonstans har besvarat denna kritik.
Jag undrar också över din metod att beräkna temperaturen från koldioxidkurvan. Du använder formeln
T-T0=0,8*(ln(y/300))/ln(400/300) C (1)
Vad är tanken bakom att använda denna formel som ger en global temperaturökning av 0,8 C när koldioxidhalten stiger från 300 till 400 ppmv?
Normalt brukar det sägas att den globala temperaturen stigit 0,8 C när koldioxidhalten ökat från 280 till dagens nivå på cirka 400 ppmv. Då borde ekvationen i stället vara:
T-T0=0,8*(ln(y/280))/ln(400/280) C vilket motsvarar en klimatkänslighet på 0,8*(ln 2)/ln(400/280) C = 1,6 C.
Motsvarar detta din åsikt om klimatkänslighetens storlek?
Är du medveten om att med ekvation (1) så måste temperaturkurvan T-T0 av rent matematiska skäl få approximativt samma form som koldioxidkurvan y-y0? Detta följer av serieutvecklingen att ln(1+X) är approximativt lika med X när X << 1.
Men i verkligheten följer temperaturen inte ekvation (1). Denna är en mycket grov approximation och lämpar sig inte för ett resonemang om vad man kan dra för slutsatser från de olika kurvornas form. Temperaturkurvans form bör då, som jag antyder i ovannämnda kritik, i stället beräknas från antagna rimliga forcings (vars kurvform inte motsvarar koldioxidkurvan) med hjälp av en klimatmodell. Det enklast möjliga är då att använde den enkla energibalansmodellen (EBM) som jag brukar använda då och då.
Men som jag förstår din uppdatering på UI så har du inte använt någon annan metod än ekvation (1). Stämmer det?
Pehr,
(1) Jag har prövat att addera andra funktioner utöver koldioxidforcing till temperaturen, för att se vad som kan hända om det finns fler forcings. Se inlägget, och tidigare kommentarer här.
(2) Om vi lägger in de forcings som gav upphov till den faktiska temperaturökningen, så får vi naturligtvis en temperaturkurva som blir lik den observerade, och för den vet vi att vi får en bra anpassning av integralen mot CO2. Man skulle kunna uppskatta dessa forcings genom att filtrera temperaturkruvan och sedan skulle man kunna lägga på nytt brus, men detta kommer endast att ge marginell skillnad.
(3) Vilken faktor jag använder som ”klimatkänslighet” är helt irrelevant för hur väl den resulterande kurvan går att anpassa, och det är ju detta jag undersöker. Vid kurvanpassningen mot CO2 så skalar jag ju ändå om temperaturen.
(4) Som jag påpekade i min förra kommentar (och i en uppdatering i mitt inlägg) så följer den faktiska temperaturkurvan den exponentiella kurvan jag använder ganska väl. Den passar ungefär lika bra som de syntetiska temperaturkurvor som jag jag har använt i mina experiment.
Pehr #66 ”Kolcykelteorin kan ju inte ens förklara orsaken till att koldioxidhalten varierade mellan istider och mellanistider”
För att citera vad du skrev i den artikel du länkar till: ”Många processer, skriver man, har identifierats som skulle kunna påverka koldioxidhalten i atmosfären under istidscykeln. Men man påpekar också att de proxydata med vilka man kan testa de olika hypoteserna är relativt knapphändiga och osäkra och tolkningarna av dessa data står delvis i konflikt med varandra.” Visst har våra teorier brister när vi går tillbaka i tiden eftersom vi inte har tillräckligt med data-
Salbys ekvation eller rimliga expansion av denna för att få den stabil ger å andra sidan extremt fel svar eftersom denna visar på mycket större förändringar av CO2-halten än som observerats så du kan knappast hävda att den är någon förbättring. Jag får väl åter påminna dig att om en ny hypotes skall få genomslag måste den i alla fall på någon punkt vara bättre än existerande, och dit har du ännu efter jag vet inte hur många artiklar och uppdateringar nått.
Lars Karlsson #68,
I den av klimatforskningen accepterade teorin har vi:
Koldioxidkurva som inte är exponentiell + andra forcings och naturliga variationer som inte är exponentiella ger en temperaturkurva som inte är exponentiell. När man tillämpar Murry Salbys ekvation på temperaturkurvan får man fram koldioxidkurvan.
I dina experiment ser det ut att vara så här:
Koldioxidkurvan är exponentiell, temperaturkurvan beräknas från koldioxidkurvan med en grovt approximativ metod som har den matematiska egenskapen att den då blir approximativt exponentiell. Murry Salbys ekvation tillämpad på temperaturkurvan ger då tillbaka den exponentiella koldioxidkurvan, vilket också är en matematisk nödvändighet. Dessutom adderas AR3-brus både till koldioxidkurvan och till temperaturkurvan, oklart varför just AR3-brus används och varför detta skulle göra analysen bättre.
Vissa tillägg, exponentiella och linjära, adderas också till temperaturkurvan efter att denna har beräknats från koldioxidkurvan men innan Murry Salbys ekvation tillämpas. Oklart dock hur detta är tänkt och vad resultaten säger.
Jag kan inte se att du har bevisat de påståenden du gör om att Murry Salby stämmer med observationerna av en tillfällighet.
Thomas #69,
Murry Salbys ekvation, speciellt att den stämmer så bra med observationerna, har nyligen börjat diskuteras vetenskapligt. Jag har hela tiden upprepat att det inte är en garanti för att Murry Salbys ekvation stämmer med verkligheten att den stämmer med observationerna.
Men vi kan inte veta vad som kommer att hända i framtiden med Murry Salbys ekvation. Det är möjligt att denna ekvation, i samma eller modifierad form, kommer att inordnas i en framtida kolcykelteori som är klart bättre än dagens ofullgångna dito. Istiderna är bara ett av många luckor, en annan är det okända kolsänkan som finns med i analyserna som en tilläggshypotes (se Gösta Petterssons bok ”Falskt alarm”).
Varken du eller jag kan förutsäga hur det kommer att gå med detta.
Pehr, jag ska försöka förklara det här så enkelt som möjligt:
(1) Den observerade temperaturen (HadCRUT4) är lika exponentiell som mina syntetiska temperaturserier (runt 0,8).
(2) Både den observerade temperaturen och mina syntetiska temperaturserier blir efter integrering mycket nära exponentiella (runt 0,995).
Så vad är det som är så ”sensationellt” med den integrerade observerade temperaturen?
Lars Karlsson #72,
Det är fortfarande helt klart från figur 3 ovan att den verkliga koldioxidkurvan avviker markant från en exponentiell kurva.
Det är också klart från figur 2 att Murry Salbys ekvation stämmer bra med den verkliga koldioxidkurvan, speciellt är det sensationellt bra etter 1980 då vi har bra temperaturmätningar både från satelliter och från jordytan som överensstämmer med varandra.
Därför stämmer inte dina slutsatser. Gissningsvis har ditt sätt att okritiskt använda R2-värdena lett dig på villovägar förutom att det blir ett cirkelresonemang när du använder grovt approximativa ekvationer som matematiskt måste ge det önskade resultatet.
Ledsen Pehr, men nu hittar du bara på. Och dina ”anpassningar” är förvånansvärt dåliga.
Och jag slösar tydligen bort min tid.
Lars Karlsson #74,
Jag själv är inte ledsen, jag kom att tänka på rönnbär i stället
Skämt åsido, här kommer ytterligare en fundering.
Vi är eniga om att en exponentiell koldioxidkurva ger en exponentiell temperaturkurva (med den approximativa ekvation du använder för transformationen) som sedan ger tillbaka en exponentiell koldioxidkurva när man tillämpar Murry Salbys ekvation.
Då blir det ett cirkelresonemang när du i din analys utgår från en exponentiell koldioxidkurva för att bevisa att Murry Salbys ekvation ger observerad koldioxidkurva av en matematisk tillfällighet. Du bevisar ditt eget antagande.
Ditt problem är att undersöka om den observerade koldioxidkurvan avviker så lite från exponentiell kurva att dess överensstämmelse med observationer beror på en tillfällighet eller inte. Den analys du har gjort svarar inte på denna fråga.
Det är inte bara fråga om att den observerade koldioxidkurvans form liknar en exponentiell kurva. Det finns likheter i formen men också signifikanta skillnader.
Du måste kunna förklara varför det blir så bra överensstämmelse mellan observerad koldioxidkurva och den som beräknas med Murry Salbys ekvation under tiden efter 1980 då vi har de mest pålitliga temperaturobservationerna. Är detta en tillfällighet eller inte?
Hur som helst så kan det vara så att graden av överensstämmelsen mellan Murry Salbys ekvation och observerad koldioxidkurva, på grund av singulariteten vi får om koldioxidkurvan skulle vara exponentiell, blir ett trubbigt mått på förhållandet mellan hur mycket av koldioxidökningen som är antropogen och hur mycket som är naturlig. Gösta Pettersson har med en annan modell (se paper 3) kommit fram till att den antropogena andelen är knappt hälften så att mer än hälften av den ökade koldioxidhalten i atmosfären beror på naturliga orsaker.