Ett av klimatvetenskapens antaganden är att det finns en klimatkänslighet. Med betoning på en. Ändras tillförd energi till jordytan så ändras den globala temperaturen. En viss mängd energiförändring innebär samma temperaturförändring, oavsett vad mängden energi och den globala temperaturen var från början.
Det finns anledning att ifrågasätta detta antagande. Kanske är temperaturförändringen inte en linjär funktion av energiförändringen?
En av dem som ifrågasätter, är Willis Eschenbach, flitig skribent på världens mest besöka klimatsajt, WattsUpWithThat. Han har nu skrivit ett nytt inlägg om vad mätningar visar. Mätningar som i det här fallet är BESTs temperaturserie och CERES’ mätningar av energiflöden i atmosfären.
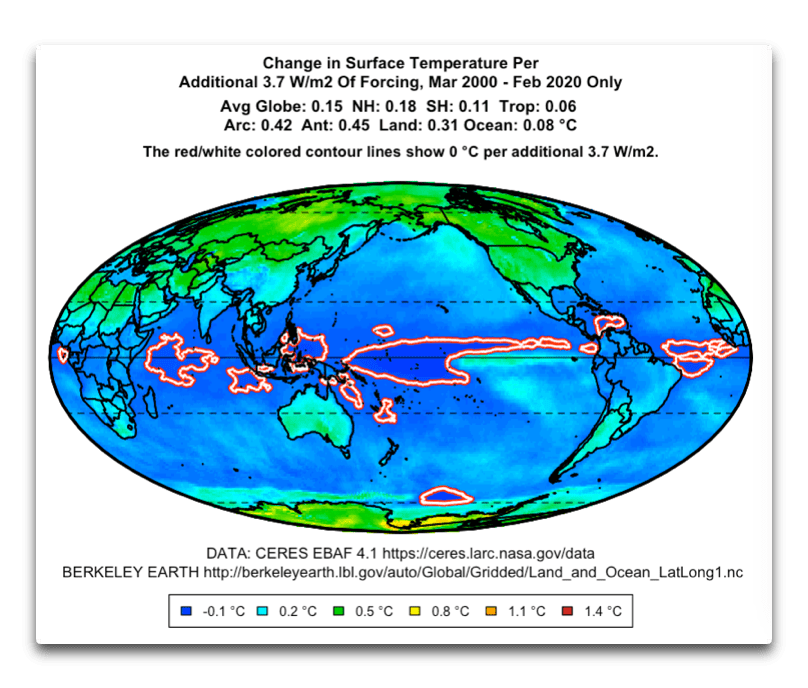
Ett resultat är kartan ovan. En karta som visar sambandet mellan förändringar i energi (eller egentligen i effekt per ytenhet) och temperaturförändring, där data är indelade i rutnät över jordytan. Eschenbach har räknat om de verkliga temperaturförändringarna till vad de skulle bli om förändringen i effekt hade varit 3,7 W/m2 (och om sambandet är linjärt i varje ruta). Det värdet är valt för att det är allmänt accepterat att en fördubbling av koldioxidhalten medför en sådan förändring av energiflödet i genomsnitt.
Som framgår av kartan, är temperaturförändringen inte densamma för varje ruta, inte ens för rutor på samma latitud. Uppenbart är också att det är stor skillnad för havsytor och landytor, där de sistnämndas temperaturer reagerar mer när tillförd effekt ändras.
Nära ekvatorn finns stora havsytor där sambandet mellan effekt och temperatur till och med är det motsatta vad man skulle tro. När tillförd effekt per ytenhet ökar, minskar temperaturen! Vilket sannolikt beror på den motverkande återkoppling som Eschenbach anser sig ha upptäckt. En återkoppling som består i att det bildas tropiska åskväder när tropiskt havsvattnet värms upp. Om uppvärmningen går snabbare, skapas åskvädren tidigare på dagen och hindrar mer uppvärmning. Åskvädren kyler, både genom att de tjocka molnen skymmer solljus och genom att åskan och regnet i sig för bort energi från atmosfären.
Eschenbach har skrivit om denna troliga, motverkande återkoppling flera gånger, senast här. Där ber han också om förhandsgranskning av en vetenskaplig artikel som han planerar. Vilket är en bra idé. Är det inte publicerad som en förhandsgranskad, vetenskaplig studie räknas det inte. Ja, många klimatforskare och många av IPCC:s skribenter anser nog att det inte ska räknas ändå. Det motsäger ju att det skulle vara någon klimatkatastrof på gång.
Är det någon läsare som anser sig kunnig, finns här chansen att bidra lite till klimatvetenskapen.
Den enklaste klimatmodell som går att göra, är att smeta ut all effekt till jordytan jämt över den, och sätta att den globala medeltemperaturen råder överallt. Det är verkligen ingen realistisk modell, men kan säga lite grann om hur klimatet fungerar. För sambandet mellan effekt och temperatur brukar så Stefan-Boltzmanns lag användas. Den gäller visserligen för svarta kroppar, men genom att lägga till en konstant fås den att gälla för en grå kropp. En grå kropp ser inte nödvändigtvis grå ut, utan kallas så för att utstrålning och absorption följer planckkurvan multiplicerat med samma konstant (mindre än 1), oberoende av våglängd. Därmed har den inga spektrallinjer. Jordytan och jordatmosfären är inga grå kroppar, men det här handlar om en väldigt enkel klimatmodell.
Eschenbach visar i sitt inlägg att jordytan och jordatmosfären avviker ganska rejält från Stefan-Boltzmanns lag, och därmed från den där enkla klimatmodellen. Temperaturen ändras betydligt mindre än vad den ”borde”.
Analysen utesluter i och för sig inte att det finns en klimatkänslighet globalt. Men sannolikt finns det inte någon linjär, global klimatkänslighet. Ta bara dessa stora områden där temperaturen sjunker när energiflödet ökar. Om dessa områden ökar när energiflödet ökar ännu mer, sjunker ju klimatkänsligheten. Och tvärtom ökar den då när energiflödet minskar.
En av de få saker som klimatforskarna är överens om, är att en fördubbling av koldioxidhalten, med allt annat oförändrat, leder till en global uppvärmning på cirka en grad. Eschenbach visar i två diagram att sambandet inte verkar vara linjärt, utan är långsammare. Han kommer fram till klimatkänsligheten är betydligt mindre än en grad per fördubbling av koldioxidhalten. Hans värden ligger nära vad Richard Lindzén anser vara riktigt, baserat på den iriseffekt han har upptäckt. Storleken på iriseffekten har i och för sig ifrågasatts av andra forskare, men knappast att den alls existerar.
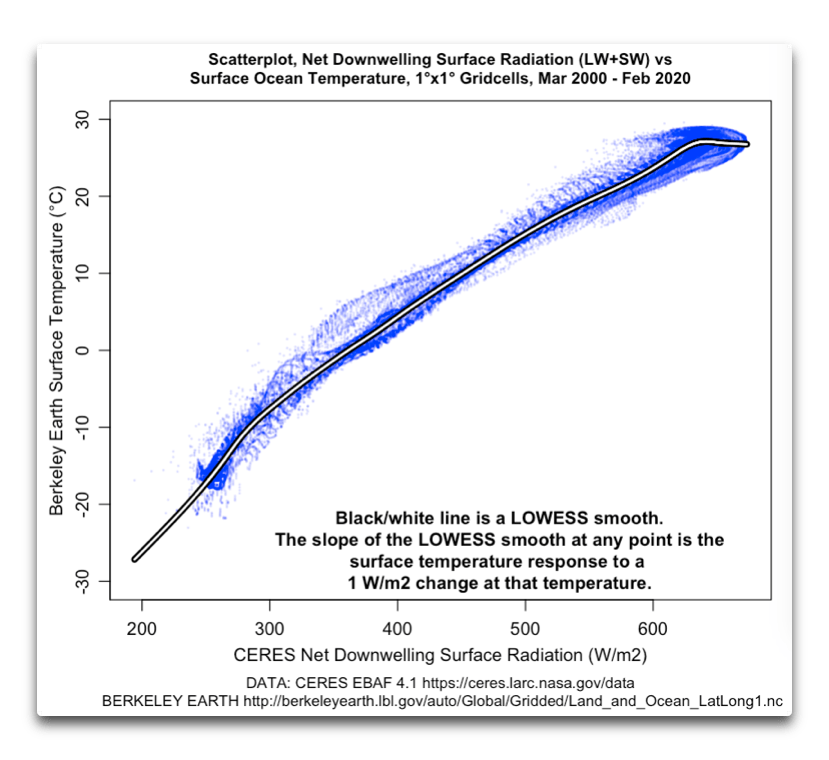
Om klimatkänsligheten ligger långt under en grad för varje fördubbling av koldioxidhalten, finns det naturligtvis ingenting att oroa sig för när det gäller koldioxidutsläpp och klimatförändringar. En så liten global uppvärmning har huvudsakligen, eller kanske bara, positiva effekter. Än mindre anledning finns att oroa sig, om klimatkänsligheten minskar när koldioxidhalten (eller i varje fall tillförd effekt) ökar. Vilket Eschenbachs analyser tyder på, exempelvis genom detta diagram för världens oceanytor:








Vetenskapligt sett så är det en stor gåta varför inte klimatforskningsområdet som sådant har sett till att klmatkänsligheten har studerats mer ingående. Efter 40+ år ar studier av allt möjligt annat – främst via modellbyggande och simuleringar, så har vi inte kommit en tiondels grad närmare ett användbart värde.
Mer av studier lika Eschenbachs åt världen, och mindre av RCP8.5-baserade simuleringar av framtida katastrofer! Det är jag beredd att lägga pengar på.
”Kanske är temperaturförändringen inte en linjär funktion av energiförändringen?”
Exakt ! Man kan verkligen undra varför den skulle vara det?
”Klimatvetenskapen” har ju bara påstått att det skulle vara så. De har aldrig visat att det är så.
Eschenbach pekar ju på något helt fundamentalt.
Om instrålningen ökar så ökar jordens förmåga att göra sig av med det tillskottet (genom ökad reflektion och ökad konvektion = högre utstrålning från atmosfären).
Yttemperaturen behöver inte öka, bara för att instrålningen (från toppen av atmosfären) ökar.
Det finns andra sätt för jorden att göra sig av med tillskottsenergi.
Tycker att Eshenbachs (och Lindzens) modeller stämmer bra med att jordens temperatur är förbluffande stabil.
Begreppet klimatkänslighet borde aldrig ha introducerats. Det är föga vetenskapligt intressant av den enkla anledningen att det inte kan valideras eller för delen falsifieras. Orsaken är att jorden aldrig befinner sig i termisk jämnvikt på grund av att haven har en avsevärt längre tidsskala än strålningsvariationerna.
Det är mer meningsfullt att observera hur temperaturen i atmosfär och hav ändras över tid. Här finns nu tillförlitliga observationer för cirka ett halvsekel samt ett begränsat antal meteorologiska mätningar för upptill 200 år.
Allt övrigt är indirekt information med mer begränsad tillförlitlighet än de flesta vill erkänna.
Vill man så att säga hålla sig på jorden eller i verkligheten är det vetenskapligt mer meningsfullt att mer i detalj studera vad som hänt de senaste 40-50 åren.
#3 L.B. Jo kanske, men är det inte väl svårt att skilja klimat pga. CO2 från olika oscillationer i så kort tid?
#2 Jonas. Självfallet är det inte linjärt. Instrålningen är kanske tämligen linjär, men utstrålningen prop. mot fjärde potensen av temperaturen. Till det kommer ändring av albedo mm.
Tack Lars K
Willis E är en produktiv amatör som kan bolla med datan.
Hans Thermostatteori är baserad på studier av moln vid ekvatorn-där han bodde .
Att få upp den i en erkänd tidskrift är en bra ide.
Kan bara återupprepa vad Lennart B visade i ett inlägg här tidigare ang globalstrålningens förändring under 40 år:
Globalt +-0,00 W/m2
Globalt hav -0,34 W/m2
Globalt land +0,85 W/m2
Europa land +2,0 W/m2
Mellan Sverige +1,2 W/m2
Vad jag förstod var detta en 10 årstrend så allt skall fyrdubblas!
Globalt land 3,4 W/m2 således.
Molnen har en stor betydelse. Inte bara över ekvatorn när de bildas på em.
#3 Lennart Bengtsson
Ja, det är bara att hålla med dig om klimatkänsligheten vilken inte går att vare sig verifiera eller falsifiera. Men den ramar in hela frågeställningen på ett enkelt sätt; hur blir temperaturförändringen vid en viss ökning av växthusgaserna. Så jag kan förstå att begreppet röner intresse. Tycker du att TCR har bättre relevans?
Ang. observationer så är vi nu uppe i 500 ppm CO2e (2019) vilket är c:a en 80%-ig ökning jämfört med de 278 som sägs ha funnits 1750. Vi är alltså inte så långt från en dubbling så vi kan snart se vad detta ger för temperatureffekt (minus långtidseffekterna som sägs komma innan vi hamnat i jämvikt.)
Bra Lars att du tar upp detta inlägg. Jag gjorde en liknande övning 2014 där jag tittade på hur solinstrålningen ändrades under årstidsväxlingarna för norra och södra halvklotet. De siffror jag kom fram till då stämmer mycket väl överrens med de siffror Eschenbach räknar fram. Här är min rapport:
https://mcederlof.se/onewebmedia/seasonal_variations_0_6.pdf
Det var en gång ett folk som var väl bekant med vatten men aldrig lyckats värma det till högre temperatur än 95 C.
Så en dag kom deras vetenskapsmän på hur de skulle kunna hetta upp det ytterligare ( men den just nyligen uppfinna elden). Oj vad förvånade de blev när det vid 100 C plötsligt inte blev varmare utan mystiska bubblor började uppträda. Inte bara olinjaritet i temperatur kurvan utan t.o.m. kaosförlopp i vattnet.
Så länge vi inte vet hur stora de naturliga klimatförändringarna är så är det meningslöst att försöka uppskatta de av människan orsakade klimatförändringarna är. Genom att sätta de naturliga klimatförändringarna till noll eller nästan noll får man det resultat som IPCC eftersträvar. Jag förmodar att klimatmodellerna (varför behövs mer än EN) inte kan uppskatta de naturliga klimatförändringarna genom att sätta koldioxidhalten konstant.
Behövs det verkligen mer räknande? Är det inte bättre att använda historiska källor och studera vad som verkligen hänt med klimatet genom årtusendena? Det finns ju mängder med data både från borrkärnor och skrivna dokument till fossil och annat att ta till! IPCC har ju visat att modeller och beräkningar av klimatet blir bara skit och har inget med verkligheten att göra…Men räknenissarna har bråda dagar antar jag!
”Ett av klimatvetenskapens antaganden är att det finns en klimatkänslighet. Med betoning på en.”
Det är väl både rätt och fel. Om den är linjär så vet vi att förhållandet är 1,6 (390/240) mellan utstrålningen vid ytan och toppen av atmosfären. Det skulle innebära att en fördubbling av koldioxid medför en sammantagen forcing med 5,9 watt vid jordytan vilket motsvarar drygt en grad. Så man förutsätter egentligen en ökad klimatkänslighet på marginalen, bl.a. att tillkommande vattenånga absorberar ytterligare 2w/m2/K.
Lars, ”klimatkänsligheten” är en av de riktigt stora bovarna i klimatfrågan eftersom Charneygruppens gissningar, så vitt jag förstår, ligger till grund för berättelsen om ”klimathotet”.
Om jag har förstått Lindzens hypotes om iriseffekten rättså skulle den, om den bekräftades, kunna påverka beräkningarna så att ”klimatkänsligheten” blir mycket nära noll. Hans hypotes har varit mycket omstridd, kanske motarbetad är bättre uttryck, men verkar på senare tid ha kryat på sig.
I Climate Change The Facts 2020 har Lindzen själv skrivit en liten artikel ”reflektion on the iris effect”.
Någon som vill kommentera?
Magnus C#7
Vilken intressant modell du hade redan 2014.
(Ju enklare modell ju bättre : )
OT
Såg ett program som heter Mutantväder på en TV-kanal. Det handlade om svåra vinterstormar i USA och Kanada. Man skyllde på ökningen av koldioxid och ”global uppvärmning”. Människans utsläp är skulden är budskapet. Extrema väderhändelser blir allt värre påstås det.
#7 Magnus C
Snygg rapport!
UAH data brukar visas upp tillsammans med modellernas utfall.
De går lite heta!
Det vore kul med en graf med din modell att jämföra med.
Du kan ju få forcing från Lennart Bs siffror ovan.(#5) eller har jag förstått fel?
Problemet med klimatkänslighet som beskriver förändringar på temperatur eller W/m2 endast är en funktion av CO2. Alla övriga interna, externa och antropogena faktorer som påverkarklimatet försummas. Där den antropogena mentala faktorn har den alvarligaste negativa effekten på livsmiljön. Vår fantastiska hjärna tillåter oss inte att gå stadigt in i framtiden, men den låter oss åtminstone förstå vad det var som fick oss att snubbla. Det är därför de unga måste ta lärdom av de gamla och erfarna innan de förtar sig. Det verkar som att de flesta organisationer, religioner, makthavare och politiker har tappat både kartan och kompassen och står under CO2 lyktan för att söka efter den stora klimatomställningen. Men jag hoppas fortfarande att de visa att göra listan på de kloka åtgärderna som behövs.
#13 Sten Kaijser
Efter alla dessa år har jag faktiskt inte hittat nåt argument som gör att man inte skulle kunna räkna på det här sättet. Och ja, ju enklare desto bättre.
#15 Lasse
UAH uppvisar mycket större uppvärmning än vad jag och Eschenbach räknar fram. Men det finns ju helt naturliga uppvärmningsorsaker också.
#10 Benny. Håller med Dig om att det är bra mkt smartare och klokare att studera och försöka förstå uppmätta (väder-) variabler än att lägga stora belopp på att förutspå (modellera) möjliga framtida värden av samma variabler.
Klimatkänslighet tillför inget av värde, modeller gör det men bör aldrig presenteras utan tydliga felmarginaler.
Observationer absolut. Särskilt med väl tilltagna glidande medelvärden
https://www.woodfortrees.org/plot/hadcrut4gl/mean:720/plot/hadcrut4gl/mean:132
men även rekonstruktioner så vi ser
var vi har varit, är och kunde vara.
#14
De stöder sig på omständigheten att ökningen av koldioxidhalten har gått 100 ggr fortare än under något tidigare tillfälle. Så klart går ökningen snabbt nu när vi släpper ut koldioxid. Men frågan är hur mycket skillnaden mellan 0,03 % koldioxid och 0,04 procent koldioxid har för inverkan.
#7 Magnus Cederlöf
Väldigt intressant modell ! Tycker den verkar robust.
En fundering är att T-offset skulle kunna bero på medelvärdet av instrålningen under ett år.
Tror inte att det skulle synas i din analys eftersom medelinstrålningen (under ett år) är konstant ?
Modellen ger ju en linjär klimatkänslighet. Kanske är linjärt trots allt ?
#7 Magnus Cederlöf
Underbar!
#21 Jonas
Ja T_offset beror på hur mycket medelvärdet av solinstrålningen är på ett år. Men det beror också på förhållandet mellan hav och land, topografin, havsströmmar mm.
Ja det ser ut som att det är approximativt linjärt mellan strålningseffekt och temperatur i det här fallet. Däremot är ju inte förhållandet mellan koldioxidhalt och strålningseffekt linjär.
Jo, men om T-offset beror av medelvärdet och medelvärdet ändras (p.g.a. högre forcing) så ska T-offset ändras i din beräkning av temperaturökningen.
Jag tror att du använder samma T-offset vid nuvarande instrålning som vid den förhöjda instrålningen.
Det borde vara svårt att räkna ut vilken T-offset man ska ha vid förhöjd forcing, eftersom anpassningen görs till data med konstant medelvärde. Det saknas ju data för en förhöjt medelvärde.
Antag att T-offset ändras med 3C när man höjer medlevärdet på forcingen med 5 W/m2 ?
Det är mycket möjligt att T-offset inte ändras så mycket, men vill bara peka på att det kan vara en osäkerhet i din modell.
Skulle vara mycket intressant om man på något sätt kan titta på hur T-offset påverkas av ändring i medelnivån.
Det påstås ju att forcingen har ökat med typ 1 W/m2 under de senaste 50 åren.
Om man gör analysen för 50 år gamla data (om de finns) och jämför med nutida data … ser man någon ändring av T-offset ?
I övrigt är jag imponerad av din modell.
När jag jämför med klimatteorier så tycker jag att de är matematiska mumbo-jumbon. Man lägger ut dimridåer genom att använda geggiga ekvationer.
Din modell går ju att förstå.
Jonas,
Jag tror att jag börjar förstå vad du menar. Som jag har räknat fram T_offset så har jag räknat på solinstrålningen (som är konstant) samt ett medelvärde av temperaturen för åren 1979 till 2013 (eftersom rapporten gjordes 2014). Om man även tar med nyare data så borde T_offset alltså också öka precis som du säger. Den här variabeln borde då helt enkelt följa marktemperaturen.
Men syftet med räkneövningen var inte att få fram en absolut temperatur utan att få fram vad en ändring i solinstrålningen ger för temperaturändring. Därför är T_offset av mindre betydelse.
Apropå räknenissar, varför inte räkna lite på klimatkänsligheten. Här kommer mina funderingar runt utstrålad energi i form av en enkel räkneövning:
Här kommer mina funderingar runt utstrålad energi i form av en enkel räkneövning:
Att räkna på jordklotet med en lag för svartkroppsstrålning är ju lite vanskligt. Jorden är ingen svart kropp och den är heller inte jämnvarm. Värden på albedo och emissivitet är osäkra. Dessutom är det ju en begränsad del av energin som lämnar jordytan i form av strålning.
Det går ju i alla fall att konstatera att vi inte har något linjärt samband. Utstrålningen beror på T⁴ och känsligheten blir beroende av lutningen på S-B-kurvan: F = εσT⁴ 1)
,där F är forcing i W/m², ε är emissiviteten, σ är Stefan-Boltzmanns konstant och T är temperaturen i Kelvin.
Lutningen får vi genom att derivera: dF/dT = 4εσT³ 2)
Här ser vi att temperaturändringen, dT, är omvänt proportionell mot temperaturen i kubik. En högre temperatur ger alltså en lägre känslighet.
Från IPCCs AR5 rapport får vi det logaritmiska sambandet mellan ändrad CO₂-halt och ändring i utstrålning: ΔF = k·log₂(C/C₀) 3)
,där k är en konstant som IPCC ger värdet 3,7 (egentligen 5,35 för naturlig logaritm, 5,35·ln2=3,7), C är aktuell eller framtida halt CO₂ i ppm medan C₀ är ett startvärde (t ex 280 eller 400 ppm).
Om klimatkänsligheten, S, definieras som temperaturökning vid en fördubblad CO₂-halt får vi sambandet: ΔT = S·log₂(C/C₀) 4)
Delar vi ekvation 3) med ekvation 4) får vi: ΔF/ ΔT = k/S
För små Δ kan vi skriva S = k / (dF/dT)
Ekvation 2) ger nu klimatkänsligheten: S = k/4εσT³
Låter vi k vara 3,7 (enligt IPCC) och emissiviteten vara 0,95 (min gissning) så får vi för T = -15°C att S = 1,0 och för T = +15°C att S = 0,7
I William Happers presentation ”How to Think about Climate Change” https://www.independent.org/issues/article.asp?id=13458 från 11/3-2021 anger han (i diagrammet med Schwarzschild-kurvan) ΔF till 3 vid en fördubblad CO₂ halt,
dvs k = 3. Vilket ger en något lägre känslighet än ovan.
Allt detta faller rimligen i och med att temperaturen inte är helt jämnt fördelat över jorden, men kan väl fungera som ett tankeexperiment. Eller om vi betraktar en begränsad yta av jorden med homogen temperatur, så att man vid varje given tidpunkt endast har en temperatur.
@Lasn
”Låter vi k vara 3,7 (enligt IPCC) och emissiviteten vara 0,95 (min gissning) så får vi för T = -15°C att S = 1,0 och för T = +15°C att S = 0,7”
Klimatkänsligheten definieras som ökningen i flux vid TOA för varje grad som jordytan ökar med.
TOA definieras som ”den effektiva utstrålningshöjden”, ungefär vid tropopausen. På den höjden stålar atmosfären ut ytterligare 3,3 W vid +1 grad.
Om utgående strålning ökar med 3,3 W när temperaturen vid ytan ökar med 1 grad så är det en klimatkänslighet med noll feedback. Om utgående strålning ökar med mer än 3,3 W så är det negativ feedback och om den ökar med mindre än 3,3 W så är det positiv feedback.
Så för en klimatkänslighet med noll feedback blir S = 1 och det finns ingen anledning att skilja mellan T(-15) och T(+15).
Erik,
Mitt resonemang bygger på att klimatkänsligheten definieras som temperaturökning vid en fördubbling av koldioxidhalten.
Vidare har jag använt de enkla sambanden som ges av Stefan-Boltzmanns ’T4-lag’ och det logaritmiska sambandet mellan CO2-halt och utstrålning, för att komma fram till ett enkelt uttryck klimatkänsligheten: S = k/4εσT³
Detta gör det tydligt att S ökar om k ökar (dvs stort ΔF för en given CO2-ökning). Liksom att S ökar vi en lägre emissivitet (ε < 1 t ex 0,95). Slutligen kommer vi till grunden för kommentaren, nämligen att S minskar om temperaturen ökar, som i räkneexemplet från 1,0 till 0,7. Dvs när temperaturen motsvarar jord utan atmosfär till dagens +15°C. Detta alltså i och med att lutningen på T4-kurvan ökar med ökat T, så att det går åt ett större ΔF för en viss ökning av T.
Här finns alltså inte med något av feedback, återkoppling, instrålning, konvektion, latent värme, osv. Bara kopplingen mellan CO2-halt, utstrålning och temperatur.
Lasn,
Allt är utmärkt utom en detalj. k (3,7 W) är forcingen, eller energiobalansen, vid tropopausen. Eller vid toppen av atmosfären när man tar hänsyn till nedkylningen i stratosfären.
k är inte forcingen vid jordytan. Om jordytan strålar ut ytterligare 3,7 W kommer det innebära att tropopausen strålar ut 2,3 W eftersom atmosfären absorberar strålning genom alla lager.
För att tillkommande värme vid jordytan ska återställa energiobalansen vid tropopausen måste jordytan stråla ut 6 W (390/240*3,7) motsvarande 1,1 K.