Här följer ett gästinlägg av meteorologen Anders Persson:
Gaspard-Gustave Coriolis, 1792-1843
Den här artikeln skrev jag ihop när jag trodde att min långa kommentar försvunnit i cyberrymden. Den ger en bättre sammanfattning och kommer med en del nya infallsvinklar. Jag har valt att refera till mina artiklar som jag skrev för SMHI 2007. Under de mer än 20 år jag forskat i ”corioliseffekten” har det blivit mycket skrivet bla. https://journals.ametsoc.org/doi/abs/10.1175/1520-0477%281998%29079%3C1373%3AHDWUTC%3E2.0.CO%3B2 , http://www.meteohistory.org/2005historyofmeteorology2/01persson.pdf http://www.meteohistory.org/2005historyofmeteorology2/01persson.pdf samt http://www.fysikersamfundet.se/wp-content/uploads/2004_3.pdf . Kanske är det bäst att starta med den sista, från Fysikaktuellt 2004.
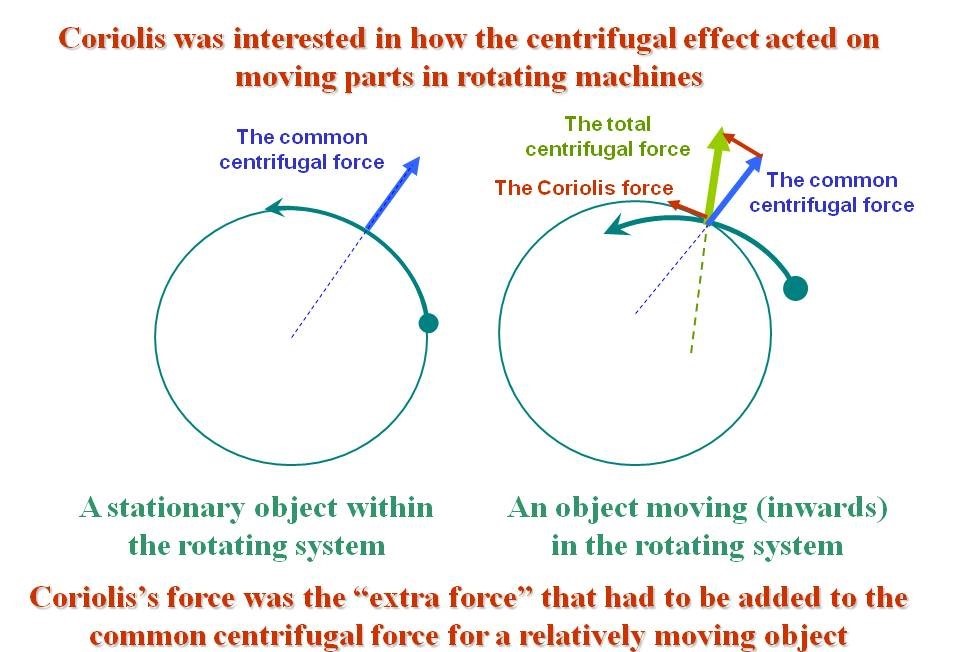
Det var först 1997, när jag läste Coriolis originaluppsats från 1835 som jag begrep ”hans” kraft. Coriolis var inte intresserad av jordens rotation utan rotationen hos maskiner. Som jag utförligt förklarar här är den förändringen av centrifugalkraften på ett föremål som också rör sig relativt rotationen Omega med hastigheten Vr.
Bildtext: Av pedagogiska skäl har jag i denna bild begått synden att blanda absoluta och relativa referenssystem. Å ena sidan ser vi rörelserna utifrån (grön tjock linje) år andra sidan ser vi krafter som bara uppträder när man följer med i rotationen (blå, ljusgröna och röda pilar). Corioliskraften är alltså skillnaden mellan den totala centrifugala kraften på en kropp som rör sig relativt rotationen och centrifugalkraften utan relativ rörelse.
Denna sk. ”corioliskraft” är alltså ingen egen, specifik kraft, utan bara en ”förlängning” av centrifugalkraften. Coriolis visade att den är 2Omega*Vr och vinkelrät mot Vr. Det visade sig att ”corioliskraften”, för de maskiner Coriolis var intresserad av, inte spelar så stor roll, centrigugalkraften dominerar. Icke desto mindre utgjorde hans upptäckt anledningen till att roterande rymdstationer, sådana som vi sett i Stanley Kubriks film ”2001” visade sig mycket svåra att använda. Detta utreds i slutet på min SMHI-artikel.
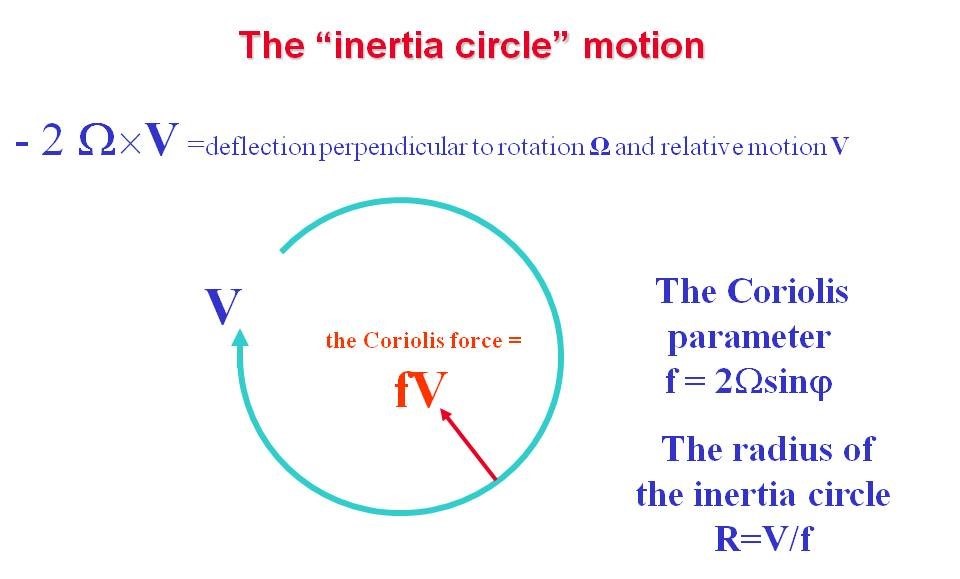
Detta att ”corioliskraften” är vinkelrät mot Vr innebär att den är en ”centralkraft”, dvs driver föremålet in i en cirkelrörelse med radien Vr/Omega. För ett föremål, friktionsfri ishockeypuck (inte rullande föremål) med hastigheten 1 m/s under en rotation på ett varv per sekund eller 2pi/sekund rör den sig i en cirkel, sk. ”tröghetscirkel”, med radien 1/2pi = 16 centimeter.
Bildtext: Ett föremål som friktionsfritt rör sig med hastigheten V i ett roterande system kommer att, pga corioliseffekten, följa en sk. ”tröghetscirkel”
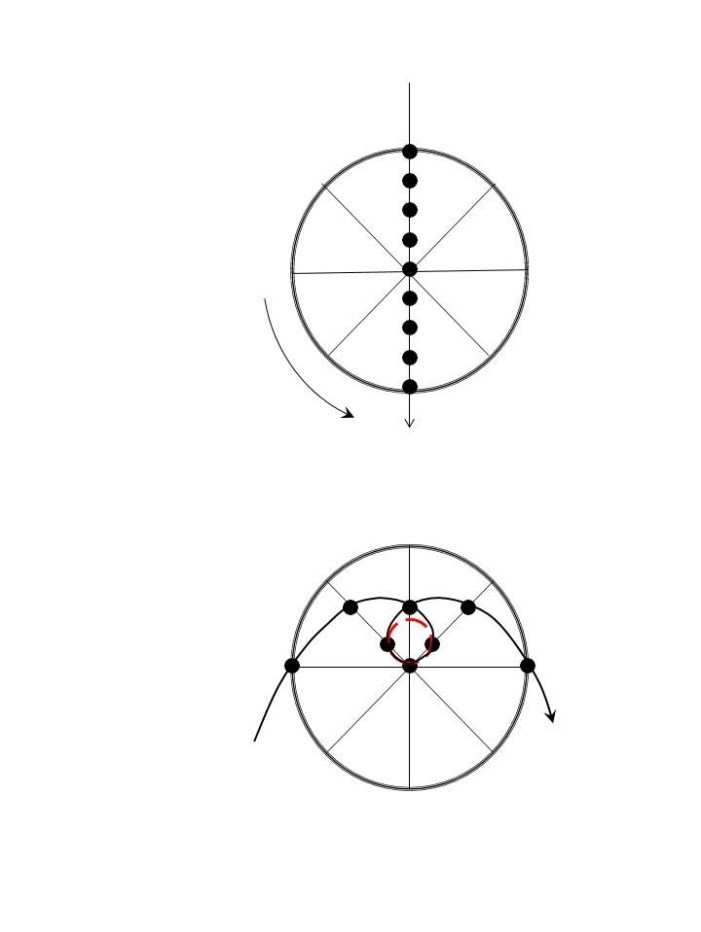
I en SMHI-artikel var jag kanske 2007 lite för kritisk emot experiment på karuseller. Sant är att det man oftast ser är en kombination av corioliskraftens avböjning och centrifugalkraftens utåtriktade acceleration. Om bara corioliskraften varit verksam skulle man ha sett föremålet drivet in i en cirkel.
Bildtext: Ett föremål rör sig friktionslöst över en moturs roterande karusell. Bilden ovan visar rörelsen sedd ”utifrån”, bilden nedan rörelsen sedd ”innifrån” dvs av en betraktare som följer med i rotationen. Vid och i närheten av rotationscentrum dominerar corioliskraften nästan helt varför rörelsen approximativt följer en sk. ”tröghetscirkel”.
Men detta går faktiskt att simulera på en karusell, nämligen om man håller sig nära rotationscentrum där centrifugalkraften är mycket svag. Detta beskriver jag i en artikel på en fransk sajt jag hänvisar till i den långa kommentaren.
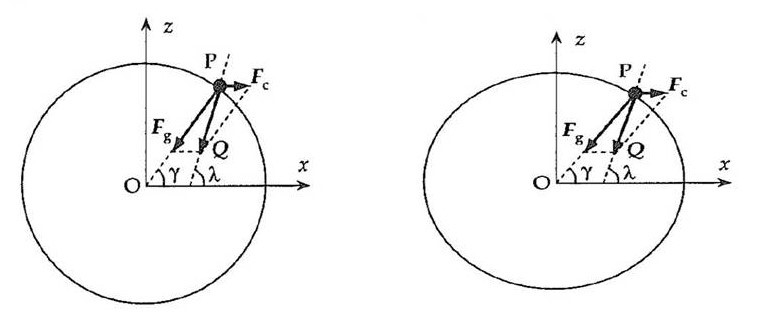
När vi kommer till roterande planeter är det lite vilseledande att tala om ”corioliskraften” inte bara därför att det egentligen bara rör sig om centrifugugalkraften, men också för att gravitationen, jordens dragningskraft, att skilja från tyngdkraften, som är en kombination av dragningskraften och centrifugalkraften. Inom parentes kan rapporteras att både svenska och utländska böcker i fysik ofta ger förbluffande vilseledande förklaringar av jordens tyngdkraft.
Bildtext: Till vänster en illustration ur Grahn och Janssons bok i fysik. Dragningskraften Fg pekar korrekt mot jordens centrum och centrifugalkraften Fc vinkelrätt mot jordaxeln. Men eftersom författarna inte ändrat jordens form kommer summan av de två, tyngdkraften, inte att följa en lodlinje, utan bildar en vinkel mot jordytan. Till höger: genom att ”stretcha” jpeg-bilden får jorden den icke-sfäriska form den har och som gör att tyngdkraften pekar vinkelrätt mot jordytan, ”rätt ner”.
Hur corioliseffekten beror på kombination av centrifugalkraft och dragningskraft (gravitation) utreddes på SMHI där kärnmeningen är:
”Springer vi västerut, mot jordens rotation, blir vår hastighet lägre (220-10=210 m/s) och vi påverkas av en något försvagad centrifugalkraft, som dock fortfarande är riktad söderut.
Försvagningen gör dock att balansen rubbas. Den norrut riktade dragningskraften får nu överhanden och driver oss på en minut 2 meter mot norr, sidledes och till höger, vinkelrätt mot vår rörelse.”
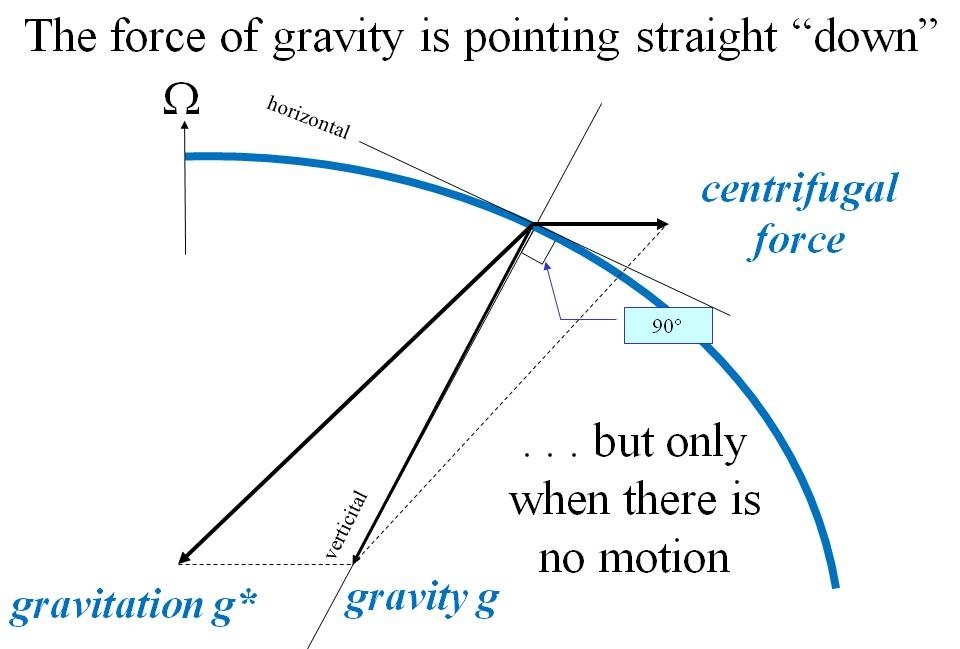
Bildtext: Krafterna som verkar på ett föremål i vila på den roterande jordens yta. Dragningskraft och centrifugalkraft samverkar i en tyngdkraft som är riktad ”rakt ner”.
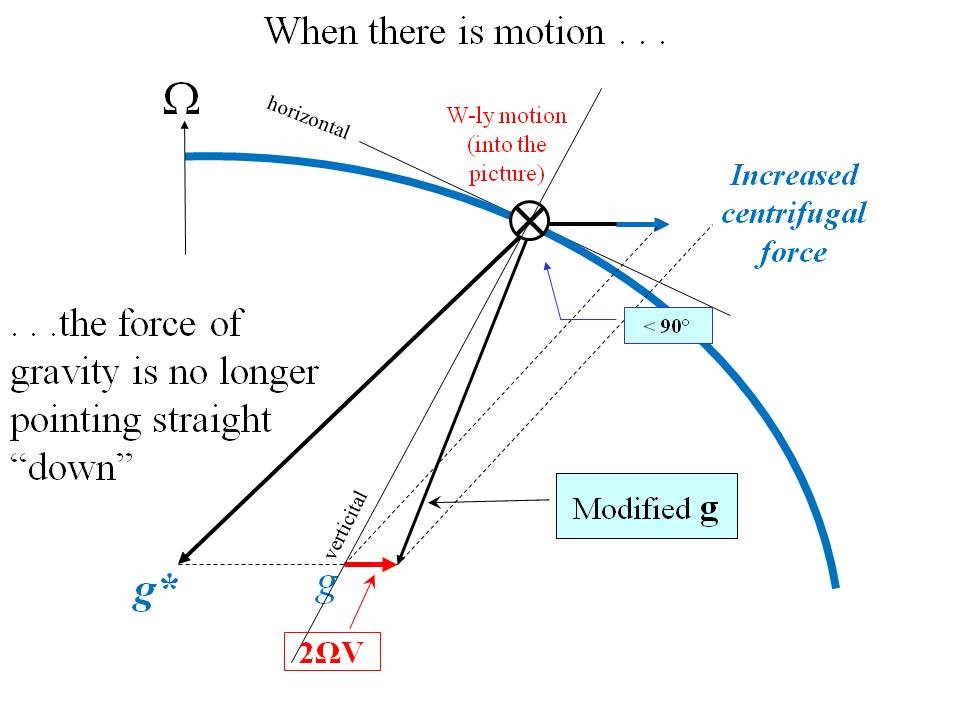
Bildtext: För rörelse österut, i samma riktning som jordrotationen, ökar centrifugalkraften – en fiktiv kraft – och ger en acceleration söderut, till höger om den relativa rörelsen.
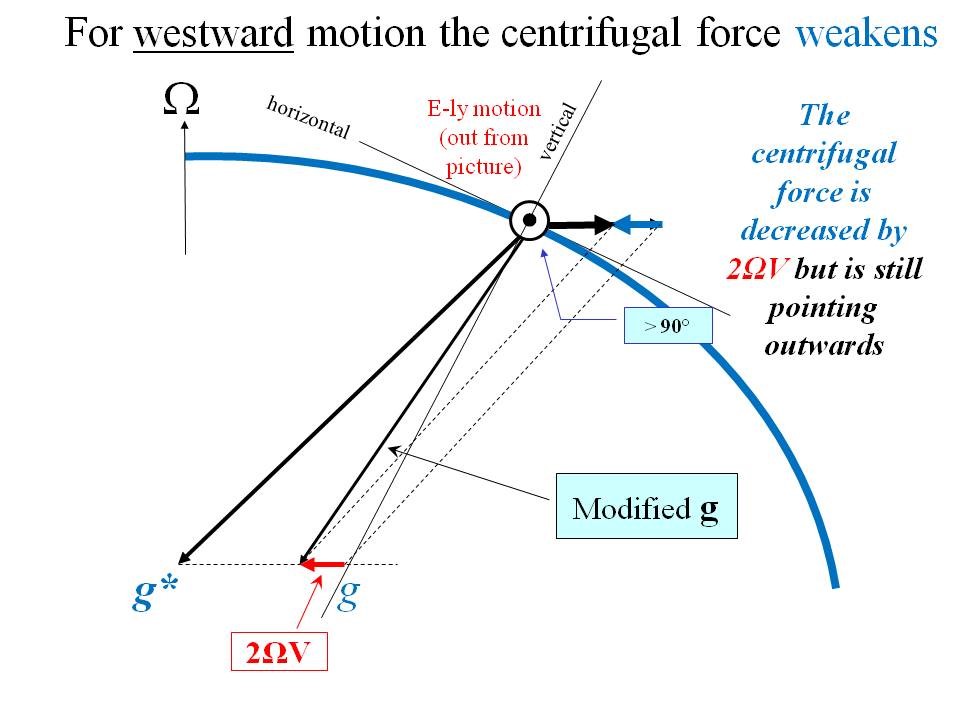
Bildtext: Rör sig föremålet västerut, mot jordrotationen, försvagas centrifugalkraften och dragningskraften – en icke-fiktif kraft – får ”överhand” och accelererar föremålet mot jordaxeln, norrut och återigen till höger om den relativa rörelsen. Nu liksom i det före fallet tillskriver vi denna avlänknng åt höger en ”corioliskraft”.
Att det för västgående rörelse är gravitationen som accelererar kroppen norrut, återigen till höger om rörelsen, påpekades för första gången 1993 av den ansedde amerikanska meteorologiprofessorn Dale Durran. Jag har vidareutvecklat och fördjupat analysen i https://rmets.onlinelibrary.wiley.com/doi/abs/10.1002/qj.2477 som det tog Royal Meteorological Society mer än två år att godkänna. Detta berodde på att Durrans och min tolkning bryter mot 150 års ”accepterad visdom” att ”corioliseffekten”, till skillnad från ”corioliskraften” är en ren tröghetsrörelse. Detta kan vara en uppmuntran till alla ”skeptiker” som inte vill acceptera att vetenskapsmän är 100% eniga och att allt som man trott länge därför nödvändigtvis är sant.
Relativ rörelse över en roterande planet följer också cirkelrörelser, dock inte 100% perfekta eftersom ”corioliskraften” beror av (sinus av) latituden. Detta visas och utreds i de länkar som avslutade min långa kommentar, och passar kanske att avsluta denna gästartikel https://www.smhi.se/polopoly_fs/1.5479.1490012459!/image/yllemossan_figur2.PNG_gen/derivatives/Original_1256px/image/yllemossan_figur2.PNG i SMHI-kapitlet https://www.smhi.se/kunskapsbanken/meteorologi/jordrotationens-yllemosse-effekt-1.5474
Bildtext: På en roterande planet, där corioliseffekten är en funktion av latituden, kommer corioliseffekten driva in rörelsen i en cirkulär bana, som dock öppnar sig västerut.
Mot allt ”sunt förnuft” gör jordrotationen det inte bara svårt för rörliga föremål att förflytta sig några längre sträckor, låsta som de är i ”tröghetscirkelrörelser”, den förflyttar också föremålet sakta västerut.
Andra meteorologiska och oceanografiska tolkningar hittar ni här.
Anders Persson
”Våren 1968 biträdande meteorolog vid väderprognosavdelningen, ”Vädertjänsten”. 1973 befordran till prognosmeteorolog tjänstgöring som semestervikarie vid Göteborgs och Malmö flygplatser 1976, 1977 och 1989-90. Var 1972 med att starta en svensk meteorologisk tidskrift Polarfront. 1993–2013 periodvis knuten till European Centre for Medium Range Weather Forecasts i England. Åren 1991–2001 fast anställd vetenskapsman. 2008–2010 anställning vid den den brittiska vädertjänsten Meteorological Office i Exeter.” Ur https://sv.wikipedia.org/wiki/Anders_Persson_(meteorolog)

Professor emeritus i filosofi. Forskningsinriktning är vetenskapsteori, teknikfilosofi och politisk filosofi. Huvudredaktör för Klimatupplysningen.










Jag fattar vad Corioliskraften är. Trots en så detaljerad förklaring att det är lätt att förlora sig i detaljer. Att jorden är stor och att det är långt till solen gör ju att centrifugalkrafter inte märks lika tydligt som om man sitter i en karusell.
Tack Anders,
för en utmärkt redogörelse.
En sak du inte nämner är att eftersom den polära rörelsen drivs av den ”verkliga kraften”, d.v.s. gravitationen så ökar hastigheten vid nordgående rörelse (samtidigt som gravitationspotentialen minskar), så att hastigheten är som högst när ”det friktionslöst sig rörande föremålet” är som närmast polen.
När jag läser min långa artikel med alla dess länkar slår det mig att kanske inte alla orkar gå igenom den i alla dess detaljer. Så kanske kan följande 5-punktssammanfattning vara tillfyllest för dem som har bråttom:
1. På en karusell pekar rotationsaxel vertikalt mot ”karusellplanet” och all rörelse (V m/s) sker därför vinkelrät emot rotationsaxeln. Också centrifugalkraften och dess avknoppning, ”coriolskraften”, verkar endast vinkelrät emot rotationsaxeln. Enda sättet att skilja dem åt, att lyfta fram just ”corioliskraften”, är att uppehålla sig så nära rotationscentrum att centrifugalkraften är mycket mindre än ”corioliskraften”.
2. På en roterande planet besväras vi, vid och mycket nära polerna, av samma skäl, inte av någon centrifugalkraft, trots att rörelsen sker på ett ”karusellplan” som är så gott som vinkelrät emot rotationsaxeln (rotationens storlek=Omega radianer/sekund).
3. På alla andra latituder kan V delas upp i en komponent som är parallell med detta ”karusellplan”, vilken är V multiplicerad med sinus för latituden, och en komponent som är parallell med rotationsaxeln och därför inte påverkas alls. Därav formeln 2Omega*sinus(latitud)*V för corioliskraften på en roterande planet.
4. Med ökande avstånd från polerna ökar centrifugalkraften pga jordens rotation och man skulle kunna befara att den, återigen, kommer att kraftigt överskugga ”corioliskraften”. Men, som jag visar i huvudartikeln, jordens icke-sfäriska form, som den fått pga rotationen, gör att en komponent av dragningskraften (gravitationen) perfekt balanserar, släcker bort, centrifugalkraften.
5. Samma resonemang kan tillämpas för det fall då man har en karusell, som man i Sten Kaijsers anda, deformerar till en parabol. Men här är det en komponent av tyngdkraften (på engelska ”gravity”) som släcker ut centrifugalkraften.
Svar till #2 Arne Nilsson: Att vi inte känner av centrifugalkraften pga jordens rotation har inget med solen och dess avstånd att göra utan beror på jordens form. En trevlig kuggfråga, som även fått professorer på fall, är: -Varför kan vi spela curling i Uppsala? Centrifugalaccelerationen är här ca 15 mm/sekund**2 och skulle, vid spel i öst-väst, ge en av avdrft på några meter.
Svar till #3 Sten Kaijser: Tack för uppskattningen! Du har rätt vad avser föremålets absoluta hastighet, dvs sedd ”utifrån”. Men befinner vi oss på jorden så kan vi ”innifrån” inte se någon ökning av hastigheten. Det är heller inte att vänta eftersom sidoacceleration pga corioliseffekten alltid är vinkelrät emot den relativa hastigheten.
Tack Anders Persson för en utmärkt redogörelse. Nu får jag inte texten i bild 3 att fungera. Börjar vi med texten i första bilden, som jag tycker är OK, står det,
”å andra sidan ser vi krafter som bara uppträder när man följer med i rotationen.”
I tredje bildtexten står det,
”Ett föremål rör sig friktionslöst över en moturs roterande karusell.”
Det innebär att föremålet INTE följer med i rotationen, de bara rör sig oberoende av varandra. Då uppträder inte coriolis vilket bevisas av att föremålets bana är rak, banan påverkas ej av någon kraft. Hur observatören rör sig saknar betydelse. Om man monterar kameran i en drönare som åker litet hur som helst kan man få en ganska lustig kurva som helt saknar knytning till coriolis.
”dvs av en betraktare som följer med i rotationen.”
Den texten är nonsens och det är inte så det står i texten till bild 1. Det är föremålet som skall följa med i rotationen. Vilka piruetter betraktaren gör saknar betydelse.
Svar till #5 Lars Cornell: Corioliskraften är ingen ”riktig” kraft, bara en ”skenkraft” som bara ger sig till känna när man deltager i rotationen. Så det är helt konsistent att när man ”utifrån” betraktar ett föremål som rör sig friktionsfritt över en snurrande plattform, så ser man att den rör sig rakt. Men ”innifrån”, då man är ombord på plattformen, som vi är ombord på den snurrande en snurrande planet, så observerar vi hur rörelsen viker av pga corioliseffekten. Skillnaden mellan att vara ombord på karusellen och ombord på en snurrande planet är att i det förra fallet påverkas det vi ser av den likaledes fiktiva, centrifugala skenkraften, medan centrifugalkraften på en snurrande planet är ”nersläckt” av dragningskraaften-gravitationen, i Sten Kaijsers snurrande parabol av tyngdkraften.
Härligt!
Det här är en bra blog där man ständigt lär dig.
I en tidigare debatt var det tal om nödvändigheten att inkludera friktionen eftersom det sades vara enda sättet som föremålet skulle kunna ”veta” att det befann sig i en roterande omgiving.
Icke.
Tänk er att ishockypucken, som rör sig friktionsfritt över den roterande karusellen, bär en liten groda. Tittar grodan ”utåt”, mot omgivningens träd, hus och kanske människor, har det ingen känsla av att det befinner sig på en roterande karusell – det bär ju rakt framåt.
Men tittar grodan ”neråt”, mot det lite smutsiga karusellgolvet, ser den att pucken rör sig relativt denna. Det skulle grodan också se om den från början befunne sig på karusellens golv. Pucken skulle komma svischande förbi.
Annat är det på en roterande planet. Ishockypucken (med grodan) rör sig fortfarande friktionsfritt över planetens yta. Tittar grodan ”neråt” ser den att pucken rör sig i en böjd bana, approximativt i en (tröghets)cirkelrörelse. Tittar den ”uppåt” har den inte många referenspunkter mer än stjärnorna och dessa kommer inte att ge fog för påståendet att pucken rör sig i en rät linje i förhållande till dem.
Nu har grodan lyckligtvis en lite mobiltelefon så den ringer till en grodkompis i en satellit högt upp. Den ser sin kompis snurra runt med planeten, samtidigt som den rör sig mellan två latituder, vilka begränsar (tröghets)cirkelrörelsen. Den utomstående grodan ser alltså ingen rät linje utan en slags cykloidformad bana, något i stil med den blå-streckade kurva ni kan se på bilden en bit ner på denna sida https://thatsmaths.com/2015/09/17/the-ubiquitous-cycloid/
Så det är fundamentala skillnader mellan corioliseffekten på en roterande karusell och på ytan av en roterande planet.
#6 Anders. NEJ !
Coriolis är liksom centripetalkraften en riktig kraft, den går att mäta med tex en fjädervåg i ”snöret”. Coriolis är en förändrad centripetalkraft på grund av förändrad hastighet som får föremål att ändra bana men ej hastighet.
”när man deltager i rotationen”, vilken ’man’?
Gör följande. Låt karusellen stå still och bara fotografen snurrar. Vad händer då?
Skall jag hjälpa dig på traven med svaret? Det händer samma sak om föremålet rör sig friktionslöst !
.
#8 Ja, det är så fundamentala skillnader att corioliskraften (förutsatt att friktion saknas) är noll på en karusell antingen karusellen roterar eller inte.
Om karusellgolvet är smutsigt, grodan är grön eller svart och har ett blått och ett gult öga och om det är söndag eller tisdag och vad drottningen heter saknar också betydelse för hur den friktionsfria pucken rör sig.
Hmm, lite intressant att se hur mycket felaktiga beskrivningar det finns om corioliseffekten.
Dessa kommer upp först om man googlar:
National Geographics: beskriver Hadleys förståelse
https://www.nationalgeographic.org/encyclopedia/coriolis-effect/
Encyclopedia Britannica: hmm, helt förvirrad?
https://www.britannica.com/science/Coriolis-force/media/1/137646/169053
NOAA: Hadley igen?
https://scijinks.gov/coriolis/
PBS Nova : karusellen med brist på framförhållning
https://www.pbs.org/video/what-coriolis-effect-ayondr/
North Carolina Climate Office: Hadley igen
https://climate.ncsu.edu/edu/Coriolis
Vad säger det oss om hur mycket felaktiga beskrivningar det finns därute som även stora institutioner sväljer med hull och hår?
Nu Anders Persson och Sten Kaijser kom jag på en bra liknelse. Tänk dig att du åker tåg över prärien. Där springer en häst vid järnvägen. En passagerare tar upp sin filmkamera och fotograferar hästen. När han kommer hem upptäcker han att hästen står stilla. På varenda filmruta är hästen på samman ställe. När han tittade ut kunde han svära på att hästen sprang vid tåget, men filmen han tog bevisar att hästen stod stilla. Märkligt eller hur. Kan det vara den mystiska coriolis som spökar?
Svar till #9 av Lars Cornell: Vi är vana vid att en X-kraft skapar en X-accleration. Så den f i k t i v a corioliskraften borde alstra en coriolisacceleration riktad åt samma håll. För att komplicera saken har nu Människan definierat en sk ”coriolisacceleration” som, genererad av en r i k t i g kraft, är motriktad corioliskraften. Alltså ”coriolisaccleration” motverkar och balanserar den acceleration som genereras av corioliskraften.
I Naturen sker detta t.ex. av horisontella tryckskillnader i hav och atmosfär (tryckgradientkraften). Det är därför vi ser vinden blåsa ungefär mitt emellan hög- och lågtryck (ungefär parallellt med isobarerna): corioliskraftens högerriktade acclerationen balanseras av tryckgradientens vänsterriktade.
Vår oenighet beror på att du diskuterar coriolisacclerationen i tron att den är genererad av corioliskraften. Det borde vara så, men Människan har i sin outgrundliga visdom definierat det tvärtom – för att ytterligare förvilla sig själv!
Svar till Johan M:s kommenar #11: Det verkligt paradoxala är att vetenskapsmännen vetat i mer än 150 år att Hadley’s förklaring är fel. Men de saluför den ändå därför att den är så lätt att använda som förklaring. En kollega till mig, professorn John Knox https://en.wikipedia.org/wiki/John_Knox_(meteorologist) som till 100% har samma uppfattning som jag om Corioliseffekten är, har han sagt mig, förbjuden av sitt bokförlag att presentera den riktiga förklaringen, ty då skulle inte lärarna köpa hans bok.
Jag har sedan 1998 föreläst om corioliseffekten på en massa, massa universitet och högskolor på alla kontinenterna (utom Antarktis). Ingen har sagt att jag har fel, men ingen tar rättning, utan fortsätter som vanligt.
Nej, det var fel. I ett land har lyckats vinna en 100% seger, nämligen Nya Zeeland!!!
Lars Cornell #12: Skämtar du med oss? Det du beskriver är skillnaden mellan absolut och relativ l i n j ä r rörelse, som Galielo utredde (och förmodligen flera före honom).
På 80-talet tävlade jag i varmluftsballong. Jag kommer ihåg att corioliskraften diskuterades bland piloterna och om ballongen kunde påverkas av denna kraft men jag fick aldrig klarhet i frågan.
Fråga: Påverkas ballongen av corioliskraften?
#15 Linjär rörelse är också vad figur 3 visar, både den övre och den undre figuren. Det är en linjär rörelse eftersom inga krafter påverkar föremålet. Men där kallas det felaktigt coriolis.
Men i fotografens kamera ser det annorlunda ut eftersom fotografen rör sig. Det gäller både figur tre och hästen på prärien.
Jag upprepar för femtioelfte gången, coriolis har ingenting med hur kameran rör sig att skaffa.
#14 Anders Persson
#16 Snurrigt, det här (pun intended!). Hela grejen kretsar (igen!) kring just det där med vad som är linjärt. Relativt ett orörligt referenssystem är rörelsen linjär, men inte relativt det roterande klotet. Allt beror på var betraktaren befinner sig. Lätt som en plätt!
#18 Mattias. Jag gillar det du skriver, men du når inte riktigt ända fram.
Puckens friktionsfria rörelse över karusellen, antingen karusellen snurrar eller är stilla, är lika linjär som hästens galopp över prärien. #15 i
https://www.klimatupplysningen.se/2019/08/13/annu-mera-coriolis/
Om en rörelse är linjär är det ett starkt bevis för att föremålet inte utsätts för någon kraft.
När det gäller det roterande jordklotet måste föremålet följa jordytans krökning (en krökning som karusellen saknar). För att det skall kunna ske behövs krafter, en av dessa krafter är coriolis. Därför blir inte sådan rörelse linjär.
Ytterligare en skillnad, en luftmassa följer med i jordens rotation, det gör inte pucken som friktionsfritt rör sig helt frikopplat från karusellens rörelse.
Lars Cornell #19: Du måste, för att komma till reds med dina undringar, och få mig att förstå vad du menar, skilja på absolut rörelse och relativ rörelse, liksom mellan verkliga krafter och fiktiva. Sedan är det viktigt att göra klart om det som sätter igång rörelsen över jordytan är en impuls eller en (verklig) kraft.
Tydligen blev det klarlagt att coriolis effekten är en fiktiv kraft. Jag tycker Mattias G har rätt i att det beror mycket på var betraktaren befinner sig.
I karusellexemplet kan jag inte se att det blir en cirkelrörelse om inte pucken är så långsam att karusellen hinner ta ett varv eller mera innan pucken hunnit från centrum till utanför periferin. Då ritar puckens skugga en cirkelaktig bild på karusellens golv men pucken själv går rakt. Detta till skillnad från dom hastighetsvektorer den hade haft ifall starten skett från en roterande plattform.
En fråga till författaren. Bildtexten i bild 5 ”The force of gravity is pointing straight down….but only when there is no motion”. Kanske det är bildligt talat med tanke på citationsteknen men jag undrar hur man tänker sig att gravitationens riktning avviker från gravitationscentrum?
#20 A.P. Jag har förmåga att kunna skilja på sådana saker.
Coriolis sysslade med absoluta rörelser och absoluta krafter som fick maskiner att gå sönder. Jag sysslar med det verkliga medan det skenbara och synvillor gör mig likgiltig.
Här har jag nått gränsen för min pedagogiska förmåga.
Guy #21: Jag skulle nog säga att ”coriolis k r a f t e n” är en fiktiv kraft. ”Coriolis e f f e k t e n” däremot består både av corioliskraften och jordens dragningskraft, och den är inte fiktiv.
Oklart formulerat av mig. Du har rätt i att det blir en cirkelrörelse först om pucken rör sig långsamt. Jag borde ha skrivit något i stil med ”en cirkelaktig krökning”. Uttrycket för ”tröghetscirkelns” radie kan ju också användas för att bestämma krökningsradien för en krökt bana.
Med ”straight down”, dvs ”rakt ner” menar jag vad en person upplever på jordytan, dvs en rörelse vinkelrät mot jordytan eller parallellt med en lodlinje. Bara vid ekvatorn och polerna pekar den också mot jordens medelpunkt, eller ”gravitationscentrum”, som du kallar den.
Ja, ska man vara petig så pekar inte heller dragningskraften e x a k t mot jordens medelpunkt (bortsett från vid ekvatorn och polerna) eftersom jorden inte är en perfekt sfär. Men den avvikelsen är så liten jämfört med avvikelsen från lodlinjen, att den brukar försummas.
Guy #21. Ja det är bra. Vi fokuserar så mycket på verkliga och ännu mer fiktiva och skenbara rörelser att själva kraften glöms bort. Med ordet ’fiktiv’ inbillar man andra och sig själv att den nog inte riktigt finns i verkligheten. Det är i så fall en mycket felaktig beskrivning.
Corioliskraften är en stark kraft (liten energi men stark kraft) som ibland får maskiner att gå sönder och enorma luftmassor att röra på sig. Det var sådan ingenjörskonst som sysselsatte coriolis.
Hm, ibland är det måhända enklare att avstå från att förstå…. (ungefär som att jag avstod från att försöka förstå hur det ’går till’ i Japan den gången för 20ys sen jag var där på några månader..)
och istället bara använda ekvationerna.
Fast jag kommer ihåg hur jag använde ett par vektoralgebraiska uttryck för att få rätt på en del problem.
*frilägg och sätt ut krafter* minns jag väl
Lars Cornell #25. Du skriver: ”Corioliskraften är en stark kraft (liten energi men stark kraft) som ibland får maskiner att gå sönder och enorma luftmassor att röra på sig. ” Detta är rent ut sagt abakadraba. Eftersom corioliskraften är vinkelrät mot rörelsen kan den inte, inte ens om den var en riktig kraft, alstra ett uns energi, hur stark den sedan än månde vara.
Argus #26: Jag fick en fråga om inte förvirringen kring corioliseffekten har haft en förvirrande verkan på meteoologin. Jo, högsta grad – och i 150 år. Det kan finnas anledning att återkomma till detta, men låt mig bara kort säga att en del meteorologer har löst problemet på ”ditt” sätt, dvs bara låtit härleda ekvationerna, struntat i vad de betyder och sedan stoppat in dem i en dator, som gör de korrekta slutledningarna. Andra lämnar dynamiken och går över i kinematiken, där kraftbegreppet och därmed kausaliteten saknas helt. Mycken förvirring skapas ändå därför att de inte inser att de är inom kinematiken och söker dra slutsatser som vore det dynamik.
#26 Orden ”liten energi” ångrar jag. Det jag hade i tankarna var all den energi som finns i luftsnurrorna, havens strömmar och hur den påverkas.
Las C #26
”Corioliskraften är en stark kraft (liten energi men stark kraft) som ibland får maskiner att gå sönder och enorma luftmassor att röra på sig. Det var sådan ingenjörskonst som sysselsatte coriolis.”
Av ren nyfikenhet och i brist på tillräcklig teknisk kunskap vill jag fråga. En roterande maskin (maskin med roterande delar) vill inte ändra riktning frivilligt. Tvingas den slits axlar och lager. En maskin som står stationärt på jorden har inte samma problem eller har den problem med att följa med i jordens rotation. Är det skillnad om maskinens rotationsriktning är i samma riktning som jordens rotation eller vinkelrätt emot den?
Kanske helt dum fråga, men jag undrar om det är så och ifall det är mätbart?
#29 Guy Det är svåra frågor du kommer med.
Maskiner har nog inga problem med jordens rotation eftersom den är så långsam.
– Det tydliga exemplet är en rymdstation i toroidform som roterar för att simulera tyngdkraft. Där blir corioliskrafterna stora som beskrevs i den här bloggen vid något tillfälle. Man måste ha den roterande delens axel parallell med toroidaxeln för att undvika problem. Människor kan enkelt stå upp i en sådan toroid, men att röra sig medför problem.
https://en.wikipedia.org/wiki/Toroid
– Piloter vet att propellerflygplan har en tendens att tippa över åt ena hållet vid stark sväng. Jag är gammal pilot och har tydligt upplevt det och det kan föranleda spinn.
– En helikopter som svänger påverkas av coriolis. Man måste vrida styrmekanismen rätt mycket för att kompensera krafterna.
– Det finns karuseller med små karuseller på den stora karusellplattan. De måste vara mycket starkt infogade för att inte brytas sönder av corioliskraften. Det har hänt olyckor där den lilla karusellen lossnat.
– Cavitation i vattenturbiner har varit ett rätt stort problem. Det problemet beror till viss del på coriolis.
– Om en vattenslang lossnar och vattnet sprutar fritt börjar slangen svänga. Jag tror att det beror på coriolis.
– För att mäta flödet av vätskor kan man använda coriolis som får vätskan att svänga.
Har du funderat på skillnaden mellan gyroeffekten och corioliseffekten?
Mitt kunskapsområde är inte maskiner utan elektronik. Andra har kanske bättre exempel.
#30 Lars C
Tack för ditt svar.
Jag början i slutändan. Jag tänkte faktiskt sätta med gyroeffekten. Det är fråga om samma ovilja att ändra riktning.
-Vattenslangen ser jag ingen coriolis effekt i. Det utsprutande vattnet har en ”jet-effekt” på slangen.
– Kavitation i en propeller känner jag till, men i en aktersnurra beror det främst på en för häftig sväng där vattentillförseln inte hinner med propellerns rotation. Eller propeller hamnar för nära vattenytan.
– Karusellen kan jag inte uttala mej om, men kan tänkas bryts den mindre karusellen på grund av kraftskillnaden mellan centrifugal och centripetalkraften i den stora karusellen.
-Helikopter?
-Jag har inte upplevt samma som du i enmotorigt propellerplan. Tippning endast vid så långsam flygning att den övergår i stall. Då tippar vissa plan över eller sänker ena vingen. Troligen till följd av propellerströmmen.
Guy #29: Den maskin du beskriver fungerar i praktiken som ett gyroskop, som ”vill” behålla sin orientering tack vare rotationen. Därför används gyroskop för navigering i luft- och rymdfart, liksom för att stabilisera fartyg https://sv.wikipedia.org/wiki/Gyroskop
Gyroskopets mekanism är intimt förknippat med corioliskraften, vilket anas eftersom den ”injicerar” en slags tröghet eller motstånd mot rörelseförändringar, jämförbart med den ”seghet” som corioliseffekten injicerar i roterande gaser och vätskor. Bland flödesdynamiker i Cambridge talar man om ”Coriolisstiffness”.
Att Leon Foucault, mannen bakom ”pendeln”, vidareutvecklade gyroskopidén och gav den dess namn, skulle ha misslyckats med att med den visa jordens rotation, som påstås i svenska Wikipediaartikeln, har jag svårt att förstå. Det finner inget stöd vare sig i engelska eller franska artiklarna.
Lars C #30: I de flesta av de exempel du nämner är det centrifugalkraften som ställer till trassel. Corioliskraften uppträder inte bara när något ”gör en sväng” utan om detta ”något” också samtidigt rör sig relativt ”svängen”. I de allra flesta fall, utom vid eller nära rotationscentrum, är centrifugalkraften alltid mycket kraftigare än corioliskraften.
Antag att någon rör sig med hastigheten 1 m/s i en buss som tar en kurva. Rör sig bussen med moderata 10 m/s och krökningsradien i kurvan är stor, säg 50 meter, är centrifugalkraften fem gånger kraftigare än corioliskraften, kör bussen med 20 m/s och krökningsradien är 10 meter, är centrifugalkraften tio gånger kraftigare – om bussen alls kan hålla sig kvar på vägbanan!
Förhållandet mellan centrifugalkraft och corioliskraft = U/2V där U är bussens hastighet och V passagerarens relativa hastighet inne i bussen. Lägg märke till att krökningsradien inte spelar någon roll.
Tack för svaren. Stundom undrar jag om coriolis -benämningen används på fenomen där den kanske inte hör hemma. Som att sätta namn på en företeelse endast för att det låter bättre eller att man inte vet.
Coriolisstiffness låter märkligt. Flödesdynamik är, vad jag förstår, synnerligen komplicerad. Speciellt när den lätt övergår i kaos. Aerodynamiken, antar jag, hör dit och den har lärts ut galet hur länge som helst.
Förvirringen inom den meteorologiska samfälligheten vad gäller corioliseffekten framgår av den här BBC dokumantären https://www.youtube.com/watch?v=Wda7azMvabE som inleds med att tre framstående brittiska meteorologer får frågan: -Vad är corioliseffekten?
Det slutar med att de hänvisar till en av världens främsta dynamiker, min gode vän professorn Brian Hoskins, som genomför en demonstration med en parabol, liknande den som Sten Kaijser nämnde tidigare.
En kanske bättre demonstration görs vid University of Washington i Seattle under ledning av min likaledes gode vän, professorn Dale Durran
https://www.youtube.com/watch?v=OT7O_1MdFKc
Kanske är programledaren Jeff Renner lite för kritisk emot demonstrationer på en platt karusell: uppehåller sig bollen nära rotationscentrum dominerar corioliskraften över centrifugalkraften. Det är dock olämpligt att använda en boll eftersom dess impulsmoment injicerar en viss tröghet i dess rörelse pga lagen om bevarandet av impulsmomentet.
#31. Jetkraften uppstår vid mynningen. Coriolis uppstår inuti slangen när den ligger i en båge och vätskan flödar.
En båtpropeller arbetar i stillastående vatten. I vissa sorters turbiner roterar vattnet.
Karusellen ät ett typexempel som ligger mycket nära hur jordytan röra sig tex i Uppsala.
https://www.aftonbladet.se/nyheter/a/m6P1eg/karusell-kollapsade-15-barn-skadade
Det var huvudaxeln som gick av och den är inte utsatt för några centrifugalkrafter, endast för coriolis (eller gyro) som man tydligen försummat att beräkna vid konstruktionen.
Motorns vridmoment kan kanske ha viss inverkan. Men det borde kompenseras när propellerströmmen når vingarna.
#32. Jag tror att du tänker och räknar helt rätt. Men att centrifugalkraften är större än coriolis förtar inte att den senare effekten är verksam. Vi kan kompensera centrifugalkraften genom att personen som står i bussen trycker ryggen mot en stolpe i bussen, fast det är svårt att ta ett steg framåt då.
Eller att personen följer med i centrifugalkraften. Står han på bussens högra sida och bussen svänger höger kommer han att falla vänster (= bakåt) i bussen om han har fötterna på golvet. Alternativt kommer han att driva i väg bakåt i bussen om friktion mot bussgolvet saknas. En låda på golvet skulle driva iväg bakåt i bussen samtidigt som den påverkas av centrifugalkraften. Det blir bakåt oavsett om bussen svänger höger eller vänster.
Guy #33: Att tala om ”coriolisstiffness” som man gör bland flödesdynamiker i Cambridge är inte alls ”märkligt”, det borde man göra över hela världen. Ty till det ”märkliga” med corioliseffekten är just detta, att de gör roterande gaser och vätskor ”segare”.
En pingpongboll poppar upp långsammare i en vätska som roterar än i en stillastående vätska
https://commons.wikimedia.org/wiki/File:Taylor_column_rising_ball.png
eftersom den undanträngda vätskan ”vill” återvända och den intrömmande vätskan ”vill” återvända, i båda fallen genom ”tröghetscirklar”. Om detta och annat om de sk. ”Taylor kolumnerna” kan ni läsa i min artikel från juni 2001 http://rus.ums.rshu.ru/file1538
Lars C: #35: Återigen vet jag inte om du narras med oss. Som jag påpekat flera gånger, och som framgår av ekvationen för centrifugalkraften, är den noll i rotationscentrum, där karusellens axel befann sig. Eftersom det det fanns någon relativ rörelse fanns det inte heller några corioliseffekter.
Centrifugalkrafter fanns det däremot längre ut från rotationscentrum och eftersom centrifugalkraften också beror på massan kan det uppstå obalanser om massan är ojämnt fördelad på karusellen.
Tack för länkarna Anders, de visar ju ”in real life” det som mitt tanke-experiment handlade om.
Tanken att efterlikna jordens tillplattning med en roterande parabolisk skål och därmed balansera centrifugalkraften med en gravitationskraft. Det var ju också roligt att se att Coriolis-effekten sitter i betraktarens öga. Det skulle nämligen ha varit rubriken på det inlägg jag, tack vare ditt ingripande slapp skriva.
#37 Anders. Har du aldrig åkt riktig karusell? Se länken i #35?
Centrifugalkraften är noll i rotationcentrum, det är vi ense om och det skrev jag också.
Om du tar en ’platt’ barn-karusell och snurrar den. Därefter monterar du den på en arm som du höjer litet. Därefter vinklar du alltsammans ca 30 grader mot jordytan. Slutligen snurrar du runt hela härligheten med kanske ett varv på två eller fem minuter. Då får du en snurrande karusell (”Föremål”) som befinner sig i ett roterande system helt enligt coriolis förutsättningar.
En sådan anordning liknar mycket ett lågtryck över Uppsala som snurrar runt med jorden ett varv på 24 timmar.
Axeln blir utsatt för kraftiga skjuvkrafter (”bryta-av-krafter”) på grund av coriolis.
De krafterna sitter inte i betraktarens öga.
Här några bilder som gör det lättare att förstå.
http://www.tjust.com/2019/coriolis-karusell
#36 Anders Persson
Tack för länkarna. Den första ville inte eller orkade inte ladda ner sig. Den andra fick jag. Det var första bekantskapen med fenomenet för mej. Tyvärr räcker inte mina kunskaper till för att bedöma fenomenet och på vilket sätt coriolis är inblandat.
# 35 Lars Cornell
Jetkraften uppstår vid mynningen. Coriolis uppstår inuti slangen när den ligger i en båge och vätskan flödar.
En båtpropeller arbetar i stillastående vatten. I vissa sorters turbiner roterar vattnet.
Karusellen ät ett typexempel som ligger mycket nära hur jordytan röra sig tex i Uppsala.
https://www.aftonbladet.se/nyheter/a/m6P1eg/karusell-kollapsade-15-barn-skadade
Det var huvudaxeln som gick av och den är inte utsatt för några centrifugalkrafter, endast för coriolis (eller gyro) som man tydligen försummat att beräkna vid konstruktionen.
Motorns vridmoment kan kanske ha viss inverkan. Men det borde kompenseras när propellerströmmen når vingarna.
-Du får komma med någon form att källa till påståendet om corioliseffekten i vattenslangen.
– Alla mina båtpropellrar har gått framåt eller bakåt utom då jag förtöjt båten.
– Jag måste ha missförstått din tidigare beskrivning av karusellen. Den karusell jag förstod av din beskrivning var en så kallad ”bläckfisk” som är en åttaarmad bläckfisk so i ändan på armarna har en liten karusell som kan rotera åt båda hållen.
– Motorn har ett vridmoment som kompenseras av inställningen av skevrodren till exempel, Finns också andra sätt. Dessutom är motorn aningen snedställd för att kompensera propellerluftens vridning plus en kompensation som regleras på sidorodret.
#40 Guy, Här har du praktiska exempel på coriolis i vätska,
http://flodesmatarevatten.se/coriolis-massflodesmatare/
https://www.fagerberg.se/produkter/instrument/flodesmatning/coriolis-massflodesmatare/
#40 Guy and #41 Lars C.: Det är nästan 20 år sedan jag lärde känna ”Coriolis flödesmätare”. För att förklara corioliseffekten i atmosfär och oceaner lämpar sig dock denna modell mindre bra eftersom någon ”utsläckning” av centrifugalkraften, fundamental i geofysiska sammanhang, inte äger rum.
När jag kollar vad som skrivs på nätet noterar jag:
1. Flödesmätaren fungerar alldeles utmärkt
2. Just därför är det gyllene tillfällen att pytsa ut en massa tokiga förklaringar t.ex. http://eleceng.dit.ie/gavin/Instrument/Fluid%20Flow/Coriolis.htm som vinner i trovärdighet eftersom flödesmätaren fungerar så bra.
Trogen rubriken ”Corioliskraften enligt Coriolis” är det lämpligt att jag skissar hur han skulle ha förklarat ”sin” flödesmätare i termer av centrifugalkrafter som ändras vid relativ rörelse:
Vatten som strömmar genom en krökt horisontell ledning påverkas av en radiellt utåtriktad centrifugalkraft. Om en relativ rörelse injiceras i vattnet genom att den krökta ledningen rörs i vertikal led ändras styrkan och riktningen av centrifugalkraften en aning och vi får de svängningar som känsliga instrument kan registera och omtolka till flödeshastighet.
En fråga. Ett exempel på Coriolis-effekten lär vara att många floder har en hög global tio höger och en låg på vänstra sidan. Är det någon som vet något om detta?
PS, gäller floder på norra halvklotet och borde vara tydligare ju längre norrut de flyter
Sten K #43 och #44: Att corioliseffekten påverkar flodbäddar var något som till och med Albert Einstein intresserade sig för och skrev en uppsats om 1926. Se min artikel http://www.bibnum.education.fr/sciences-de-la-terre/meteorologie/albert-einstein-et-la-tasse-de-de-mme-schrodinger (engelsk version blir tillgänglig om man trycker på knappen À TÉLÉCHARGER till höger).
Han fick dock en ironisk kommentar från Max Born att han ägnade sig åt något så ”trivialt” som corioliskraften, vilket tyder på att den blivande nobelpristagaren Born trodde på Hadley’s förklaring från 1735. Se notis i American Journal of Phycis 1998 https://aapt.scitation.org/doi/10.1119/1.15162
Eftersom Einstein inte försvarade sig undrar jag om också han delade Borns villfarelse! Men hans 1926 artikel kom att ha betydelse inom meteorologin för att förklara varför lågtryck försvagas snabbade än vad som kunde förklaras med enbart markfriktionens d i r e k t a inverkan.
Ett närbesläktad fråga är om corioliseffekten när den eroderar stränderna hos floder också får dem att meandra (en av von Baers lagar). Mina experter på den hydrologiska sidan menar att det inte finns någon grund för den hypotesen. Se https://en.wikipedia.org/wiki/Baer%E2%80%93Babinet_law som också innehåller en del intressanta referenser.
#43 Sten Kaijser
Kan du precisera vad du menar: ”hög global tio höger och en låg på vänstra sidan.”
# 43 Anders P Klargjorde vad jag frågade.
#45 Anders Persson
Intressant på hur många ställen och sammanhang som coriolis kommer upp. Är det så att ingen riktigt har fått grepp om saken? Namnet tycks duga till marknadsföring av tekniska produkter också, men sådan har marknadsföringen alltid varit.
Om meandring så såg jag, för flere år sedan, en dokumentär som beskrev fenomenet med kommentar om att hur floden än ändrar sig så blir längden densamma. Tyvärr är jag inte så bra på att hitta på nätet så jag kan inte visa referenser. Jag betvivlar att det går avskilja vad coriolis skulle inverka där, om något överhuvudtaget.
Guy #47: Jo, corioliseffekten dyker upp när man minst anar det, till och med i rymden. Det är ju corioliskraften som förhindrat att man kunnat bygga och utnyttja rotationens artificiella tyngdkraft i rymdstationer av den typ vi möter i Stanley Kubriks film från 1969, ”2001 – ett rymdäventyr”. Vi möter den också i mekanismen hos två av dem fem ”Lagrangepunkterna” i och nära en planetbana https://solarsystem.nasa.gov/resources/754/what-is-a-lagrange-point/
Mycket kort sagt, och jag understryker ”mycket kort”, består mekanismen hos Lagrangepunkterna L4 och L5, de som ”behåller” det som kommit i närheten, på en liknande mekanism som på jorden, dvs ett samspel mellan centrifugalkraft och dragningskraft (gravitation). Men medan det på jorden bara är två krafter är det i samband med L4 och L5, tre krafter, förutom centrifugalkraften på föremålet, också den gravitationella attraktionen från solen och planeten ifråga.
När jag nu, för att friska upp mitt minne, läser om Coriolis artikel från 1835, påminns jag att han hela tiden talar om ”forces centrifuges composées”, dvs ”sammansatta centrifugalkrafter”, i enlighet med sin syn på ”sin” kraft som en ”utväxt” eller ”komplement” till den vanliga centrifugalkraften, eller ”force centrifuge ordinaire” som han skriver.
Anders Persson #48,49
Tack för dina svar och upplysning.
Verkar inte omöjligt med rymdstationen, men för all del är det här basics. Ca 26 min in i lektionen. https://www.youtube.com/watch?v=mWj1ZEQTI8I&t=2197s
Det låter hyfsat vad gäller sammansatta centrifugalkrafter. Styrkeskillnaden är svår att få med på en bild med vektorer då den är så liten.
Lagrangepunkterna påminde mej att satelliterna runt jorden rör sig i spiral inte cirklar. Som exemplet med kulan vid lagrangepunten. Är det spiralrörelsen som ger intryck av corioliseffekt?
Från tidigare kommenter vill jag fortfarande fråga på vilket sätt gravitationen kan ändra riktning på grund av rörelse? Långa avstånd på jorden, ok. Men korta? Så korta som en curlingbana?
Det finns kanske inga svar, så jag uppskattar all information hittills av alla här.
Tack för mej, Guy
Guy #50: Ärligt talat, jag förstår inte dina frågor. Videon handlar bara om centripetal- och centrifugalkrafterna. Vidare har ingen, vad jag vet, allra minst jag, har påstått att gravitationen ändrar rikting på grund av rörelse. Och slutligen, att som NASA (och jag) förstå lagrangepunkterna L4 och L5 ur ett ”coriolispespektiv” krävs att man frigör sig från alla populära, men felaktiga förklaringar av corioliseffekten.
Anders
Det skulle vara mycket intressant att läsa ett inlägg om din syn på klimathotet/cirkusen.
OT. Har gravitationen fart på samma sätt som ljuset? Påverkas vi av solens gravitation där solen var för 8 minuter sedan (det vi ser) eller där solen är nu (som vi ännu ej ser)?
#51 Anders Persson
Med gravitationen gällde frågan samma som i #22 och ditt svar i # 24 med den skillnaden kanske att jag inte syftade på jordens centrum utan gravitationscentrum vilket inte nödvändigtvis är samma.
Guy #54: Du liksom 90% av alla fysikaliska vetenskapsmän här i världen blandar samma ”gravitation” och ”gravity”, dragningskraft och tyngdkraft, eller snarare anser att det är samma sak. Jag gör alltid den distinktionen och jag rekommenderar att du läser om mina svar med detta i åtanke.
Lars C. #53
Men om gravitationen bara är en krökning av rumtiden kanske allt bestämdes vid big bang, som sannerligen verkar ha varit en rätt dåligt planerad händelse, om den nu ens var planerad.
#55
Nähä, nu föll jag av kälken, men tack i alla fall.
#54 Guy
Dragningskraften är den kraft som verkar mellan kroppar. Tyngdkraften är den kraft som får ett lod att peka rakt ner mot jordytan. Är inte dessa identiska? Jo, om jorden var en perfekt sfär och inte roterade.
Eftersom jorden roterar så har dessa krafter samma riktning endast på polerna och på ekvatorn. Vid ekvatorn har vi dock inverkan av centrifugalkraften att ta hänsyn till. Det gör att tyngdkraften inte är lika stor som dragningskraften – vi känner oss lite lättare (delvis beroende på att jorden inte är en perfekt sfär).
Om vi börjar springa mot öster (i rotationsriktningen) så kommer vi känna oss ännu lättare, springer vi mot väster blir vi tyngre. Det är detta som är upphovet till corioiliseffekten. Vid ekvatorn får det oss dock inte att vika av vare sig till höger eller vänster.
Vid alla breddgrader mellan polerna och ekvatorn så är pekar inte dragningskraften och tyngdkraften riktigt åt samma håll. Tyngdkraften är en kombination av dragningskraften och centrifugalkraften och centrifugalkraften pekare vinkelrätt mot jordaxeln. Vi kan dock, som Anders Persson visar i bilderna, dela upp centrifugal kraften i två komponenter, en som är i motsatt riktning till dragningskraften och en komponent som är vinkelrät mot denna. På Norra halvklotet så pekar denna rest mot ekvatorn.
Om jorden var en perfekt svär så skulle vi känna en dragning mot ekvatorn men eftersom jorden snurrat sedan urminnes tider så jorden redan anpassat sig. Jorden är ingen svär utan en tillplattad boll där tyngdkraften (kombinationen av dragnings och centrifugalkraften) pekar vinkelrätt mot jordytan.
Vad händer nu om vi står på 60:e norra breddgraden och börjar springa mot öster. Likt vid ekvatorn så kommer centrifugalkraften att öka och vi känner oss lättare – men, och det är här corioliseffekten gömmer sig. Vi hade delat upp centrifugalkraften i två komponenter, en som är vinkelrät mot jordytan och en som pekar mot ekvatorn. När centrifugalkraften ökar så ökar båda dessa komponenter – vi känner oss lättare och vi dras mot ekvatorn dvs åt höger. Skulle vi springa åt väster så känner vi oss tyngre och vi dras mot nordpolen dvs åt höger.
Det har ingenting med vem som betraktar oss när vi springer – alla kommer se att vi lutar åt höger och vi springer tillräckligt snabbt trillar.
#58 bra utredning av Johan M. Bara två kommentarer: den vertikala accelerationen, den som gör oss lättare eller tyngre, brukar kallas ”Eötvöseffekten” efter en ungersk vetenskapsman (se https://sv.wikipedia.org/wiki/Lor%C3%A1nd_E%C3%B6tv%C3%B6s eller den mer utförliga på https://en.wikipedia.org/wiki/E%C3%B6tv%C3%B6s_effect som använder en av mina artiklar som referens).
Joahn M:s slutmening är central. Den understryker att vi kan inte behandla corioliseffekten på en roterande planet på samma sätt som på en platt karusell, eftersom den förra, till skillnad från den senare, INTE är en tröghetsrörelse.
Johan M #58
Ett par kommentarer.
”Eftersom jorden roterar så har dessa krafter samma riktning endast på polerna och på ekvatorn. Vid ekvatorn har vi dock inverkan av centrifugalkraften att ta hänsyn till. Det gör att tyngdkraften inte är lika stor som dragningskraften – vi känner oss lite lättare (delvis beroende på att jorden inte är en perfekt sfär).”
Menar du att tyngdkraft = dragningskraft – centrifugalkraft eller någon annan liknande kraft? Så en hovrande helikopter känner ingen tyngdkraft?
Jag kan inte se det så.
”Vad händer nu om vi står på 60:e norra breddgraden och börjar springa mot öster. Likt vid ekvatorn så kommer centrifugalkraften att öka och vi känner oss lättare – men, och det är här corioliseffekten gömmer sig. Vi hade delat upp centrifugalkraften i två komponenter, en som är vinkelrät mot jordytan och en som pekar mot ekvatorn. När centrifugalkraften ökar så ökar båda dessa komponenter – vi känner oss lättare och vi dras mot ekvatorn dvs åt höger. Skulle vi springa åt väster så känner vi oss tyngre och vi dras mot nordpolen dvs åt höger.”
För att än en gång ta upp karusellen, som är usel som exempel, så se 60N breddgraden som en skiva vars ytterkant vi står på jämt med skivans plan. Centrifugalkraften pekar utåt längs skivans plan och dragningskraften (gravitationen) pekar i ca 60 graders vinkel under skivan mot fortsättningen på skivans axel. Med dessa två komponenter ser jag en kraft som vill dra oss mot ekvatorn. Detta oberoende åt vilket håll näsan pekar. Jag förstår att vikten ökar eller minskar på grund av ökad/minskad centrifugalkraft. Wikipedias exempel med flygplan var rätt konstigt. Det måste flyga väldigt lågt om det inte tänker ändra breddgrad. På hög höjd följer den med rotationen från en annan ”skiva” av jorden.
Tack i alla fall. Var dag lär man sig något nytt.
#60 Guy: tyngdkraft = dragningskraft + centrifugalkraft, men eftersom de pekar åt lite olika håll kommer den senare att försvaga den förra.
Det går inte att använda karusellen för att förstå vad Johan M. skrev, eftersom någon planetär gravitation med någon snedställd vinkel mot plattformen inte existerar.
Anders Persson # 61
Jag tror du missförstår mej eller så har jag missförstått johans beskrivning eller centrifugalkraftens riktning på en roterande skiva skuren längs 60 breddgraden med joraxeln som axel. På skivans periferi verkar en dragningskraft/ gravitation som går i ca 60 graders vinkel mot jordaxeln under skivan.
Tyvärr har jag inte möjlighet att rita vad jag menar. En bild kan säga så mycket där orden lätt missförstås.
Guy #60 och #62: Du skrev: ”Centrifugalkraften pekar utåt längs skivans plan och dragningskraften (gravitationen) pekar i ca 60 graders vinkel under skivan mot fortsättningen på skivans axel. Med dessa två komponenter ser jag en kraft som vill dra oss mot ekvatorn.”
Svagheten i det du skrev var ordet ”ca” = ”cirka”. Gravitationen har, pga jordens icke-sfäriska form en komponent som pekar inåt, mot jordaxeln och exakt balanserar den utåtriktade centrifugalkraften. Vore det inte så skulle jorden fortsätta att deformeras.
Anders Persson # 63
Ja jag skrev cirka för att gravitationscentrum är kanske inte riktigt där jordens medelpunkt befinner sig. Centrifugalkraften borde, enligt min mening, vara i plan med den skiva som man skär vid 60 graders cirkeln. 60 graders cirkeln roterar runt jordaxeln men inte runt jordcentrum vilket ekvatorn gör. Därför blir det en liten skillnad där centrifugalkraften lutar mot ekvatorn och dragningkraftens linje går från jordens gravitationscentrum genom samma punkt men litet norrom centrifugalkraftens vektor.
Bättre kan jag inte förklara min mening.
Guy #64: Men är det inte vad du ser på några av mina bilder ovan med jorden i genomskärning???
#64 Guy. ”gravitationscentrum är kanske inte riktigt där jordens medelpunkt …”
Jag trodde att det var definitionsmässigt samma sak.
Guy, går jordaxeln genom gravitationcentrum eller genom jordens medelpunkt eller kanske något annat?
Anders Persson #65
Visst Anders, i bil 4. Vad jag inte fattade var wikis artikel och bolderna med springande, flygande öst och väst där viktökningen plötsligt ändrar skeneriet.
Lars Cornell # 66
Jag kan tänka mej att jordens rotationsaxel går genom gravitationscentrum, kanske också genom medelpunten. Men kan någon berätta var jordens masscentrum befinner sig? På månen är det kanske lätt att precisera var jordens gravittionscentrum befinner sig, men på jorden har vi en massa olika starka gravitationsfält. I stort sätt dras allt mot den största massansamlingen vad jag förstår.
Jordens gravitationscentrum eller masscentrum ligger i den geometriska mittpunkten. Så långt är allt gott och väl. Med dragningskraften, gravitationskraften, på ett föremål på jordytan bestäms av ALL massa i dess närhet. En följd av detta är att det är bara på polerna och vid ekvatorn som dragningskraften pekar exakt mot jordens mittpunkt, i övrigt pekar den en aning åt sidan, en aning ”hitåt”.
Man kan förstå detta kvalitativt om man tänker sig en planet med en massfärdelning som en doughnut (ringformad bulle eller munk) där ju masscentrum ligger i den geometriska mittpunkten, men där gravitationsvektorn på de flesta ställen på planetens yta pekar åt annat håll.
#59 Anders Persson
”..den vertikala accelerationen, den som gör oss lättare eller tyngre, brukar kallas ”Eötvöseffekten” ..”
Tittade på den engelska beskrivningen och det enda man kan säga är – Wow!! Jag hade gissat att denna effekt var svårmätbar vid låga hastigheter om man inte satte upp ett experiment med laserprecision. Då visar det sig att Eötvös kunde påvisa den med tyngdmätare på fartyg som gick i östvästlig riktning och det redan 1908. Man kan inte annat än imponeras.
Anders Persson #68
”Jordens gravitationscentrum eller masscentrum ligger i den geometriska mittpunkten. Så långt är allt gott och väl. Med dragningskraften, gravitationskraften, på ett föremål på jordytan bestäms av ALL massa i dess närhet. En följd av detta är att det är bara på polerna och vid ekvatorn som dragningskraften pekar exakt mot jordens mittpunkt, i övrigt pekar den en aning åt sidan, en aning ”hitåt”.”
Det är tydligt att vi talar om samma sak. Det är krafternas riktning som är problemet. Dock inte riktningen på dragningskraften eller gravitationen.
Jag tycks inte kunna förklara vad jag menar. Jag tycks också ha problem med att förstå. Till exempel vad menas med ”en aning hitåt”
Testades Eötvöseffekten någonsin på flygplan? i Wiki -texten talas om fartyg och fartyget har ”direkt kontakt till en roterande jord och den tröghet det medför. Det har diskuterats i tidigare coriolisdiskussioner, också i samband med den friktionsfria rörelsen.
#70 Guy: Friktionen med jorden är irrelevant när det gäller både corioliseffekyten och eötvöseffekten. Det är ett vanligt missförstånd, under de senaste 150 åren, att en kropp måste ha friktionskontakt med jorden för att ”veta” att den befinner sig på en roterande planet. Den nödvändiga informationen ligger i att gravitationsvektorn inte är vinkelrät mot jordytan, utom vi polerna och ekvatorn.
#69 Johan. Ja det är bara att imponeras. Hur gjorde de?
Jordytan lutar i genomsnitt 2 m per km (21 km/10000 km) och det är rätt mycket.
Lutningen 2 mm per meter åstadkommer en rullkraft som är fullt mätbar.
https://sv.wikipedia.org/wiki/Eötvöseffekten
Anders Persson # 71
”Med dragningskraften, gravitationskraften, på ett föremål på jordytan bestäms av ALL massa i dess närhet.”
”Den nödvändiga informationen ligger i att gravitationsvektorn inte är vinkelrät mot jordytan, utom vi polerna och ekvatorn.”
Din första mening kan utesluta den andra meningen. ALL massa i näheten bestämmer gravitationsvektorn. I stort är vektorn vinkelrät mot periferins tangent där du för tillfället befinner dig. Står du på sydpolen, med all bergsmassa under och bredvid dig, påverkas vektorn kanske minimalt men centrifugalkraften saknas. Men är det ens mätbart?
Det intressanta är centrifugalvektorn, som alltid är vinkelrät mot rotationsaxeln och därför ger en kraft mot ekvatorn inte mot polerna.
Guy #73: Nä, meningarna utesluter inte varandra. Bara om planeten är en perfekt sfär gäller din invändning. Men det är inte jorden varför varje föremål, utom vid polerna och ekvatorn påverkas av en samlad dragningskraft från en massa som från föremålet sett är en aning asymmetriskt fördelad.
#72 Lars Cornell
De engelska sidorna beskriver hur de gick till väga. Eötvös mätte inte den avböjande kraften utan skillnaden i tyngkraften (vilket också fick hans namn) . För ett fartyg som stävar österut vid ekvatorn med en fart av 10m/s (20 knop) och sedan vänder och stävar väster ut så är skillnaden i tyngdkraft för ett 10kg lod motsvarande 3 gram. Försök att mäta det på ett fartyg som rullar, jag har svårt att hälla uppe en kopp kaffe
https://en.wikipedia.org/wiki/E%C3%B6tv%C3%B6s_effect
#75 Jahan M. Det väcker många tankar. En bragd var det under alla omständigheter.
#75 + #76: Eötvöseffekten visar också betydelsen av att hälla rågången ren mellan klassisk och modern fysik. Den moderna fysiken lär oss att för föremål som närmar sig ljusets hastighet ökar den gravitationella tyngden ökar, därför att massan ökar. Men Eötvöseffekten visar att tyngden, men nu den icke-gravitationella, ökar för helt måttliga hastigheter. I förra fallet ökade massan, men i det senare.
Ett liknande fall är Einsteins hiss där det sägs att det är omöjligt att avgöra om den står stilla eller accelereras i tomma rymden, i bägge fallen ”känns” acclerationen mot hissens golv likadant. Därför går det inte att avgöra om man är i en hiss på marken (utan fönster) eller en som accelerar i rymden (också utan fönster).
Men det kan man faktiskt. Står man stilla in den jordbundna hissen kan man i princip mäta upp att tyngdkraften i olika delar inte är parallell, utan kraftlinjerna konvergerar. Man kan också genom att putta ett föremål längs golvet se att det på jorden avlänkas av en corioliskraft.
Anders Persson #77
Om hissen står ”stilla” i rymden är den i ”fritt” fall och du känner ingen acceleration. Acceleration känner du. Om du känner acceleration vet du inte om det beror på gravitation eller om du accelererar.
#78 Guy: Jo, det vet jag av skäl som angavs ovan. Einsteins tankeexperiment utgår från att gravitationens kraftlinjer är parallella. Men på varje planet, roterande eller ej, är de konvergerande. Roterar sedan planeten ”avslöjar” den sig på det sättet. Einsteins tankeexperiment är alltså lite överidealiserat.
Anders – en/två fråga(or) om corioliseffekten.
När vi ändrar hastighet i öst-västlig riktning så är det naturligtvis så att vi får en corioliseffekt. Hur förstår man kraften när vi gör en förändring i nord-sydlig riktning. Är det då den högre (eller lägre) rotationshastigheten som gör att vi får en kraft som är vinkelrät mot rörelseriktningen när vi rör oss mellan breddgraderna? Skulle vi ha en corioliseffekt i nord-sydlig riktning om jorden var en roterande cylinder?
#80 Johan M.: Jag har inget bra svar på din första fråga. Jag är inte säker, men jag tror, att medan corioliseffekten för ost-västlig rörelse beror på att centrifugalkraften ändrat sin styrka, men bevarat sin riktning, har den vid nord-syd rörelse bevarat sin styrka, men ändrat riktning. Se den inledande schematiska figuren.
På fråga 2 kan jag säga att med en planet som roterande cylinder får vi ingen balans mellan gravitation och centrifugalkraft, som vi får på en roterande planet, vars form ju just bestäms av rotationen.
#81 Anders Persson
Vid en nord-sydlig riktning så ser jag hur vi får en förändring i vår ”tyngdkomponent” och även en förändring i den dragning mot ekvatorn som vi har. Dock så ser jag inte att vi skulle få någon förändring vinkelrätt mot rörelsen. Är det inte Hadley som kommer in här och får vår rörelse att böja av i rotationsriktningen vilket skulle ge oss den vinkelräta komponent vi söker? I sidorna på SMHI säger du att Hadley endast gav 50% av effekten, är detta de 50%?
Hej Johan M,
Coriolis-vektorn är ”parallell med” rotationsvektorn. Det finns ingen Coriolis-effekt för en rörelse parallell med C-vektorn. (kryssprodukten är 0)
Sten #80: Jag förstår inte. Corioliskraften (per massenhet) skrives 2Omega x Vr, där Omega är rotationsvektorn och Vr relativa rörelsen. Vad skulle ”coriolisverktorn” vara? Sant är att en rörelse längs med cylindern inte genererar någon corioliskraft, men väl all annan rörelse. Men eftersom cylinderns form inte är bestämd av rotationen har gravitationen från cylindern ingen chans att släcka ner centrifugalkraften, som kommer att dominera. Men corioliskraften, om än liten, finns där.
Hej Anders Persson,
när jag talar om Coriolis-vektorn menar jag helt enkelt 2 x rotationsvektorn. Rotationsvektorn ger ju ”total information” om rotationen, riktning och rotationshastighet.
Johan M ställde den ”kontrafaktiska” och fysikaliskt omöjliga frågan om det skulle finnas en Corioliseffekt vid nord-sydlig rörelse om jorden vore en roterande cylinnder. Jag tolkade hans fråga som att cylinderaxeln och rotationsaxeln var samma axel. I princip kan man väl besvara Johan M’s fråga med att notera att en nord-sydlig rörelse vid ekvatorn inte har någon ”märkbar effekt”
Sten #85: Nord-sydlig rörelse har ingen (0%) effekt överhuvudtaget, vare sig på jorden eller på den roterande cylindern eftersom rörelsen är parallell med rotationsvektorn.
Mitt exempel med en cylinder var dumt.
Det jag inte förstår är hur vi vid en nord-sydlig riktning kan få en kraft som blir vinkelrät. Om vi från ekvatorn skjuts norrut så kommer vi få en ökad centrifugalkraft. Vi kan bryta upp den i en kraft som är vinkelrät mot jordytan och en som är riktad mot ekvatorn – detta på samma sätt som om vi skjuts mot öster.
Vi har dock ingen komponent som får oss att böja av åt höger.
Om man däremot följer Hadleys model och räknar med att man behåller sin högre östliga hastighet när man färdas norrut så får vi en avböjning mot öster eftersom jordens radie blir mindre. När vi väl färdas snabbare åt öster får vi en corioiliseffekt som får oss att böja av mot söder osv?
Jag håller visst på att bli snurrig. Får inte det här att gå ihop.
– Kanske någon kunde förklara vad en rotationsvektor är. Av #85 Sten K. fick jag intrycket att
rotationsvektorn är i rotationsriktningen. Se # 86 där nord-sydlig riktning är parallell med
rotationsvektorn.
– Hur kan centrifugalkraften bli större om vi flyttar oss norrut från ekvatorn. # 87
#87 Johan M och #88 Guy: Som jag skrev i #81 så ändrar centrifugalkraften, vid nord-sydlig rörelse, sin riktning och det ger en avlänkning åt höger. Jag hänvisade till första bilden i min artikel. Har ni kollat den?
Hadley’s model antar att den absoluta hastigheten bevaras. Han har ingen uppfattning om avståndet till jordaxeln. Men det har man i en alternativ model, bevarandet av impulsmomentet, dvs produkten av ost-västlig rörelse (U+u) och avståndet till jordaxeln (R), (U+u)*R där U är jordens hastighet österut och u föremålets. Antar vi att i begynnelsen rörelsen bara är in nord-syd riktning (och noll i ost-väst, u=0), så kommer det att genereras en hastighetsförändring, acceleration, till höger på NH.
(U+0)*R = (U+u)*(R-dR) där dR är hur mycket närmare vi kommit jordaxeln.
Hadley’s model är fel på många sätt. Bla. så kommer den absoluta hastigheten av en kropp som friktionsfritt rör sig över jordens yta att variera, medan den relativa är konstant. I Hadley’s fall, med bevarad absolut hastighet ökar den relativa hastigheten, ofta till orealistiskt stora värden.
Anders Persson # 89
Visst har jag kollat din bild. ”An object moving inwards”. dvs du minskar radien men behåller periferihastigheten, eller ser jag fel?
På globen rör vi oss inte inwards om vi går mot norr och centrifugalkraftens riktning är vinkelrät ut från rotationsaxeln. På väg mot mindre periferihastighet minskar centrifugalkraften. Vad missar jag?
#90 Guy: Det viktiga är den totala centrifugalkraften, dvs den som visas på bilden. Den ändrar riktning eftersom rörelsens trajektoria, till vilken centrifugalkraften ju är vinkelrät, inte länge följer en latitudcirkel.
#89 Anders Persson
ok, fig 1 är jag nu med på men det är klurigt att översätta den i huvudet till en sfär och att det egentligen beskriver en nordlig förflyttning.
Johan M # 92
Jag får inte bilden till en sfär med bästa vilja i världen. Dessutom är rörelsens riktning inåt! Att byta latitud är inte att gå inåt. Tänk dej jorden som en packe skivor staplade på varann från ekvatorn upp. Varje skiva uppåt har samma rotationshastighet som den underliggande men den perifera hastigheten är mindre och följaktligen är centrifugalkraften mindre.
Anders Persson # 91
Rörelsens riktning är inåt på bilden. På jordens sfäristka yta är den inte inåt, om du inte räknar med dom där 42km som jorden är bredare vid ekvatorn.
Av din bild får man intrycket att coriolisvektorn är i tangentens riktning om gravitationen skulle ha släppt taget just där. Inåt kunde testas med en dykande ubåt.
Till alla: Fördelen med George Hadley’s förklaring är att den är mycket enkel att förstå. Därför finns den i nästan alla meteorologiböcker, även i en del akademiska sådana. Den presenteras bredvis ekvationer som beskriver något helt annat, som inte är exakt lika lätt att förstå i ett nafs.
Vad är nu problemen? Hadley’s model ger ett värde på corioliskraften som bara är hälften av den verkliga. Den kan bara användas för nord-sydlig rörelse och får att det framstå som att inget sker för ost-västlig. Till sist stipulerar den att den absoluta hastigheten är konstant, medan den i verkligheten varierar.
Men undervisningen i dynamisk meteorologi är nu sådan på de flesta ställen in världen: studenterna får korrekt härleda en matematisk relation som sedan ges en ”lättförklarlig” tolkning som inte rimmar med matematiken.
Studenterna, åtminstone sådana som jag, tolkar det som att atmosfären är komplicerad, professorna väldigt klipska och lilla jag alltför dum för att förstå något. Därför lika bra att lära sig allt utantill och inte fråga ”varför”.
Det var så jag efter två försök, i det tredje klarade tentan i mars 1967. Då hade en av lärarna på MISU pikat mig: -Jasså, du är en sådan där som frågar ”varför”.
Anders Persson #,+ 86
utom vid ekvatorn är inte nord-sydlig rörelse på jorden parallell med rotationsvektorn, men det noterade du ju i en senare kommentar.
Anders Persson #,+ 86
utom vid ekvatorn är inte nord-sydlig rörelse på jorden parallell med rotationsvektorn, men det noterade du ju i en senare kommentar.
Och stort tack för ett fantastiskt bra inlägg!
”Studenterna, åtminstone sådana som jag, tolkar det som att atmosfären är komplicerad, professorna väldigt klipska och lilla jag alltför dum för att förstå något. Därför lika bra att lära sig allt utantill och inte fråga ”varför”.”
Har aldrig klarat att lära mig utantill. Därför blir det ”varför” på grund av nullius in verba.