Genom Gösta Petterssons eminenta analys i boken Falskt Alarm har bombkurvan blivit ett hett diskussionsämne här. Bombkurvan visar hur mängden av den radioaktiva koldioxid, som tillfördes atmosfären på grund av kärnvapenprov i atmosfären, avtar efter det att proven upphörde 1963. Men Bolins och Erikssons klassiska matematiska modell från 1959 stämmer inte med den observerade kurvan.
Vi har diskuterat Gösta Petterssons bok och bombkurvan i flera olika inlägg här på bloggen: Det var ett gästinlägg av Gösta Pettersson, Boken Falskt alarm – läs och begrunda! och därefter Klimatsimuleringar och observationer strider mot varandra: Bombprovskurvan samt Bombkurvan en gång till.
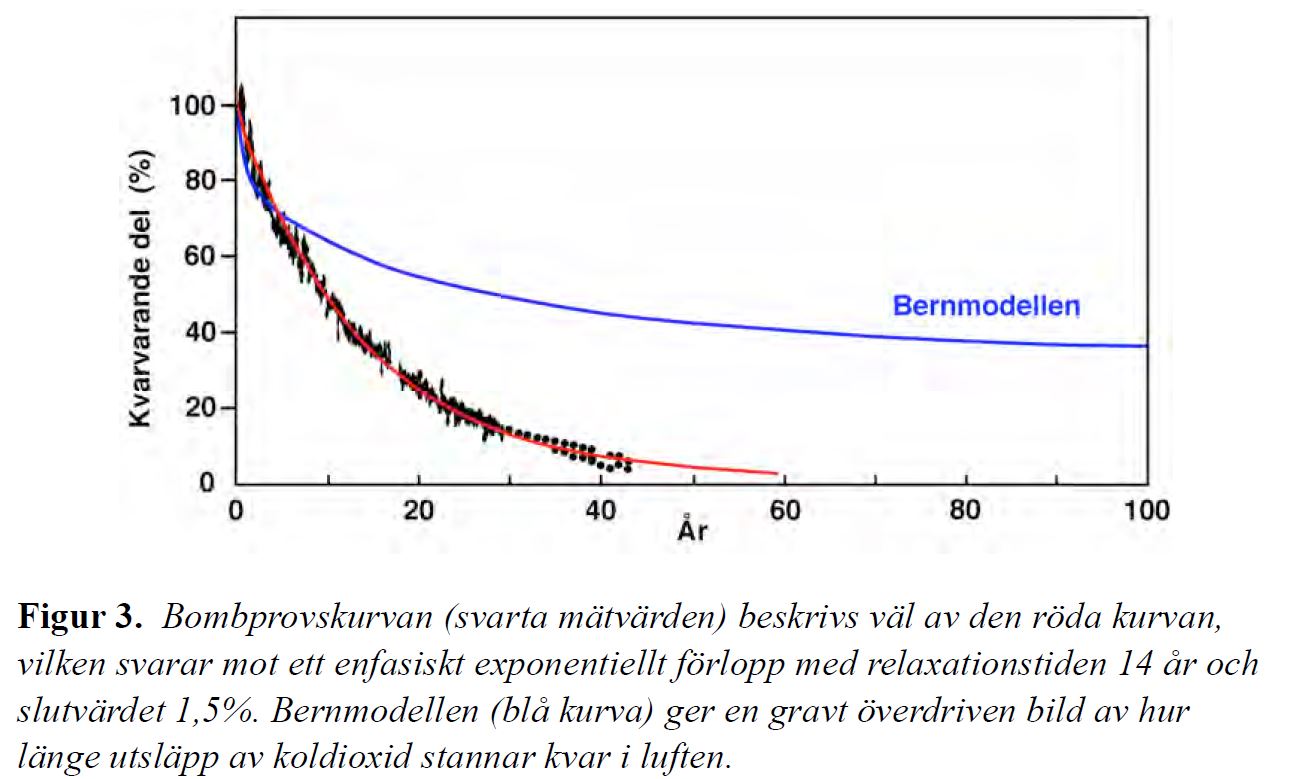
Figuren från Gösta Petterssons bok ovan visar hur bombkurvan, som beskriver hur en puls av radioaktiv koldioxid minskar efter att bombproven upphört, skiljer sig från Bernmodellens motsvarande simulerade kurva, som visar hur en puls av antropogen koldioxid minskar efter att utsläppen upphört.
Vid alla de nämnda blogginläggen har vi haft intensiva diskussioner i kommentarsfältet om bombkurvan falsifierar Bernmodellen eller inte. En del anser att kurvorna faktiskt skall vara så olika som de är medan andra, inklusive jag själv, anser att bombkurvan och Bernkurvan borde likna varandra mera och att Bernmodellen alltså falsifieras av olikheten.
Vi vet att Bernkurvan ser ut som den gör mycket beroende på Revelleeffekten som bland annat är orsaken till att Bernmodellen visar att det blir mer än 20% kvar av koldioxidutsläppet under tusentals år. Revelleeffekten innebär att havets förmåga att ta emot av människan utsläppt koldioxid är mindre än en tiondel än vad den skulle vara utan Revelleeffekt. Bombkurvan visar ingenting sådant. Men är detta rätt eller fel, skall bombkurvan visa denna och/eller andra konsekvenser av Revelleeffekten eller inte?
Bolin och Eriksson (1959) (se referenser nedan) har i sin klassiska artikel tagit fram en teori och en matematisk modell för hur mängden radioaktiv koldioxid i luften påverkas av antropogena utsläpp av fossil koldioxid. Den matematiska modellen bygger på att klimatsystemet antas bestå av atmosfären, havets omblandade skikt och djuphavet därunder. Låt oss betrakta hur Revelleeffekten skulle påverka för enkelhetens skull enbart atmosfären och det omblandade skiktet.. Vi antar att dessa är ungefär lika stora kolreservoarer.
Anta att i jämvikt representeras den vanliga koldioxiden av 10000 vita bollar i atmosfären och 10000 vita bollar i havets ytskikt medan den radioaktiva koldioxiden motsvarar 100 svarta bollar i vardera atmosfären och havets ytskikt. Antag att vi på grund av bombprov skulle tillföra mer radioaktiv koldioxid till atmosfären så att de svarta bollarna i atmosfären skulle fördubblas. Om ingenting annat skulle ändras efter att bombproven upphört så skulle de 100 extra bollarna minska i atmosfären och öka i ytskiktet tills vi skulle ha 150 svarta bollar vardera i dessa. Vi skulle få en perfekt exponentiellt avklingande bombkurva. En del av diskussionsdeltagarna här menar att detta är förklaringen till bombkurvan.
Men Bolin och Eriksson var ute efter något annat, nämligen hur Revelleeffekten påverkar de svarta bollarna. De tänkte inte på någon bombkurva eftersom denna inte var aktuell vid denna tid. Revelleeffekten innebär att när vi tillför ett stort tillskott av koldioxid så kommer denna inte att fördela sig jämnt mellan atmosfär och ytskikt. Orsaken är att koldioxiden påverkar pH i havet. I stället kommer mycket mer av överskottet att hamna i atmosfären än i havet. Låt oss anta att Revellefaktorn är lika med 10, varvid tio gånger mer hamnar i atmosfären. Om vi då tillför fossil koldioxid som vi representerar med 1100 röda bollar så kommer vid jämvikt 1000 röda bollar att hamna i atmosfären och endast 100 i havets ytskikt. Vi får då totalt 11000 vita och röda bollar i atmosfären och 10100 bollar i ytskiktet så att det därigenom blir fler bollar i atmosfären än i ytskiktet.
Vad Bolin och Eriksson påpekade var att detta måste påverka även de svarta bollarna eftersom radioaktiv koldioxid är i snabbt inställande jämvikt med vanlig koldioxid. Därför kommer även de svarta bollarnas fördelning att ändras så att de fördelas mellan atmosfär och ytskikt i proportionerna 11000:10100. Då blir det 104 svarta bollar i atmosfären och 96 i havets ytskikt. Revelleeffekten bidrar alltså till att mängden radioaktiv koldioxid ökar i atmosfären.
Å andra sidan så minskar förhållandet mellan mängd svarta bollar och röda och vita bollar i atmosfären. 104/11000 är mindre än 100/10000. Detta illustrerar att när människan släpper ut fossil koldioxid till atmosfären så minskar förhållandet mellan radioaktiv och vanlig koldioxid. De vanligaste fossila bränslena är så gamla att allt radoaktivt kol har avklingat. Därför är fossil koldioxid praktiskt taget fri från radioktiv koldioxid. I princip kan man därför se minskningen i förhållandet radioaktiv till vanlig koldioxid som ett mått på hur mycket fossilt kol som har släppts ut. Det är denna minskning som kallas för Süesseffekten.
Om vi går tillbaka till resonemanget om bombkurvan och tänker oss att under den tid som de svarta bollarna minskar i luften och ökar i havets ytskikt så släpper vi också ut antropogen koldioxid. Vartefter det blir mer och mer röda bollar så kommer den jämviktsfördelning som de svarta bollarna strävar mot att förskjutas. På slutet vid den nya jämvikten kommer det att vara fler än 150 svarta bollar i atmosfären och färre i havets ytskikt. Bombkurvan kommer enligt detta resonemang att bli deformerad jämfört med en ren exponentiell avklingning.
Bolin och Eriksson utvecklade en matematisk modell som beskriver de processer som vi beskrivit ovan med vita, röda och svarta bollar, men för alla de tre reservoarerna atmosfär, ytskikt och djuphav. Modellen sammanfattas som differentialekvationssystemet (36) tillsammans med ekvation (35) (se fördjupningsrapporten i referenslistan nedan). De använde modellen för att beräkna hur stor Süesseffekten borde ha blivit, dvs. hur mängden radioaktiv koldioxid i luften hade ändrats på grund av utsläpp av fossil koldioxid fram till 1954.
Jag har använt samma modell men nu för att beräkna hur mängden radioaktiv koldioxid ändrats sedan 1963, dvs. jag har beräknat hur bombkurvan borde se ut enligt Bolins och Erikssons teori och matematiska modell. Jag har redovisat detaljerna om hur jag gjorde detta i den fördjupningsrapport som finns i referenslistan.
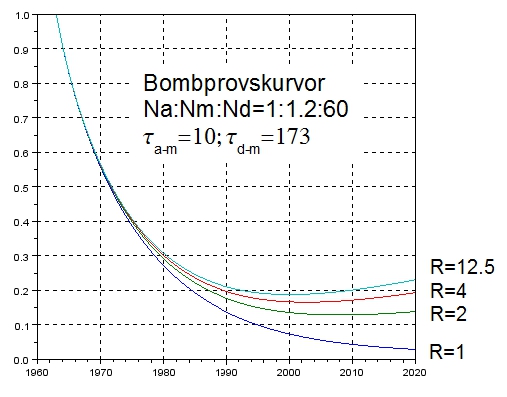
Jag har gjort samma antaganden som Bolin och Eriksson att förhållandet mellan reservoarerna atmosfär, havets ytskikt och djuphav är 1:1.2:60. Beräkningarna gjordes för olika värden på Revellefaktorn, från ingen Revelleeffekt då faktorn är ett, till maximal enligt Bolin och Eriksson då Revellefaktorn är lika med 12.5. Jag fick följande resultat där R står för Revellefaktorn.
Endast genom att anta att det inte finns någon Revelleeffekt, R=1, får vi en bombkurva som nära liknar den observerade. Även med så liten Revelleeffekt som R=2 så blir den beräknade bombkurvan starkt deformerad på grund av utsläppen av antropogen koldioxid. Den gradvisa ökningen av antropogen koldioxid i klimatsystemet motverkar minskningen av radioaktiv koldioxid och till slut börjar denna till och med öka. Med den nivå av Revelleeffekten som Bolin och Eriksson kom fram till skulle ökningen ha börjat redan omkring år 2000.
Fler beräkningar med diskussion finns i fördjupningsrapporten. Resultaten väcker frågor om Revelleeffekten. De beräkningar jag har gjort antyder att Bolins och Erikssons teori och modell, enligt vilken R=12.5, inte stämmer med den observerade bombkurvan. Men jag har naturligtvis bara skrapat på ytan, detta är ingen genomarbetad vetenskaplig undersökning.
Av de senaste jordsystemmodellerna, som är både klimatmodeller och kolcykelmodeller, bör man enligt min mening kunna kräva att de skall simulera bombkurvan så att man genom att jämföra med den observerade bombkurvan kan testa hur bra deras fysik stämmer med verkligheten. Var och en som har möjlighet att påverka de som utvecklar sådana modeller borde framföra detta krav. Jag kan inte se att det finns någon ursäkt för att ett sådant krav inte skulle vara standard för sådana modeller.
Om det skulle visa sig att Revelleeffekten faktiskt inte är verksam i naturen skulle detta radikalt förändra förutsättningarna för hela klimatfrågan.
Referenser
Gösta Pettersson, 2013, Falskt Alarm.
Bolin, Bert, and Erik Eriksson (1959). ”Changes in the Carbon Dioxide Content of the Atmosphere and Sea Due to Fossil Fuel Combustion.” In The Atmosphere and the Sea in Motion, edited by Bert Bolin, pp. 130-42. New York: Rockefeller Institute Press. Online here.
Revelle R, Süess HE,1957. Carbon dioxide exchange between atmosphere and ocean and the question of an increase of atmospheric CO2 during the past decades. Tellus 9:18-27.
Pehr Björnbom, 2013, Fördjupningsrapport om simuleringar av bombkurvan med Bolins och Eriksson matematisk modell.





Tack Pehr, det där är viktigt. Gösta Petterssons iaktageler är intressanta. ”finner man att IPCC:s spådomar om framtida koldioxidhalter och temperaturer överskattats med en faktor mellan 3 och15 …. Skäl nog att helt underkänna IPCC:s spådomar och syn på verkligheten …”
Men varför beaktas bara utbytet med hav och inte även flödet via fotosyntes på land?
Tack Pehr Bj. för denna genomgång! Nu känns det som om det är möjligt att få lite, lite grepp om vad det handlar om. Som betraktare vid sidan om vad beträffar klimatfrågans hårddata har jag slagits av att Lennart Bengtsson inte tycks vilja ta i just den här delen av klimatfrågan. Han går med på att klimathotsskeptikerna har fått rätt än så länge, men vänta bara i framtiden slår AGW till och det beror på koldioxidens långa uppehållstid. I den här delfrågan uppträder han som om ”science is settled”. Ingen diskussion.
Sista halmstrået eller spiken i kistan för AGW hur man nu ser det?
Murray Salbys föredrag i Hamburg 18 april om Model world och Real world.
Se sista 10 minuterna bör ses.
http://www.youtube.com/watch?v=2ROw_cDKwc0
OT: Underhållande inlägg från ”Donnan” om det stundande IPCC-mötet i Stockholm:
http://nofrakkingconsensus.com/2013/06/13/the-ipcc-politicizing-science-since-1988/
Wow! När jag läste din förklaring om bollarna tänkte jag att detta verkar ju inte klokt! Det skulle ju innebära att tillfört kol i atmosfären mer eller mindre ”magnetiskt” drar till sig kol från havet. Sedan visar du i grafen att Bolins ekvation faktiskt ger det falska utslaget.
Om alla klimatmodelllerare använt denna ekvation som utgångspunkt så förklarar det varför deras modeller efter en (kort) tid sticker iväg på tok för högt jämfört med uppmätta värden.
Jag tror att du åstadkommit något riktigt minnesvärt Pehr!
Olaus: Jämför Murray Salbys slutkläm med Richard Feynman i en föreläsning om vetenskaplig metod http://www.youtube.com/watch?v=EYPapE-3FRw
Revelleefffekten kan ju existera tillammans med fysikaliska faktum. Den koldioxidmängd som nederbörd tvättar ut atmosfären är av samma storleksordning som utspädning visad av bombkurvan. Den sjunkande kallvattenmängden vid polerna har också samma storleksordning. Att koldioxidmättad nederbörd som hamnar i oceanernas ytvatten styrs av revelleeffekten leder ju till att bombkurvan indikerar att fler samband måste finnas. Oceanernas djupvattenströmmar har en mycket lång omloppstid, men mängden koldioxid
de innehåller, når alltid ytan och med en halt c14 som fanns när flödet sjönk ner från ytläget.
Skillnaden i koldioxids löslighet i kallt sjunkande vatten och varmt tropiskt är 2:1. Även om djupvattenströmmarnas storlek är vagt bestämda så tyder nuvarande vetande på att deras transporterade volym är mycket stor.
Förstår jag det rätt om i det andra diagrammet det visas absolut mängd C-14 medan i första diagrammet visar på andelen av allt kol som är C-14? Detta ger en betydande skillnad eftersom CO2 halten stigit så mycket. Som Pehr påpekar får man den där stigningen i slutet enbart om man tittar på absolut mängd, inte på andel.
I vilket fall som helst kan man konstatera att Pehrs nuvarande analys inte stämmer överens med Gösta Petterssons från första figuren.
Bra fråga Thomas,
Pratar vi mängder eller halter här? Vad säger egentligen bombkurvan? Kvarvarande del (%), menas då kvarvarande mängd (antal molekyler, massa) i % av det som släpptes ut? I så fall stämmer Pehrs slutsats. Annars måste man räkna om så att det är samma enheter som jämförs. Själva resonemanget är väl riktigt i alla fall.
Sven Östholm2013/06/14 kl. 10:28
”Revelleefffekten kan ju existera tillammans med fysikaliska faktum. ”
Vad betyder det? Kan, under vilka förutsättningar? Finns det belagt eller är det en teori?
Varifrån får du att bombkurvan visar på utspädning och inte på kolets omsättning i kolcykeln?
Veckorapporten från vetenskapens värld(P1) förklarar klyvöppningsmetoden och den snabba skiftningen som kunde noteras. Dvs olika förklaringar ges. Haven är med!
Bombkurvan förklaras?
Thomas och charlie, bombkurvorna i den första och den andra figuren är uttryckta i samma enheter. Jag har naturligtvis insett att det är viktigt att se till att använda samma enheter eftersom det blir svårt att jämföra annars.
Att utspädningen, eller som du föredrar att benämna den omsättningen, inte kan förklaras med revelleefekten är ju utgångspunkten. Hade revelleeffekten gett förklaring på hur c14 halten från bombproven sjunkit så vore ju frågeställningen redan besvarad.
Att halten c14 från bomproven minskar måste bero på att atmosfärens koldioxid växlas mot koldioxid med mindre halt c14 från en tillräckligt stor depå, förslagsvis uppvällande djupvatten. Mängden uppvällande djupvatten bör rimligen motsvara mängden som sjunker vid polerna och de kända djupvattenströmmarna transporterar en årlig volym som motsvarar den koldioxidmängd med låg c14 halt som krävs för att ge bomkurvans avklingade c14 halt.
En ganska bra redogörelse för analys av klyvöppningarnas variation ges i bifogad länk.
http://www.geocraft.com/WVFossils/stomata.html
Så vitt jag kunnat konstatera så finns inga tunga invändningar mot gjorda slutsatser. Ett för IPCC del besvärande faktum är att den gissning om ”förindustriell” koldioxidhalt som IPCC gjort förfaller vara fel. Den fix som gjorts vid tolkning genom att förskjuta borrkärnornas mätvärden 80 år verkar vara ett tragiskt misstag.
Sven Östholm, jag har också funderat i de banorna som du skildrar i dina kommentarer här. De processer som du tar upp kan inte beskrivas med de enkla modeller som Bolin och Eriksson använde sig av.
De nya jordystemmodellerna med kolcykel skulle i princip kunna ge en riktig beskrivning men vad som talar emot är att processerna är så komplicerade och dessutom delvis kaotiska och så pass lite är känt om dem. Ett test på dessa modeller som man som sagt i blogginlägget borde kunna kräva att man visar jämförelsen mellan modellens bombkurva och den observerade bombkurvan.
Pehr,
Jag köper din förklaring och håller med om att modellen som Bolin och Eriksson tog fram inte duger.
Hej Pehr.
Jo att någon kan säga sig veta vad styr kilmatet och hur funktionerna kan beskrivas kräver ett självförtroende som gränsar till dumdristighet. Att klimatets parametrar och funktioner känns kaotiskt får väl ändå vägas emot att klimatet visat sig vara stabilt utan tendens att skena.
Några påtagligt enkla samband finns ju, till exempel att solinstrålning är tämligen konstant samt att jordbanan gör att vi har årstider och med årstidernas växlingar stor variation av vilka delar av klotet som tar emot instrålade energi. Att så stora förskjutningar av var inkommande energi hamnar ger upphov till svängningsfenomen visar ju havens periodiska fenomen så som el nino mm. Att djuphavs strömmar har lång svängningsperiod gör att deras verkan i tiden är svårbedömd, men att djuphavsströmmar transporterar stor mängd koldioxid mellan olika sekler är nog ganska säkert. Hur ”gammal” kan den koldioxid som uppvällande djupvatten återför till atmosfären vara?
Olaus och Michael, det är av intresse att det Murry Salby berättade om i Hamburgföredraget också presenterades vid European Geosciences Unions stora årliga konferens i Wien i april i år EGU General Assembly 2013, held 7-12 April, 2013 in Vienna, Austria.
Abstract till föredragen:
http://meetingorganizer.copernicus.org/EGU2013/EGU2013-125-1.pdf
http://meetingorganizer.copernicus.org/EGU2013/EGU2013-86.pdf
Jag har genom att se på hans senaste föredrag i Hamburg fått så pass bra grepp om hans teori om sambandet mellan koldioxidhalt och temperatur att jag tror mig ha kunnat reproducera en del av hans resultat. Om detta håller när jag jobbar vidare med det så kommer jag att ta upp det i mitt blogginlägg fredag 28 juni (på midsommarafton blir det en sommarrepris).
Ytterligare problem med hotspoten:
http://hockeyschtick.blogspot.co.uk/2013/06/new-paper-finds-hot-spot-predicted-by.html
Nu får du komma upp med något bättre än att vi just i det här fallet skall ta Lindzen på hans ord Thomas P.
Glöm inte att svara på de andra frågorna.
Pehr;
Gick tillbaka till ditt första inlägg i ämnet och sedan till din refrens Susan Solomon. Och sedan till hennes referenser. DÅ förstår man att de KAN få till en Bernkurva.
Vad ger du för detta:
http://geosci.uchicago.edu/~archer/reprints/archer.2005.fate_co2.pdf
”Both paleoclimate and computational data are consistent with a deep ocean temperature sensitivity of about 3C, which we will assume here.”
”We compromise by imposing a uniform temperature change on the waters of the ocean,”
Ooceanerna skulle alltså bli 3 grader varmare. Klart det påverkar CO2 halten i deras modeller
Samtidigt pratar de hela tiden om balansen mellan CO2 i havet och atmosfären som direkt utbyte. Och att det är havens PH som styr Revelleffekten. Men har de glömt att atmosfärens CO2 tvättas i huvudsak ut genom neutralt destillerat vatten, sk regn, varför direkta urtvättningen ur atmosfären knappast kan styras av havens temperatur.
Jo indirekt för varmare hav ger mer regn som ger större möjlighet för naturen att skrubba ur CO2 ur atmosfären.
Som vetenskapsman förstår jag att det är intressant att reda ut kurvorna. Allt talar för att Pehr har rätt. Gott så! Frågan är om dessa detaljer är viktiga? Finns liknande studier över Mars’ atmosfär? Hur intressant kolcykeln än må vara i sig, så utgår intresset ifrån att CO2 skulle ha någon avgörande effekt på jordens klimat. Bland alla de faktorer som styr jordens klimat, så är CO2 en vettlös impotent spelare. Mitt förslag är att ta ett större grep på saken och utgå från klart etablerade observationer. Här kan man trixa med kurvorna, men sådant avslöjas ganska raskt. I ett historiskt perspektiv så har det inte hänt något, som ger upphov till alarmism. Ty, så länge som de glada graderna från bronsåldern inte uppenbarar sig, så är det bara att luta sig tillbaka i soffan och fylla på rödvinsglaset med Mèdoc!
PS. tillägg till sista meningen: ”såvida inte kurvorna över temperaturen bara går ned.”
Camilla, jag håller med eller varför inte Malbec från Chile, eller Pinot Noir från Marlborough NZ, om koldioxidens från trsnporterna inte betyder något längre. Men Bordaux är ju alltid Bordaux. Trevlig sommar!
Vad visar rapporten om klyvöppningarna från dvärgbjörk från Yngre Dryas (var det väl)? CO2-halten steg snabbt till över 400ppm och sjönk sedan lika snabbt (för att det blev kallt?). Sjönk inte CO2-halten lika fort som efter bombkurvan?
Murry Salby utsätts för personangrepp men jag uppfattar honom som en mycket kompetent och seriös klimatforskare. Den avancerade lärobok i atmosfärfysik som han publicerat 1996 som jag har läst är utmärkt. Han har många välciterade vetenskapliga artiklar med atmosfärfysisk inriktning.
Det jag funnit är att Murry Salbys ekvation för att beskriva hur ändringshastigheten i koldioxidhalten beror av temperaturen stämmer mycket bra med observationer. Jag återkommer om detta med ett blogginlägg fredag om två veckor. Ekvationen, som jag kallar Salbys ekvation, är:
dy/dt = k*(T-Tb)
där y är koldioxidhalten i ppmv, k är en hastighetskonstant, T är temperaturen där man kan använda temperaturanomalerna från Hadcrutt4 till exempel och Tb är temperaturen när kolflöden till och från atmosfären är i balans så att koldioxidhalten inte ändrar sig.
Ekvationen säger alltså att koldioxidhaltens ändringshastighet är lika med noll vid temperaturen Tb och att denna ändringshastighet är proportionell mot skillnaden mellan aktuell temperatur T och temperaturen vid balans Tb.
Ungefärliga värden på de två parametrarna som jag fått fram är k = 2.5 ppmv/(C år) och
Tb = -0.4 C. När temperaturanomalin enligt Hadcrut4 är lika med -0.4 C blir alltså enligt Salbys ekvation koldioxidhalten konstant. Med Hadcrut4 lika med 0.4 C blir enligt Salbys ekvation ändringshastigheten 2 ppmv per år vilket stämmer bra med vad vi har i nuläget. När vi har en temperaturplatå skall också ändringshastigheten hålla sig konstant vilket också stämmer med observationerna.
När man integrerar Salbys ekvation över tidsperioden 1850-2012 med användning av Hadcrut4 så stämmer de beräknade värdena på koldioxidhaltens utveckling över tiden mycket bra med de observerade värdena.
Murry Salbys upptäckt av denna ekvation är alltså mycket seriös och ställer viktiga frågor som det klimatvetenskapliga samhället måste svara på och förhålla sig till.
Pehr,
Salby talar om att CO2-ökningen står i relation till ”integralen” av temperaturen snarare än bara temperaturen. Och med de siffrorna så är det ju lätt att se att det finns en sådan korrelation även då temperaturen står stilla. Men det jag undrar är vad denna ”integrala temperatur” är i fysikalisk mening. Vad refererar det till där ute, utanför matematikens värld? Och varför skulle denna integral påverka CO2?
Men kanske detta är ett ämne för ditt nästa inlägg om Salby?
Innan ”Backradiation” illusionen förvillade allmänheten såg energibalansen ut så här:
http://geo4u.edublogs.org/files/2010/04/earth_rad_budget_nasa_erbe_big.gif
Samma lite mer detaljerad:
http://cimss.ssec.wisc.edu/goes/comet/7.GIF
Notera att 19% av inkommande solstrålning absorberas i atmosfären. Att atmosfären värms med latent värme till 23% och endast med 15% av växthusgaser där H2O är viktigast. Dvs av total energiflöde till atmosfären om 64% av total inkommande solstrålning är 15% på grund av växthusgaser. Dvs atmosfären tillförs värme med hjälp av växthusgaser med endast 15/64 av total energibudget eller ca 23-24%. Lååångt ifrån Trenberts illusionstrick.
Gissa varför han var så angelägen om att införa Backradiation.
Notera också att atmosfären kyls med växthusgaser mot rymden. Hela 38/64= 60% av energibudgeten för kylning av atmosfären är beroende av växthusgaser. Just för att de blockeret direktutstrålning från jordens yta så väl
Notera också att det enda tillskott mer växthusgaser kan göra är att stänga det återstående fönstret 0m 6% av direkt utgående IR strålning. Det är omöjligt med CO2 på grund av det smala IR- spektra som CO2 har.
Notera att jag fortfarande inte talat om temperatur bara om ren energibudget. På det sätt som var brukligt fram till den av AGW förespråkarna så omhuldade ”Backradiation illusionen” tog över.
Det är helt otroligt att hela debatten om klimat och energibalansen har fått handla om CO2.
Ingemar, Salbys ekvation kan antingen anges som en differentialekvation som jag gjort ovan men man kan också integrera båda leden över en tidsperiod och då blir den totala ändringen i koldioxidhalten över tidsperioden proportionell mot integralen av skillnaden i temperatur T och temperaturen vid balans Tb.
Det är ekvationen i sin differentiella form som kan tolkas i fysikaliska termer på det sätt som jag gjorde i kommentaren ovan. Den integrala formen av ekvationen är mer praktisk att använda när man bestämmer de två parametrarnas värden med linjär regression.
Det kommer mer detaljer och resultat i mitt blogginlägg fredag om två veckor.
Pehr, kan vi få se denna ”Salbys ekvation” integrerad över en istidscykel?
Thomas, det går nog inte. Jag uppfattar själv (jag vet inte hur Salby själv tänker om detta) differentialekvationen som en avkortad Taylorutveckling av dy/dt som funktion av T runt det tillstånd där dy/dt=0 där alltså T = Tb. Ett sådant tillstånd motsvarar klimatförhållandena säg omkring år 1800 eller kanske något dessförinnan.
Det vore principiellt felaktigt att tro att en sådan Taylorutveckling skulle kunna gälla över en istidscykel under vilken det sker radikala klimatförändring av flera olika slag (Milankovich, ändringar i inlandsisar, glaciärer, havsis med motsvarande albedoförändringar etc.).
Det är märkligt hur ”grabbarna” kör ned sig i detaljerna. Frågan blir ju, om kolcykeln har någon betydelse för jordens klimat. Var finns länken? Nu vill jag ha ett svar! Ökningen av CO2 verkar ju vara inverterat exponentiell på temperaturen?
Pehr, vad sägs om senaste tusen eller kanske upp till 5000 åren? Du får själv välja rekonstruktion av temperatur och CO2 för att se om du hittar något par som passar ihop. Om du tror på någon markerad LIA eller MWP måste CO2-halten varierat radikalt under dessa.
Thomas, man kan bara spekulera om dessa saker. Hur sambandet mellan nettoändringshastigheten av koldioxidhalten i atmosfären och den globala temperaturen och andra tillståndsvariabler i klimatsystemet är antagligen beroende av klimatsystemets tillstånd. Salbys ekvation, om den verkligen visar resultatet av fysikaliska processer, gäller under en viss period där nettoändringshastigheten kan betraktas som en funktion av temperaturen plus att den gjorda linjäriseringen genom Taylorutveckling gäller.
Kanske denna ekvation skulle kunna gälla även under lilla istiden. Längre bakåt i tiden blir sannolikheten både att en annan linjärisering och att klimattillståndet har ändrats för mycket allt större vilket skulle medföra att ett annat samband skulle gälla.
Pehr, skall jag tolka det som att du tror ekvationen bara gäller under det tidsintervall för vilket kurvanpassninen skett?
Hur passar förresten denna ekvation ihop med din klimatkänslighet? Du har en rejäl positiv återkoppling mellan temperatur och CO2-halt här…
Thomas, det brukar vara så att man är försiktig med att anta att en ekvation av typen parametriseringsekvation som man har bestämt inom ett visst giltighetsområde är giltig utanför detta område. Det krävs verifiering för att utvidga giltighetssområdet om detta inte kan stödjas med teoretiska argument.
Återkoppling på grund av temperaturens inverkan på koldioxidhalten på detta sätt ligger inte till grund för gängse teorier om klimatkänslighet så det går inte att säga hur saken påverkar klimatkänsligheten.
PS Jag tror att Perfekt väntar på svar från dig 😉
Pehr, perioden för de senaste tusentalet år ligger inte utanför giltighetsområdet, om du inte räknar in tiden i denna.
Du försöker ducka för frågan om klimatkänsligheten, men om det är så att CO2-halten påverkar temperaturen, viljet du tidigare accepterat, kan du inte komma ifrån att du har en positiv återkoppling här. Bara drakdödarna som helt förnekar CO2:s effekt kommer undan.
Låt sen Perfekt vänta.
Thomas, du kan inte påstå något om giltighetsområdet för klimattillstånd där ekvationen inte är testad. Du kan heller inte veta hur klimatets tillstånd var under de senaste tusen åren. Och däri ingår hur koldioxiden varit fördelad i de olika reservoarerna.
Du försöker med ad hominemargument. Sådana är ogiltiga i sammanhanget så jag skulle egentligen inte behöva svara. Men frågeställningen är intressant.
Om vi antar att vi vet att koldioxidhalten har ökat från 280 till 390 i enlighet med Salbys ekvation och att temperaturen har stigit cirka en grad, vad blir då klimatkänsligheten? Detta skall jämföras med fallet att koldioxiden i stället steg lika mycket på grund av antropogena utsläpp med samma temperaturstegring. I det andra fallet vet vi hur vi skall beräkna klimatkänsligheten baserad på den forcing som koldioxidökningen ger tillsammans med andra kända forcings. Men hur gör vi i det första fallet?
Pehr, om ekvationen är en kurvanpassning som enbart är relevant för exakt det område i både tid, temperatur, CO2-halt, kolets fördelning etc för vilken den skapats är den totalt värdelös. Den säger i alla händelser absolut ingenting om framtida CO2-halt och eftersom det inte finns någon bakgrund till den i underliggande fysik säger den heller inget om hur klimatsystemet fungerar.
Vadå ad hominem? Är du inte lite väl känslig här?
Den beräkning av klimatkänsligheten som du försökte få publicerad tidigare, och den beräkning av Spencer du också gillat var båda helt oberoende av variationer i CO2-halten eftersom de beräknades under så kort tid. Har du nu helt förlorat tron på dessa och anser att klimatkänsligheten är helt okänd? I själva verkat spelar inte det numeriska värdet ens någon roll, systemet skenar i vilket fall som helst. Så fort temperaturen ligger över Tb kommer koldioxidhalten att stiga och driva upp temperaturen ytterligare, och i och med att du har derivatan på CO2-halten i vänsterledet finns ingen möjlighet att någonsin nå en stabil lösning.
Thomas, det finns många intressanta frågeställningar här eftersom Salbys ekvation är en ny upptäckt. Jag hinner nog inte reda ut allt i brådrasket.
Som hypotes om fysiken så menar jag att man kan ha att under den studerade tidsperioden så är nettoförändringhastigheten en funktion av temperaturen. En funktion kan Taylorutvecklas och man får då en linjär approximation som man vet har ett begränsat giltighetsområde som endast observationer kan tala om för oss hur stort det är. Både hypotesen och Taylorutvecklingen verkar stöds i detta fall av observationerna under perioden 1850 – 2012.
Hur detta kan utvidgas är en av frågeställningarna för den fortsatta forskningen. Det finns många frågor om vad klimatets tillstånd betyder och hur förändringar i detta påverkar. Saken är inte principiellt annorlunda än när man studerar andra processer som till exempel ingår i klimatmodellerna om moln, aerosoler och vattenånga till exempel.
Ditt resonemang om att återkoppling från ökad koldioxid skulle leda till instabilitet håller inte. Vattenånga är ju också en återkoppling som verkar på motsvarade sätt men leder inte till instabilitet. Bland annat beror det på det logaritmiska sambandet.
Vi kan ju också konstatera att temperaturen har legat över Tb hela tiden 1850-2012 utan att systemet skenat.
Pehr, din analogi om vattenånga håller inte. Halten vattenånga ökar med temperaturen, men når för varje given temperatur en viss jämviktsnivå. Detta är något annat än att ändringshastigheten för CO2 skulle vara proportionell mot temperaturen. Håller du temperaturen konstant på ett värde högre än Tb kommer CO2 halten fortsätta öka hur mycket som helst medan halten vattenånga snabbt stabiliseras på en något högre nivå än vid Tb.
”Vi kan ju också konstatera att temperaturen har legat över Tb hela tiden 1850-2012 utan att systemet skenat.”
För att inte tala om att den legat över Tb större delen av de föregående 2000 åren. Att systemet inte skenat säger mig att Salbys ekvation är felaktig. Det är bara en kurvanpassning som han får att passa hjälpligt under en specifik period.
Pusselbitar som passar ihop?
Bombkurvan visar att halten c14 halveras vart tionde år.
De uppgifter som finns om djuphavsströmmar är att deras
flöde är ca 600 000 km3 per år.
Koldioxidens löslighet vid nuvarande parialtryck ger att en
mängd motsvarande ca drygt en niondel av atmosfärens innehåll av koldioxid fångas
in vid djuphavsströmmarnas startområden.
Att koldioxid följer med ned när djuphavsströmmarna lämnar
havsytan behöver knappast sättas i fråga, så bomkurvan bör ju vara följden av
att koldioxidens uppehållstid i djuphavscirkulationen är uppemot tusen år.
Camilla 2013/06/15 kl 18:35 : Enligt mitt förmenande är temperaturen helt oberoende av halten koldioxid.Att denna gas med halten 0,04 % skulle vara mer bestämmande för jordens klimat än solinstrålningen är en ren gissning och inte något som man skall anpassa vår politik till. Framför allt inte slänga ut miljardernas mångfald på något så verkningslöst, som att försöka påverka temperaturen genom att minska utsläppen av koldioxid. Gissningen att det finns så kallade växthusgaser är motbevisad.Varken CO2, CH4, N2O eller vattenånga kan påverka jordens temperatur. Bara CO2 direkt ur skorstenen kan tillföra någon värme till luften. Mvh, Håkan.
Thomas,
Håller du temperaturen konstant på ett värde högre än Tb kommer CO2 halten fortsätta öka hur mycket som helst medan halten vattenånga snabbt stabiliseras på en något högre nivå än vid Tb.
Ditt resonemang är felaktigt eftersom du extrapolerar en halvempirisk modell utanför sitt observerade giltighetsområde. Redan att modellen är en avkortad Taylorutveckling innebär att linjäriteten inte kan antas bestå utanför det observerade giltighetsområdet. Exempelvis säger den övergripande kunskapen om hur koldioxid transporteras mellan reservoarerna att koldioxidhalten inte kan fortsätta att öka hur mycket som helst.
Min kurvanpassning blev för övrigt förvånansvärt bra.
Thomas, jag har funderat vidare på frågan om hur man skall uppskatta klimatkänsligheten om det skulle vara så att koldioxidökningen beror på temperaturökningen i stället för på antropogena utsläpp. Klimatkänsligheten har egentligen göra med hur jordens utgående energiflöde ändras vid en ändring av den globala temeraturen.
Ett liknande problem, men på längre tidsskala, har man när man skall uppskatta klimatkänsligheten från övergången mellan istid och mellanistid. Detta problem behandlas i följande artiklar med James Hansen som medförfattare:
Hansen och Sato (2011), Paleoclimate Implications for Human-Made Climate Change
Lorius med flera (1990), The ice-core record: climate sensitivity and future greenhouse warming,
Hansen och Sato skriver:
The fact that ice sheet and greenhouse gas boundary conditions are actually slow climate feedbacks is irrelevant for the purpose of evaluating the fast-feedback climate sensitivity (Hansen et al., 1984; Lorius et at., 1990).
Detta innebär som du kan se från Fig. 2 enligt Hansen och Sato att ändrad strålningsbalans orsakad av ändringen i koldioxidhalt betraktas som en forcing som tillsammans med andra forcings i kombination med temperaturökningen används för att beräkna klimatkänsligheten. Detta trots att ändrad koldioxidhalt har orsakats av ändrad temperatur och alltså är en återkoppling.
Om vi kan använda en analog metod i vårt fall, att ändrad strålning på grund av ändrad koldioxidhalt kan behandlas som forcing, skulle vi få samma klimatkänslighet oavsett om det är temperaturökningen eller människan som är orsaken till den ökade koldioxidhalten. Vad som behöver diskuteras vidare av forskarna är om samma metod kan användas eftersom vi talar om så pass olika tidsskalor.
Pehr,
om det finns någon sanning i Salby’s ekvation så måste den väl stämma någorlunda för t.ex. övergången från senaste istid. Åtminstone inte vara helt orimlig …
Att CO2 är integralen av temperaturen enligt den ekvation du skrivit tidigare gäller för tidsperioder upp till 100 år har jag för mig att Salby nämnde i filmen. För längre perioder måste någon begränsning komma in och ekvationen (enklast möjliga) bör då bli t.ex.
dy/dt = k*(T-Tb) – m*y
där 1/m är tidskonstanten. Om tidskonstanten är t.ex. 800 år så kan man approximera den med din tidigare ekvation (m=0) för de första 100 åren. För den nya ekvationen får man balans i för delta_y = k/m * delta_T.
Om då temperaturen höjs 5 grader vid övergång från istid till interglaciär så borde koldioxidhalten öka med t.ex. 5 * 2.5 * 800 = 10000 ppmv! Jag har tagit k = 2.5 från din skattning.
Salby’s modell ger alltså en avvikelse på en faktor 100 (100 ppmv jmf. 10000 ppmv) och även om det är stora fel i din skattning av k, min gissning av m, eller vår uppfattning av CO2- eller temperaturförändringar mellan istid och mellanistid så verkar Salby’s ekvation helt orimlig. Inte ens några försummade termer i din Taylorutveckling lär kunna rädda den, eller?
Jag ser fram mot att läsa Salby’s artikel, den borde väl publiceras snart? Någon som vet?
Pehr, jag förklarade skillnaden mellan den etablerade modellen för vattenånga och din (Salbys) modell för CO2 och varför den ena kan vara stabil medan den andra inte är det. Du kan hävda att det hela fungerar för att det tillkommer andra faktorer när man hamnar utanför denna ekvations giltighetsområde, men eftersom lösningen är instabil inom det området borde vi aldrig kunna hamna där, klimatet måste snabbt slå över åt något håll där det är mer stabilt. Som bäst är den där ekvationen oanvändbar, mer sannolikt är den helt fel.
Stig,
om det finns någon sanning i Salby’s ekvation så måste den väl stämma någorlunda för t.ex. övergången från senaste istid. Åtminstone inte vara helt orimlig …
Nej, Stig, det är inte rimligt eftersom det är fråga om helt olika tidsskalor och helt olika klimattillstånd. Om du däremot tittar på en tidsperiod på storleksordnningen hundra år under övergången från senaste istid så skulle ekvationen kunna gälla med andra parametervärden. Men detta är nog svårt att verifiera med observerade data,
Thomas, vad menar du med att ekvationens lösning inte är stabil?
Jag har löst ekvationen och lösningen var stabil under tidsintervallet 1850-2012.
Ditt påstående framstår som ogrundat.
Pehr, du kan inte testa stabiliteten på en ekvation genom att räkna baklänges och kurvanpassa på ett kort intervall. Kan du sen förklara vad denna ekvation skall vara bra för när du uppenbarligen inte själv tror att den har något att säga om verkligheten före 1850 eller efter 2012?
Thomas, jag har löst ekvationen framlänges med givna parametervärden och lösningen blev då stabil.
Poängen med Salsbys ekvation, som också gör den kontroversiell, är att den kan förklara koldioxidhalten under perioden 1850-2012 som huvudsakligen beroende av temperaturens utveckling med ett litet utrymme för antropogen ökning av koldioxidhalten.
Pehr Vad menar du med ”stabil”? Naturligtvis återfick du de värden på CO2-halten som användes för att anpassa parametrarna i det tidsintervall för vilket anpassningen skedde. Jag menar att om du har t ex en valfri, konstant temperatur som inte är exakt lika med Tb kommer koldioxidhalten sticka iväg obegränsat åt ena eller andra hållet. Har du en klimatkänslighet större än noll kommer detta påskyndas av att temperaturen också ger sig iväg åt samma håll.
Salbys ekvation ”förklarar” ingenting. Det är bara en ofysikalisk kurvanpassning. Kan du sen förklara vad denna ekvation skall vara bra för när du uppenbarligen inte själv tror att den har något att säga om verkligheten före 1850 eller efter 2012?
Pehr 18:57,
jag tror inte att klimatsystemen skiljer sig så mycket att det blir en faktor 100 fel. Det är nog svårt att rädda Salbys ekvation. Men vi får se när artikeln publiceras 🙂
Thomas,
Om man resonerar som Stig Moberg så kan ekvationen på lite längre tidsskala till exempel skrivas
dy/dt=k*(T-Tb)-m*y (korrigerad)
Detta är ett bra exempel på vad jag menar med att man inte kan gå utanför det observerade giltighetsområdet. Denna ekvation ger en stabil lösning för en konstant temperatur.
Jag vidhåller uppfattningen att Salbys ekvation är härledd från hypotesen att förändringshastigheten av koldioxidhalten är proportionell mot sagda temperaturdifferens vilket leder till att koldioxidhalten endast blir beroende av temperaturens utveckling. Om detta är giltigt så ger det inte utrymme för andra förklaringar av koldioxidhaltens utveckling utom de som ryms inom felgränserna från vad som kan beskrivas med Salbys ekvation.
Stig,
Man kan nog inte komma så långt med så enkla medel men som ett exempel kan det duga. Men tidskonstanten för atmosfären är inte 800 år. Atmosfärens tidskonstant ligger på storleksordningen 10 år.
Då ger din beräkning i stället 5*2.5*10 = 125 ppm. Detta stämmer ganska bra men är nog bara en tillfällighet.
Visst är det kul med alla friska förslag från dig och Thomas men Murry Salby är en mycket kompetent och meriterad klimatforskare så detta ger ju honom vissa plus när jag jämför er och honom. Jag har som sagt läst en avancerad lärobok i atmosfärfysik av honom som inger mycket respekt.
Pehr!
I ett inlägg i den första tråden visade jag att det ur bombprovskurvan är omöjligt att se om det finns någon revelleffekt eller inte. Gösta Petterson höll först med men gjorde sedan någon slags kovändning utan att förklara. Du kommenterade inte. I den andra tråden gjorde jag ganska sent ett inlägg men du kommenterade inte där heller.
https://www.klimatupplysningen.se/2013/05/17/klimatsimuleringar-och-observationer-strider-mot-varandra-bombprovskurvan / 2013-05-22 13:10 m.fl. inlägg
https://www.klimatupplysningen.se/2013/05/27/bombkurvan-en-gang-till/#comments 2013-05-31
Jag har tyvärr inte haft tid att analysera dina beräkningar och ändrade förutsättningar men såvitt jag förstår påverkar inte dina antaganden mitt påstående att det inte går att se någon revelleffekt. Därför postar jag min ursprungliga beräkning igen (ur inlägget 2013-05-22 13:10)
” Jag tyckte att jag var mycket tydlig. Jag försöker förklara på ett annat sätt, steg för steg.
1 Om man har en gas som är löst i en samling vatten (havet) och i luften ovanför (atmosfären) sker hela tiden ett utbyte mellan gasen i vattnet och luften Gasmolekyler lämnar spontant vattnet och går till luften och vice versa. Om vi färgar en del av luftmolekylerna röda kommer efter tillräckligt lång tid det inställt sig en jämvikt när lika många röda går till luft per tidsenhet som det går åt andra hållet. Om det finns 60 ggr fler molekyler i vattnet än i luften kommer jämvikten innebära att av 61 molekyler finns 60 i vattnet och 1 i luften. Koncentrationen i luften av de röda blir en exponentiellt avtagande funktion. Det är detta jag kallat för ’blandning’
Jag antar att du håller med så långt.
2 I fallet med bombproven tillförde man C14 men det var så lite relativt det C12 som redan fanns i atmosfären att man fick väsentligen samma avtagande kurva i atmosfären av C14 som om man samtidigt som man hade tillfört C14 hade tagit bort motsvarande antal C12. Detta eftersom blandningseffekten knappast kan ha påverkats av den lilla extra mängd C som tillförts atmosfären
Håller du med?
3 Om revelleffekten inte finns och man ökar mängden CO2 i atmosfären, a, med x molekyler så kommer den totala mängden a+x successivt minska till jämvikt uppstår med a + 1/61*x (givet att det finns 60 ggr fler C i havet). Om revelleffekten finns innebär det att övergången till havet inte blir så stor som x*60/61 C-atomer.
Håller med?
(Jag har ingen kunskap om revelleffekten men såvitt jag förstår beror den på att havet inte kan lösa mer än en del av den ökande C-mängden. Du talar om utgasning av havet. Det talar väl för att det inte går att lösa obegränsat med CO2)
4. Om ovanstående stämmer innebär det att det ur bombprovskurvan inte går att utläsa om det finns någon revelleffekt. Eftersom antalet C14, x, var litet går det inte att mäta hur det totala antalet C-atomer i atmosfären ändrades och därmed inte om det fanns någon revelleffekt. Dvs om det totala antalet atomer efter proven i luften var a + x går det inte att urskilja om det efter en tid fortfarande fanns a + x atomer kvar eller a + 1/61*x eller någonstans däremellan. I de fallen var det respektive max, ingen eller någon revelleffekt.
5 För att vara ännu mer exakt. Antag att x är så stor som 1/1000 *a (i verkligheten var den
oerhört mycket mindre). Utan revelleffekt blir antalet C14 i luft när det stabiliserat sig x /61 Med max revelleffekt skulle jämviktsläget för bomprovskurvan bli x/61 * k där k är en korrigeringskonstant som är (1 + x/a) / (1+ x/(61*a)) vilket är ungefär 1 + x/a – x/61a. Om man kunnat mäta den skulle man kunnat avgöra revelleffekten ur bombprovskurvan men det är i praktiken omöjligt även om x/a vore så stort som 1/1000 (Är någon intresserad av detaljberäkningarna kan jag posta dem).
Förstår du och håller du med om ovanstående? Om inte vore jag tacksam för ett påpekande om var jag tänkt fel eller var jag varit otydlig.”
Gösta Petterson svarade 2013/05/23 kl. 04:40:
”Det går inte att utläsa något om Revelleeffekten ur bombprovskurvan av det skäl du anger: Effekten, om den finns, är för liten för att ha någon signifikant inverkan på kurvan.”
Min kommentar:
Om det finns en Revelleffekt kan det eventuellt förklara Bernkurvan, men det går inte att utläsa om det finns någon Revelleffekt eller inte ur bombkurvan, således kan man inte säga att bombkurvan falsifierar Bernkurvan.
Pehr Björnbom 2013/06/15 kl 22:56 : Taylorutveckling påverkar inte allas att koldioxid inte påverkar klimatet ett skvatt. CO2 påverkar inte alls klimat och temperatur. Den liksom vattenånga saknar helt ”forcing” då de saknar egenskapen att vara ”växthusgaser”. Sedan är det ju av intresse att finna samband mellan den styrande temperaturen och halten CO2″ i luften, men klimatet påverkas ju inte. Mvh, Håkan.
Nils G, tack för en intressant kommentar. Men den var mycket lång och i stället för att gå in på detaljfrågorna så skall jag försöka svara på huvudpunkten, nämligen hur Revelleeffekten kan synliggöras i bombprovskurvan.
Först, vad är Revelleeffekten? Idén med Revelleeffekten är att när koldioxid löses upp i en vattenlösning av karbonater (som havsvattnet är förutom saltinnehållet) så minskar dess pH. Ju lägre pH desto mindre mängd koldioxid kan lösa sig från luften. Om koldioxiden skulle vara i jämvikt mellan hav och luft så innebär en pH- minskning att koldioxid lämnar havet och tillförs luften, luftens koldioxidhalt ökar. Det senare kan hända med 14C-koldioxid om man tillför fossil koldioxid till havet. Det var detta som Bolin och Eriksson (1959) visade.
För att få grepp om denna effekt så måste man använda matematisk analys och det är resultatet av en sådan som jag visar i ovanstående blogginlägg. Om vi inte har någon Revelleffekt, R=1, så blir kurvan enligt Bolins och Erikssons modell en kurva med nära nog exponentiellt avtagande mängd av 14C i atmosfären. Men när vi har med Revelleeffekten på de olika nivåerna R=2-12.5, där den högsta nivån var vad Bolin och Eriksson antog borde vara den som gäller, så blir kurvformen starkt deformerad med början på slutet av 1980-talet. Anledningen till detta är alltså att under de drygt fyrtio år som kurvan omfattar har koldioxidhalten i luften ökat med omkring 70 ppmv vilket enligt Bolins och Erikssons teori har minskat pH i framförallt det omblandade skiktet av havet.
Lägg märke till att Revelleeffekten innebär att mängden 14C-koldioxid i atmosfären, i och med den fortsatta ökningen av koldioxidhalten i atmosfären, går genom ett minimum för att börja öka. Enligt mina beräkningar skulle denna ökning redan ha skett i mer än tio år för av Bolin och Eriksson antagna nivåer på Revelleeffekten. Havet skulle alltså i dag enligt mina beräkningar var en källa för 14C-koldioxid, inte en sänka.
Från kolcykellitteraturen kan man se att forskarna är medvetna om att denna övergång från sänka till källa bör ske. I följande artikel
Levin, I., Naegler, T., Kromer, E., Diehl, M., Francey, R. J., Gomez-Pelaez, A.J., Schäfer, A., Steele, L. P., Wagenbach, D., Weller, R., and Worthy, D. E. 2010. Observations and modelling of the global distribution and long-term trend of atmospheric 14CO2. Tellus 62B, 26-46, DOI: 10.1111/j.1600-0889.2009.00446.x.
skriver man:
The ocean–atmosphere disequilibrium today is close to pre-industrial times, but, due to increasing fossil fuel CO2 emissions, the ocean will most probably be turning from a sink of radiocarbon (natural but also anthropogenic) to a source over the next decade. This is considerably earlier than predicted by Caldeira et al. (1998).
Det märkliga är att man i denna artikel med många referenser inte nämner Revelleeffekten och inte citerar vare sig Revelles klassiska artikel eller Bolins och Erikssons klassiska artikel om denna effekt. Men i citatet säger man att oceanen på grund av våra fossila koldioxidutsläpp kan förväntas övergå från att vara en sänka för 14C-koldioxid till att bli en källa. Men detta har uppenbarligen ännu inte skett utan förväntas ske först under innevarande decennium enligt författarna men ännu senare enligt en av dem citerad artikel.
Det verkar alltså att den förväntade Revelleeffekten dröjer. Har vi månne även här ett pausfenomen, dvs. att Revelleeffekten har tagit en paus ungefär som temperaturstegringen?
Håkan, att du och jag har olika uppfattnngar om koldioxidens roll som växthusgas har vi väl redan ältat ad nauseam.
Pehr, vad anser du om Mats Almgrens inlägg på UI där han bl a visar på en kurva över mängd C-14 i atmosfären som stiger precis som förutsagt enligt Revelleffekten?
Thomas, uppenbarligen överensstämmer denna kurva som den tolkas av Mats Almgren inte med vad Levin och medförfattare (2010) eller Caldeira (1998) skriver. Detta kan antingen bero på Mats Almgren tolkar kurvan fel eller på att forskarna inom området har olika uppfattning om saken.
Jag tänkte denna artikel kunde intressera herrarna:
http://reef01.marine.usf.edu/sites/default/files/project/cariaco/publications/Astor_et_al_2013.pdf
Havet utanför Venezuela är en CO2-nettokälla utom vid kraftiga uppvällningar.
Perfekt!
Äntöigen en fältstudie av samband mellan havstemp och co2 nivåer! Som tillbehör till bombkurva och Salby och bernmodeöllen är detta vad som saknas i ett ströre sammanhang. OBSERVATIONER!!
Pehr, Levin skriver också ”Dedicated simulations of global trends and interhemispheric differences with respect to atmospheric CO2 as well as δ13CO2 and 14CO2, are shown to be in good agreement with the available observations (1940–2008).” Hur går det ihop med din tes om att kolmodellerna är helt fel?
Sen trodde jag konsensus på denna blogg var att observationer övertrumfade modeller, så varför hänvisa till en modell som Levins för att hävda att observationer är fel?
Thomas, någon tes om att modellerna är helt fel driver jag inte. När det gäller vikten av observationer så brukar man väl ofta citera Richard Feynman:
In general we look for a new law by the following process. First we guess it. Then we compute the consequences of the guess to see what would be implied if this law that we guessed is right. Then we compare the result of the computation to nature, with experiment or experience, compare it directly with observation, to see if it works. If it disagrees with experiment it is wrong. In that simple statement is the key to science. It does not make any difference how beautiful your guess is. It does not make any difference how smart you are, who made the guess, or what his name is – if it disagrees with experiment it is wrong. That is all there is to it.
Pehr Björnbom 2013/06/18 kl18:25 Du citerar Feynman : ” If it disagrees with experiments it is wrong” Här har vi ett ”experiment, som har pågått i över 16 år. Vi har släppt ut mängder av koldioxid och temperaturen har inte ökat. Detta visar att hypotesen eller rättare sagt gissningen att koldioxid påverkar klimat och temperatur är helt uppåt väggarna fel. It is wrong! Även om detta är äcklande. Mvh, Håkan.
Håkan, jo, men detta strider inte mot att koldioxiden är en växthusgas eftersom det kan bland annat förklaras med att återkopplingarna inte fungerar som teorin antar.
Pehr Björnbom 65 : Men varför skulle just DEN teorin fungera i det här sammanhanget? Mvh, Håkan.
Pehr 2013/06/18 kl. 12:54, #56
Tack för svar. Jag har tyvärr ont om tid så jag har inte haft möjlighet att läsa Bolin o Erikssons artikel och bara skummat din fördjupningsrapport. Att bombkurvan vänder lite uppåt på slutet beroende på att man tillför antropogen CO2 verkar rimligt och det har man tydligen också observerat och att detta även påverkas av revelleffekten verkar också rimligt. Frågan är dock om det är detta du avser när du i inledningen av tråden säger ” En del anser att kurvorna faktiskt skall vara så olika som de är medan andra, inklusive jag själv, anser att bombkurvan och Bernkurvan borde likna varandra mera och att Bernmodellen alltså falsifieras av olikheten.” Det vore obegripligt.
Visst kan du diskutera utseendet av svansen på kurvan, men eftersom du så starkt betonar påståendet ovan och dessutom i första meningen säger att Gösta Petterssons analys av bombkurvan är ”eminent” borde väl det vara bra att även försvara den åsikten mot min kritik. Så långt var inte mitt inlägg. Du visar ju även att du fullt ut förstår att Bernkurvan och bombkurvan beskriver två helt olika fenomen. Bernkurvan visar hur fort och hur mycket ett överskott av C i atmosfären går till havet eller andra sänkor. Bombkurva visar hur fort ett visst slags atomer, C14, blandas ut med andra C-atomer. Det är långt ifrån självklart att dessa två fenomen skulle likna varandra.
Nils G, tack för ett intressant och tankeväckande svar!
Först vill jag påpeka att mitt blogginlägg härovan svarar på den första punkten du tog upp i din tidigare kommentar som numera har nummer 54:
I ett inlägg i den första tråden visade jag att det ur bombprovskurvan är omöjligt att se om det finns någon revelleffekt eller inte.
Den analys som jag gjort med hjälp av Bolins och Erikssons matematiska modell visar däremot otvetydigt att det ur bombprovskurvan borde vara fullt möjligt att se om det finns en Revelleeffekt eller inte. Detta beror på att Revelleeffekten, som orsakas av de antropogena utsläppen av fossil koldioxid, påverkar fördelningen av radioaktiv koldioxid mellan luft och hav och hastigheten i överföringen mellan luft och hav. Detta leder till att bombkurvan deformeras som visas i det andra diagrammet ovan.
När jag talar om att det borde finnas en likhet mellan bombkurvan och Bernkurvan så är det detta uttryck för Revelleeffekten jag syftar på. Bernkurvan ger klart uttryck för Revelleeffekten. Bombkurvan behöver inte vara helt lik Bernkurvan men den borde i likhet med Bernkurvan ge uttryck för Revelleeffekten. Om bombkurvan, inklusive svansen efter den, inte gör detta så menar jag att den falsifierar Bernkurvan.
Vad jag dessutom finner märkligt är att i de artiklar från kolcykellitteraturen som jag läst är det så tyst om Revelleeffekten i samband med bombkurvan. En reviewartikel av Levin och Hesshaimer (2000) diskuterar utförligt bombkurvan och dess betydelse för kolcykelforskningen men jag kan inte finna minsta referens till Revelleeffekten. De klassiska artiklarna av Bolin och Eriksson (1959) och Revelle med flera (1957) är inte citerade. Däremot diskuterar man Süesseffekten och citerar Süess (1955). Varför är man så tyst om Revelleeffekten?
Tack för svar!
Jag har alltså uppfattat dig rätt att du anser att likheterna mellan bombkurvan och bernkurvan är att bombkurvan i din variant med en uppåtböj i slutet är lik bernkurvan eftersom båda är påverkad av revelleffekten. Nu är det dock inte vad du säger i början av inlägget och inte heller vad Gösta Pettersson sa i den inledande bombkurvstråden. ” En del anser att kurvorna faktiskt skall vara så olika som de är medan andra, inklusive jag själv, anser att bombkurvan och Bernkurvan borde likna varandra mera och att Bernmodellen alltså falsifieras av olikheten.” I det här citatet refererar du till fig 3 ovanför och där finns ingen uppåtböjd svans på bombkurvan. Vem skulle kunna tolka ditt uttalande i citatet som att du saknar den böjda svansen och kurvorna då skulle bli mer lika. Du (och Gösta) hävdade dessutom i den första tråden just det du sade i citatet ovan och då hade du inte börjat tala om svansen.
Varför säger du inte som det är, som du vet och även en AGW-kritisk debattör sa i den första tråden att det är uppenbart att Gösta Petterson hade fel i hur bombkurvan falsifierar bernkurvan? Jag tycker faktiskt att du borde börja en ny tråd där du tydligt förklarar just detta. Jag gissar att det inte är så många som följer kommentarerna nu på den här tråden. Eller är det emot bloggens policy att erkänna att en skeptiker kan ha fel.
Jag har några funderingar kring hur stor uppåtsvansen verkligen kan vara men jag har inte tänkt färdigt om det och får återkomma. Levin och Hesshaimer (2000) har jag inte läst och har inga kommentarer.
#69 Nils G: ”[…] Jag gissar att det inte är så många som följer kommentarerna nu på den här tråden.[…]”
– Jodå. 🙂
Nils G, tack själv för svar! Det verkar som vi har kunnat stämma av våra åsikter korrekt mot varandra.
Jag anser dock att Gösta Petterssons kritik inte är tillbakavisad. Kurvan i figur 3 uppfattar jag att den motsvarar den kurva i figur 2b i Levin och Hesshaimer (2000) som markerats med en pil och ordet Troposphere. I GPs figur 3 har denna kurva ritats om med exponentialkurvans nollasymptot om nollinje.
Om jag har uppfattat detta rätt varför är denna kurva en exponentialfunktion? Varför är den inte deformerad av Revelleeffekten på det sätt som visas i min andra figur i blogginlägget ovan?
Det är mycket som inte stämmer här, tycker åtminstone jag.
Pehr ” Varför är den inte deformerad av Revelleeffekten på det sätt som visas i min andra figur i blogginlägget ovan?”
Om jag förstår det rätt visar din andra figur på absoluta mängden C-14 medan Levins figur visar på relativa andelen C-14. Som framgår av den tidigare nämnda kurvan från Wellington ser man att mängden börjar öka efter sekelskiftet.
Thomas,
Den figur jag avsåg är figur 2b i Levin och Hesshaimer (2000) vars motsvarighet jag uppfattar att Gösta Pettersson har representerat i procentuell form i sin figur 3 där nollinjen motsvarar den exponentiella kurvans nollasymptot.
Levins och Hesshaimers figur 2b har mängden radioaktiv koldioxid på y-axeln, närmare bestämt uttryckt i antalet radioaktiva kolatomer. Kurvan för troposfären är en omräkning av kurvan i figur 2a som däremot visar en form av relativ andel som vanligtvis används när man vill ge ett mått på halten av ett radioaktivt spårämne.
Pehr, du har rätt i att den mätte mängd, jag tittade för hastigt bara på 2a, men jämför du med Wellingtonkurvan vänder den som sagt inte uppåt förrän efter sekelskiftet vilket inte skulle synas här.
Thomas, som jag skrev i kommentar # 59 ovan så stämmer inte en sådan tolkning av Wellingtonkurvan med vad Levin och medförfattare (2010) eller Caldeira och medförfattare (1998) skriver om tidpunkten för när havet skall övergå från sänka till källa för radioaktiv koldioxid.
Man måste kanske ta hänsyn till att det finns en viss standarddeviation i värdena som man måste ta hänsyn till när man tolkar Wellingtonkurvan. Jämför Gösta Petterssons figur 3 ovan där jag antar att punkterna representerar medelvärden för de olika mätstationerna medan Wellingtonkurvan representerar just bara Wellington.
Pehr, som konstaterades på UI varierar den naturliga tillförseln av C-14 en del, och sen modellerna inte perfekta vilket båda gör att man inte kan exakt kan försutspå när minimum skall inträffa. Även Levin konstaterar att hans modell inte helt överensstämmer med Caldeira. Vad jag förstår tror du dessutom varken på Caldeiras eller Levins artiklar så det är lite lustigt hur du framhåller dem som auktoriteter.
Vad som står helt klart är i alla fall att det ursprungliga påståendet att avklingningen av C-14 i atmosfären skulle ge livslängden för CO2 är fel.
Thomas, jag försöker bara något sånär synliggöra var gränserna för vårt vetande om vad som händer med koldioxiden går.
Ingeborg Levins och hennes medarbetares kolcykelmodell är dels komplicerad, dels skiljer den sig förmodligen som du säger från Caldeiras med fleras. Dessa modeller är underkastade komplexitetsparadoxen precis som klimatmodellerna så det kommer alltid att finnas tolkningsosäkerheter av olika slag.
Jag vet inte exakt vad det betyder att Levin med flera säger att havet övergår från sänka till källa i framtiden, om så och så många år. Men troligen betyder det åtminstone att detta ännu inte skett. Vad man säger i artikeln om Wellingtonkurvan som UI citerar vet jag inte då den är bakom betalvägg men i abstract sägs ingenting om att någon sådant övergång från sänka till källa skulle ha skett. Därför gissar jag på att Wellingtonkurvan faktiskt inte visar detta utan att detta är en feltolkning av den som läst artikeln.
Vad betyder det Levin och Caldeira med flera säger för Revelleeffekten? Det är svårt att säga eftersom detta beror på hur deras modeller är konstruerade. Om Revelleeffekten vore förutbestämd på det sätt som i Bolins och Erikssons modell så kan naturligtvis modellutfallet inte säga något om detta. Men jag kan tänka mig att modellerna inte har en bestämd Revelleeffekt på detta sätt utan att modellutfallet faktiskt ger information. Det skulle vara intressant att få veta från forskare som utvecklar och använder dessa modeller vad de säger om just denna fråga. Jag är förvånad att dessa artiklar inte diskuterar Revelleeffekten.
Det är för övrigt helt klart att den radioaktiva koldioxidens avklingning kan användas för att bestämma tidskonstanter i till exempel Bernmodellen. Läs Bolin och Eriksson (1959) så ser du att det är så. Men det finns även andra metoder och kritiken är att det finns motsägelser i de värden som redovisas för Bernmodellen jämfört med bombkurvan. Detta är vad som sagts och där finns inget fel enligt min mening.
Pehr Björnbom # 77 : Är det inte dags att försöka få en kompetent fysiker att titta på ”bombkurvan” med tillbehör? Själv är jag helt ointresserad, då jag anser att klimatet år oberoende av halten koldioxid i luften. Jag anser ju tveklöst, att ifrågavarande gas inte är en så kallad ”växthusgas”. Mvh, Håkan.
Pehr Björnbom 2013/06/21 kl. 14:31
Men Pehr, har du läst vad Gösta Petterson egentligen skriver? I sin sjusidiga rapport som refereras till i den första tråden om bombkurvan gör Gösta Petterson väsentligen två påståenden. Det första är
”Det är fullt befogat att beskriva relaxationen av atmosfäriska överskott av koldioxid som en monofasisk exponentiell process styrd av en enda relaxationstid, dvs. att karakterisera den med en konventionellt tolkad uppehållstid.” Alltså en enda exponentiell process.
Det andra är:
”Bernmodellen (blå kurva i Fig. 3) ger en acceptabel beskrivning av de första 2–3 årens minskning av överskottet av C14-koldioxid. Därefter saknas varje som helst överensstämmelse mellan den empiriska bombprovskurvan och Bernmodellens beskrivning av relaxationsförloppet. Modellen ger en gravt överdriven bild av hur länge ett överskott av koldioxid stannar kvar i atmosfären. Bernmodellen (blå kurva i Fig. 3) ger en acceptabel beskrivning av de första 2–3 årens minskning av överskottet av C14-koldioxid. Därefter saknas varje som helst överensstämmelse mellan den empiriska bombprovskurvan och Bernmodellens beskrivning av relaxationsförloppet. Modellen ger en gravt överdriven bild av hur länge ett överskott av koldioxid stannar kvar i atmosfären.”
Han hävdar alltså att bernkurvan och bombkurvan borde överensstämma inte bara de första 2-3 åren utan även de följande tjugo åren. Det stämmer inte med vad du påstår! År inte detta uppenbart? Han påstår just det ovanstående och inget annat! Ändå påstår du att han inlägg är ”eminent”. Det är just detta jag invänder emot.
(Vad som händer senare i bombkurvan är en annan fråga)