Vi välkomnar Gösta tillbaka till KU, efter en tids bortvaro
Gästinlägg #8 av Gösta Pettersson
I ett KU-inlägg med titeln ”Revellefaktorn, lika viktig som klimatkänsligheten” har Pehr Björnbom påpekat att samtliga IPCC-stödda klimatmodeller baserar sig på kolcykelmodeller som utgår från att oceanernas förmåga att ta upp antropogena koldioxidutsläpp starkt begränsas av den så kallade Revelleeffekten. Denna anses uppkomma genom utsläppens inverkan på havets karbonatkemi och karakteriseras kvantitativt av en konstant kallad Revellefaktorn.
Den termiska luft/hav-modell jag beskrivit i tidigare KU-inlägg kritiserades av vissa kommentatorer som påpekade att jag inte tagit hänsyn till Revelleeffekten. I detta inlägg ska jag förklara vad denna brist på hänsynstagande grundar sig på genom att redovisa min syn på de två arbeten som en gång i tiden introducerade Revellefaktorn och enligt mångas åsikt lade grunden för klimatalarmismen.
Henrys lag säger att jämviktstrycket av en gas ovanför en vätskefas är proportionellt mot gasens koncentration i vätskan. Partialtrycket (p) av koldioxid i luften är alltså vid jämvikt proportionellt mot havets koldioxidhalt, och därmed mot havets totala halt (y) av karbonatföreningar (koldioxid, kolsyra, bikarbonat- och karbonatjoner). Det innebär att ändringar (∆p) av koldioxidens partialtryck vid konstant pH och temperatur måste ge upphov till proportionella ändringar (∆y) av havets jämviktshalt av karbonatföreningar enligt sambandet
∆p/p = ∆y/y (1)
I ett för klimatologer klassiskt arbete år 1957 fann Revelle och Suess att antropogena utsläpp inte kan vara den huvudsakliga orsaken till att luftens koldixidhalt ökat om Ekv. (1) gäller, men skulle kunna vara det om ökningar av p leder till cirka 10 gånger mindre ökning av y än vad Ekv. (1) föreskriver. De föreslog därför att överföringen av luftöverskott av koldioxid till havet styrs av sambandet
∆p/p = R (∆y/y) (2)
där den så kallade Revellefaktorn R betraktades som en konstant med ett värde nära 10. Införandet av denna faktor minskar formelmässigt vattnets förmåga att ta upp luftkoldioxid med en faktor 10. Det innebär att antropogena koldioxidutsläpp modellmässigt stannar kvar i luften avsevärt längre och i långt högre grad än vad man har anledning förmoda på grundval av empiriskt bestämda data för koldioxidens atmosfäriska uppehållstid och förmodade förindustriella jämviktsfördelning mellan luft och hav.
Som motivering för införandet av faktorn R ≈ 10 anförde Revelle-Suess ”vattnets speciella buffertmekanism”. Vad klimatologer omsider kom att förstå med detta klargjordes året efter av Bolin och Eriksson i ett arbete där de påpekade att upptag av koldioxid i rent vatten försurar detta. Genom att granska effekten av försurningen på proportionerna mellan olika karbonatföreningars halter ansåg sig de senare författarna kunna fastställa att Revellefaktorns värde är 12.5.
Nu är det så att Henrys lag har fått namnet ”lag” eftersom dess giltighet är utomordentligt väl befäst. Teoretiskt kan den härledas från grundläggande termodynamiska samband, t. ex. från massverkans lag. Experimentellt har den för koldioxidens del befunnits gälla för temperaturer upp till 100 ˚C och för tryck från bråkdelar av en atmosfär till 1000 atmosfärer. Revelle och Suess presenterade Ekv. (2) som ett jämviktssamband gällande havet i sin helhet och vid konstant pH. Därför kan man direkt konstatera att deras förslag att R ≈ 10 strider mot Henrys lag, vilken föreskriver att R = 1 vid jämvikt under de angivna förhållandena.
Bolin och Eriksson tycks ha varit medvetna om detta, eftersom de betecknade Ekv. (2) som ett apparent jämviktsamband gällande enbart för upptaget av luftöverskott av koldioxid i oceanernas ytvatten. En grundförutsättning i deras resonemang var nämligen att luftens koldioxid befinner sig i omedelbar jämvikt med ytvattnets karbonatföreningar. Dessutom vände de sig mot Revelle-Suess förmodan att Ekv. (2) gäller vid konstant pH genom att tvärtom hänföra Revelleeffekten till den försurning av havet som utsläppen av antropogen koldioxid antogs ge upphov till.
Bolin-Erikssons slutsatser har rönt stark kritik från forskare som haft en annan syn på om, och i så fall hur mycket, koldioxidutsläpp försurar havet. Min egen främsta invändning mot slutsatserna är de dragits på teoretiskt osunda grunder, vilket lett till en felaktig tillämpning av Ekv. (2).
Matematiskt kan detta belysas genom att notera att variabeländringarna ∆p och ∆y förutsätts uppstå på grund av kontinuerliga utsläpp av antropogen koldioxidutsläpp. Det innebär att variablerna p och y varierar med tiden t. Beaktar man detta tidsberoende, och övergår till mera allmängiltiga infinitesimala storheter, så står Ekv. (2) i själva verket för sambandet
(dp/dt) / p = R [(dy/dt) / y] (3)
Bolin-Erikssons grundförutsättning att luftens koldoxid alltid befinner sig i jämvikt med ytvattnets karbonatföreningar innebär att man förutsätter att dp/dt = dy/dt = 0 enligt definitionen av jämvikt. Deras på denna förutsättning baserade analys av ytvattnets karbonatkemi kan därför omöjligen leda till slutsatsen att R = 12.5. Jämviktsförutsättningen reducerar nämligen Ekv. (3) till 0 = R*0, vilken inte kan lösas med avseende på R. Det går inte att fastställa något värde på R med Bolin-Erikssons analytiska tillvägagångssätt under de av dem angivna förutsättningarna.
Man kan inte både ha kakan och äta den. Man kan inte karakterisera den tidsberoende variationen av luftens koldioxidhalt (ändringarna ∆p) genom analyser som samtidigt förutsätter att det inte föreligger någon tidsberoende variation. Som kinetiker inser jag att Bolin-Eriksson försökt använda sig av en tidshierarkisk jämviktsapproximation. Men de har infört den på ett oprofessionellt sätt som står i strid med elementär kinetisk teori och har lett till en felsyn på vad som hastighetsbegränsar havets upptag av luftöverskott av koldioxid. Jag ska strax återkomma till detta.
Utsläpp av antropogen koldioxid stör rådande förhållanden och startar eller vidmakthåller relaxationsprocesser som strävar mot att åstadkomma jämvikt i systemet. Det vi vanligen uppfattar som naturens upptag av utsläppen är kinetiskt sett relaxationen (jämviktsinställningen) av ett system som inte är i jämvikt. Sådana systems beteende uppvisar ett tidsberoende som kinetiker normalt försöker beskriva med modeller som utgår från de beaktade variablernas tidsderivator. Det finns ingen som helst anledning att tro att icke-jämviktssystems generella beteende kan beskrivas med tidsoberoende jämviktssamband som Ekv. (2), inte ens om sambanden kallas apparenta.
Tag det enkla fallet att en utsläppspuls höjer koldioxidens lufthalt med ∆p. Vid utsläppstillfället (tiden t = 0) är havshalten av karbonatföreningar oförändrad, dvs. ∆y = 0. Enligt Ekv. (2) är alltså Revellefaktorn initialt oändligt stor. Den antar inte ändliga värden förrän relaxations-processen kommit igång, så att ∆y gradvis ökar och ∆p gradvis minskar genom koldioxid-överföring från luften till havet. Det belyser att storheten R i Ekv. (2) [eller i den matematiskt korrektare Ekv. (3)] inte är någon reaktionskarakteristisk konstant. R är en tidsberoende funktion, så snart man låter x stå för luftens tidsberoende koldioxidhalt och y för den tidsberoende halten av karbonatföreningar i havet.
I det komplexare fallet med kontinuerliga koldioxidutsläpp kommer storleken av R fortfarande att variera med tiden och att bero av utsläppstakten, dvs. bestämmas av hur stora de årliga utsläppen varit och hur utsläppsmängderna förändrats under industriell tid. Ändras havstemperaturen under processens gång, så kommer även detta att påverka värdet av R.
Därför är det helt obefogat att grunda analyser av tidsberoendet av havets upptag av luftöverskott av koldioxid på Ekv. (2) och på förmodandet att Revellefaktorn har ett fixt värde. Nytänkande i all ära, men relaxationskinetisk teori har sedan länge gett välbefogade anvisningar om hur sådana analyser ska genomföras vad boxmodeller beträffar: Man preciserar och löser de differentialekvationer som beskriver tidsberoendet av beaktade variabler. Det var den metod Revelle & Suess (1957) använde sig av fram till den osunda introduktionen av Revellefaktorn. Det var likaså den metod jag använde mig av när jag utvidgade den sunt härledda delen av deras luft/hav-modell genom att även ta hänsyn till temperaturberoendet av koldioxidens vattenlöslighet (False Alarm, Paper 4).
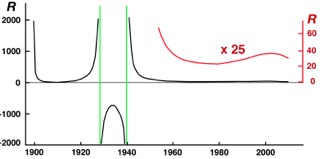
Det dyker alltså aldrig upp någon Revellefaktor vid en strikt matematisk lösning av de kinetiska differentialekvationerna för Revelle-Suess luft/hav-modell. Det är den enkla förklaringen till att jag ”försummat” att ge Revellefaktorn något värde vid härledningen av den termiska luft/hav-modellen. Däremot kan man enkelt avgöra hur funktionen R (så som den definieras av Ekv. 3) enligt modellen har varierat under industriell tid. Fig. 1 nedan visar resultaten av sådana beräkningar för perioden 1900–2012.
Figur 1. Revellefaktorns variation 1900-2012 enligt den termiska luft/hav-modellen,
beräknad för uppehållstiden 14 år och aktiveringsenergin 165 kJ/mol/K
Figuren illustrerar att det beräknade variationsintervallet för R faktiskt sträckt sig från -∞ till +∞ under 1900-talet. Det hänger samman med att dy/dt enligt modellen bytte tecken under 1930-talets värmeperiod, då havet på grund av termisk avgasning temporärt avgav mer koldioxid än det tog upp från luften. Det temporära teckenbytet medför att dy/dt två gånger antagit värdet 0 och därmed gett upphov till de två singulariteter som anges av de lodräta gröna linjerna i figuren; R bestäms enligt Ekv. (3) av ett uttryck där dy/dt står i nämnaren och antar därför obegränsat stora eller små värden när dy/dt går mot noll.
Singulariteterna kan måhända ses som kuriosa. Men figuren belyser med all önskvärd tydlighet att Revellefaktorn R är en tidsberoende funktion, vars värde kan förväntas uppvisa stora variationer. Det gäller även för tidsperioder där inga singulariteter uppträder. 1950–2012 har R enligt modellen varierat tämligen oregelbundet mellan ungefär 20 och 100 (röd förstoring i figuren) som svar på de oregelbundna jämviktsstörningar som koldioxidutsläpp och temperaturvariationer åstadkommit.
Att R skulle uppvisa ett konstant värde nära 10 under hela den industriella eran är en befängd tanke som saknar något som helst stöd i relaxationskinetisk teori.
Då kan vi återgå till att granska det jämviktsresonemang som fött tanken på Revellefaktorns konstans och deskriptiva användbarhet.
Vid relaxationskinetiska analyser introducerar man ofta approximationer som grundar sig på en tidshierarkisk uppdelning av processerna. Är man huvudsakligen intresserad av vad som sker på decennienivå, då kan man tillåta sig att helt bortse från reaktionssteg som är så långsamma att de kräver tusentals år för att ge signifikanta effekter. Analogt kan man särbehandla mycket snabba reaktionssteg med en approximation som innebär att reaktanterna i de snabba stegen alltid antas befinna sig i jämvikt med varann.
Därför är det inget som helst fel på Bolin-Erikssons förutsättning att luftens koldioxid jämviktar snabbt med havets ytvatten. Tvärtom är det i det närmaste en självklarhet att så måste vara fallet över de tidsskalor (år till millennier) som normalt beaktas i diskussionerna av koldioxidutsläppens effekter. Laboratoriemässigt inställer sig koldioxidens luft/vatten-jämvikt nära nog fullständigt inom loppet av några sekunder. Det betyder att något helt annat än hydratiseringssteget begränsar farten av havsupptaget av koldioxidutsläpp. Bolin-Erikssons jämviktsförutsättning stöds dessutom av experimentella ytvattenobservationer (Sundquist et al., 1979).
Ur teoretisk aspekt är det alltså fullt befogat att införa en tidshierarkisk jämviktsapproximation på basis av förutsättningen att luftens koldioxid jämviktar snabbt med havets ytvatten. Men då måste man också beakta vad kinetisk teori föreskriver om approximationens innebörd och konsekvenser. Den för bland annat med sig att man inte längre kan särskilja luften och ytvattnet som två kinetiskt separata boxar. I stället måste de matematiskt behandlas som en enda box, där ytvattnet kan ses som en förlängning av atmosfären (se t. ex. ovannämnda artikel av Sundquist et al.).
Inom denna box styrs enligt jämviktsapproximationen kolets fördelning mellan luft och ytvatten av Henrys lag. Ytvattnets halt av karbonatföreningar är alltså i varje ögonblick proportionell mot luftens koldioxidhalt. Proportionalitetskonstanten avgör hur stor del av den totala mängden kol i boxen man återfinner i luften respektive i ytvattnet. Den avgör därmed också storleken av den del av ett koldioxidutsläpp som omedelbart tas upp i ytvattnet, dvs. tas upp i havet utan tidsfördröjning.
Men vad man genom jämviktsberäkningar kommer fram till beträffande ytvattnet kan absolut inte extrapoleras till att även gälla havet under ytvattnet, i fortsättningen kallat egentliga havet. Henrys lag gäller endast vid jämvikt. Den kan inte användas för att fastställa relationen mellan luftens halt av koldioxid och halten karbonatföreningar i det egentliga havet, eftersom koldioxidutbytet mellan luft och det egentliga havet befinner sig fjärran från jämvikt. Det egentliga havets halt av karbonatföreningar är inte proportionellt mot luftens koldioxidhalt, utan relationen mellan de senare två variablerna bestäms av dessas kinetiska differentialekvationer.
Med hänvisning till Bolin-Erikssons arbete har ett otal klimatforskare och andra debattörer hävdat att antropogena koldioxidutsläpp på grund av Revelleeffekten leder till en successiv försämring av havets förmåga att ta upp koldioxid. Det är en missuppfattning som grundar sig på att man i likhet med Bolin-Eriksson inte förmått särskilja mellan vad som gäller för ytvattnet respektive för det egentliga havet. Det är möjligt att ökningen av luftens koldioxidnivåer har lett till en försurning av ytvattnet enligt de jämviktssamband som utretts av Bolin-Eriksson. Detta har i så fall försämrat ytvattnets förmåga att ta upp koldioxid och minskat den andel av luftburna koldioxidöverskott som lösts i ytvattnet utan tidsfördröjning.
Men ytvattnets speciella egenskaper säger ingenting om hur snabbt luftöverskott av koldioxid tas upp i det egentliga havet. En tidshierarkisk jämviktsapproximation baserad på Bolin-Erikssons jämviktsförutsättning medför nämligen att uppmätta uppehållstider för luftens koldioxid tekniskt sett kommer att svara mot koldioxidens transport från atmosfär/ytvatten-boxen direkt till det egentliga havet. Ytvattnet blir ett gränsskikt utan hastighetsbegränsande betydelse.
För att förtydliga innebörden av detta kan jag erinra om att Bolin-Eriksson betecknade ytvattnet som en flaskhals för havets upptag av luftburen koldioxid. Med deras jämviktsförutsättning hamnar emellertid ytvattnet kinetiskt sett så fjärran från en flaskhals man kan komma; koldioxiden förutsätts ju tagas upp oändligt snabbt. Den verkliga flaskhalsen, det som kinetiker brukar kalla processens hastighetsbegränsande steg, utgörs i stället av karbonatföreningarnas transport från ytvattnet till det egentliga havet. Det är detta steg som ger upphov till tidsberoendet av koldioxidupptaget och som fartmässigt svarar mot de experimentellt uppmätta uppehållstiderna för atmosfärisk koldioxid.
Bolin-Erikssons jämviktsförutsättning medför alltså definitionsmässigt att ytvattnet inte bidrar till hastighetsbegränsningen av koldioxidtransporten från luft till hav. Det innebär att ytvattnets karbonatkemi saknar betydelse för tolkningen av koldioxidens experimentellt uppmätta uppehållstid. Jämviktsfördelningen av kol mellan luft och ytvatten bestämmer endast storleken av den del av en utsläppspuls av koldioxid som går direkt ner i vattnet utan tidsfördröjning. Den delen är enligt bomb-C14-inventeringarna försumbart liten. Detta torde först och främst återspegla att ytvattnet utgör en försumbart liten del av den totala havsvolymen, men även försurning av ytvattnet kan vara en delförklaring.
Oavsett varför den omedelbart upptagna delen av bomb-C14-pulsen är försumbart liten ger själva observationen direkt belägg för att ytvattnet inte är av någon signifikant betydelse överhuvud taget för det egentliga havets upptag av atmosfäriska koldioxidöverskott (annat än som ett transportförmedlande gränsskikt). Ytvattnet svarar för en försumbart liten del av totalupptaget och har en försumbar inverkan på upptagsfarten. Därav följer att man vid beräkningar av hur snabbt antropogena koldioxidutsläpp tas upp i havet inte vinner något på att göra åtskillnad mellan ytvattnet och det egentliga havet.
Kontentan av vad som ovan sagts är att man inte kan lita ett skvatt på beräkningar gjorda med kolcykelmodeller som utgår från Ekv. (2) och tilldelar Revellefaktorn R ett fixt värde i närheten av 10. Inte ens värdet R=1 är acceptabelt, eftersom kolcykelsystemet kommer att befinna sig fjärran från jämvikt så länge vi släpper ut stora mängder fossil koldioxid och temperaturen inte behagar hålla sig någorlunda konstant på sekelnivå. För fixa värden på R representerar Ekv. (2) ingenting annat än en amatörmässig och matematiskt felaktig beskrivning av vad som karakteriserar lösningen till de kinetiska differentialekvationerna för koldioxid-utbytet mellan luft och hav.
Revelle-Suess ska ha en eloge för att de var bland de första som rapporterade ett experimentellt bestämt värde (τ =10 år) på koldioxidens relaxationstid, dvs. det som flertalet forskare tycks avse med begreppet ”uppehållstid”. De påpekade också att relaxationstiden, tolkad i ljuset av en luft/hav-modell, kan likställas med inverterade värdet (1/k1) av hastighetskonstanten för koldioxidens överföring från luften till havet (dvs. det som IPCC definierar som ”uppehållstid”). Det innebär att havsupptaget av antropogena koldioxidutsläpp sker med en fart som nära nog helt och hållet styrs av luftens koldioxidhalt enligt massverkans lag. Revelle-Suess tolkning av vad τ ≈ 1/k1 står för håller även efter en jämviktsapproximation, om man med ”havet” menar ”det egentliga havet”.
Följaktligen förmår vare sig beaktandet av ytvattnet som en separat del av havet, förutsättningen att koldioxidens luft/ytvatten-jämvikt inställer sig omedelbart, eller ytvattnets speciella karbonatkemi undanröja det som ett otal forskare har påpekat det senaste halvseklet: Koldioxidens relaxationstid/uppehållstid är enligt en uppsjö av experimentella observationer alldeles för kort för att antropogena utsläpp ska kunna vara det enda eller det helt dominerande skälet till att luftens koldioxidhalt har ökat under industriell tid (eller åtminstone efter 1958 enligt Keelingkurvan).
Andra faktorer måste ha bidragit till att koldioxidhalterna ökat. Termisk avgasning under 1900-talets globala uppvärmning har med säkerhet gjort det. Det var därför jag utvidgade Revelle-Suess luft/hav-modell till att på enklast tänkbara sätt beakta temperaturberoendet av koldioxidens vattenlöslighet. Det resulterade i den termiska luft/hav-modellen vilken, trots sin extrema enkelhet, tillfredställande beskriver såväl Keelingkurvan som kurvans temperaturberoende El Niño-fluktuationer och bomb-C14-kurvan. Allt detta för en uppehållstid (14 år) i samma storleksordning som samtliga hittills rapporterade experimentella skattningar av uppehållstiden och relaxationstiden.
De IPCC-stödda kolcykelmodellerna hänför de ökande koldioxidhalterna enkom till antropogena utsläpp, och förmår även de återge Keelingkurvan. Men det är en förmåga de bibringats genom införandet av en fiktiv konstant (Revellefaktorn) i ett teoretiskt felaktigt samband, vilket på konstlad väg drastiskt minskar såväl farten som omfånget av havets beräknade upptag av luftkoldioxid.
Gravt felaktiga modeller kommer obönhörligen på kant med verkligheten. Det är därför IPCC varit tvungna att negligera termisk avgasning, att hävda att C14-koldioxid bär sig annorlunda åt än antropogen koldioxid, samt att söka bortförklara varför alla experimentella skattningar av koldioxidens relaxationstid (τ), liksom alla skattningar av koldioxidens uppehållstid (1/k1), gett värden i storleksordningen 10 år. Ohållbarheten i IPCC:s kolcykelbedömningar har jag berört i tidigare inlägg. Här kan det räcka med att som avslutning visa figuren nedan, vilken belyser hur galet man hamnar när man i brist på adekvat kompetens fäster större vikt vid förutfattade meningar och hemmasnickrade osunda teorier än vid de observationer som gjorts.
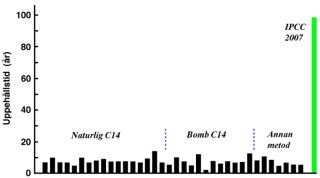
Figur 2. Svarta staplar visar experimentella skattningar av koldioxidens relaxationstid/
uppehållstid enligt sammanställningar refererade i Appendix till boken Falskt Alarm.
Grön stapel visar IPCC:s bedömning av koldioxidens apparenta uppehållstid (e-fold time), verbalt angiven som 50–200 år, men i figuren återgiven som 96 år vilket är det värde som
svarar mot IPCC:s specificering av Bernmodellens ”impulse response function”.
Professor emeritus i Fysikalisk Kemi vid KTH. Klimatdebattör sedan 2003.







Tack Gösta Petterson.
Två reflexioner utan att jag förstått allt.
Går det inte att fastställa i labmiljö?
Har den årsvariation man ser i luft CO2 på Hawai någon relevans?
Tack för en mycket bra redogörelse.
Tack Gösta! Du skriver pedagogiskt så att även en amatör begriper åtminstone delvis. Alltid när jag hör om något nytt försöker jag att göra mig en bild av mängder, man misstar sig annars ofta på det. Vad säger du om följande jämförelser (ppm avser det vikt eller volym)?
Om luft vore som vatten vore det 10 m djupt.
Av det utgörs 4 mm av koldioxid.
Av det tillförs antropogent 0,03 mm/år.
Havet är i genomsnitt 5 000 000 mm djupt.
Luften innehåller nära 800 Gton kol i form av koldioxid.
Antropogen tillförsel är ca 6 Gton/år.
Haven innehåller 40 000 Gton kol huvudsakligen i from av kalk (?) som motverkar havens ph-förändring.
Där har vi litet proportioner att utgå från.
Hur djupt ligger ’flaskhalsen’?
Hur avtar koldioxiden (ekvivalent) från luften och ned i djuphavet?
Som svar till Gösta citerar Peter Stilbs: ” det hela är inte så enkelt som vissa tror. Dra öronen åt Dig om någon yrar om Henry’s lag. Den är bara del av ett större skeende, där CO2 lokalt är i delvis jämvikt med bikarbonat HCO3- och karbonat CO3– – och uppslammad eller sedimenterad CaCO3.”
https://www.klimatupplysningen.se/2010/10/12/goteborg-snart-under-vatten/
Jag har rentav för mig att Peter Stilbs gjorde en grov beräkning av revellefaktorn i en kommentar här på bloggen (eller möjligen medan den hette TCS) för många år sedan innan Gösta dök upp med sina idéer. Kunskapsnivån här på bloggen verkar sjunka med åren.
Och du Thomas P gör ju fler inlägg än nån annan här, och dom bidrar verkligen till att kunskapsnivån sjunker.
Thomas P #4 – har Du inget bättre att komma med?
Mig veterligen har jag aldrig gjort något inlägg om Revellefaktorn.
Att jag den gången tog upp ”Henry’s lag” var närmast pga en annan skeptikers skeva uppfattning att havets jämvikt med CO2 i atmosfären följde samma lagar som koldioxidjämvikten i gränsytan luft/destillerat vatten.
(Se ex https://chemengineering.wikispaces.com/Henry's+Law )
Peter #6 Jag som tyckte det var rätt elegant att citera dig när du publicerat det där gästinlägget av Gösta Pettersson. Men jag kan väl dra upp lite mer:
1. Som redan konstaterats gäller Henrys lag för lösta gaser men ytterst liten del av CO2 förblir löst gas i havet utan det blir till karbonat och bikarbonatjoner.
2. Man får av GP intryck av att Revellefaktorn är något godtyckligt man hittat på när den i själva verket är en naturlig följd av balansen mellan CO2, HCO3- och CO3–.
3. Revellefaktorn gäller när man nått jämvikt i en vattenmassa, det är alltså den maximala mängd CO2 havet kan ta upp. För att få bättre beskrivning av en dynamisk situation där CO2 halten stiger får man ta till mer komplexa modeller som Bernmodellen som beskriver kolflöden i havet och på land.
4. Stycket som inleds ”Bolin-Erikssons grundförutsättning att luftens koldoxid alltid befinner sig i jämvikt…” är ett rent hjärnsläpp. GP skapar en dynamisk ekvation för förändring av halter och antar sedan att det inte förekommer några förändringar och får då inte oväntat 0=0. Detta tar han på något obegripligt sätt till intäkt för att man inte kan härleda någon revellefaktor när allt han gjort är att visa att det är olämpligt att använda en dynamisk ekvation i en statisk situation.
5. ”Det är därför IPCC varit tvungna att negligera termisk avgasning, att hävda att C14-koldioxid bär sig annorlunda åt än antropogen koldioxid, samt att söka bortförklara varför alla experimentella skattningar av koldioxidens relaxationstid (τ), liksom alla skattningar av koldioxidens uppehållstid (1/k1), gett värden i storleksordningen 10 år. ”
(Jag tror jag råkade skicka ut en halvfärdig kopia av inlägget tidigare)
Peter #6 Jag som tyckte det var rätt elegant att citera dig när du publicerat det där gästinlägget av Gösta Pettersson. Men jag kan väl dra upp lite mer kritik om du vill:
1. Som redan konstaterats gäller Henrys lag för lösta gaser men ytterst liten del av CO2 förblir löst gas i havet utan det blir till karbonat och bikarbonatjoner.
2. Man får av GP intryck av att Revellefaktorn är något godtyckligt man hittat på när den i själva verket är en naturlig följd av balansen mellan CO2, HCO3- och CO3–. Av någon anledning väljer dock GP att inte diskutera kemin.
3. Revellefaktorn gäller när man nått jämvikt i en vattenmassa, det är alltså den maximala mängd CO2 havet kan ta upp. För att få bättre beskrivning av en dynamisk situation där CO2 halten stiger får man ta till mer komplexa modeller som Bernmodellen som beskriver kolflöden i havet och på land. Hela GP:s kritik baserad på att man inte är jämvikt är alltså något som redan finns med i alla kolcykelmodeller.
4. Stycket som inleds ”Bolin-Erikssons grundförutsättning att luftens koldoxid alltid befinner sig i jämvikt…” är ett rent hjärnsläpp. GP skapar en dynamisk ekvation för förändring av halter och antar sedan att det inte förekommer några förändringar och får då inte oväntat 0=0. Detta tar han på något obegripligt sätt till intäkt för att man inte kan härleda någon revellefaktor när allt han gjort är att visa att det är olämpligt att använda en dynamisk ekvation i en statisk situation.
5. ”Det är därför IPCC varit tvungna att negligera termisk avgasning, att hävda att C14-koldioxid bär sig annorlunda åt än antropogen koldioxid, samt att söka bortförklara varför alla experimentella skattningar av koldioxidens relaxationstid (τ), liksom alla skattningar av koldioxidens uppehållstid (1/k1), gett värden i storleksordningen 10 år. ”
Allt det här är fel vilket ältats åtskilliga gånger i tidigare inlägg av GP. Detta är inte vad IPCC säger. Den kortare tid för CO2 GP drar upp handlar dessutom om livslängden för CO2-molekyler i atmosfärer vilket inte är detsamma som hur förändringen av CO2-koncentration ändras.
Härligt att se att du Thomas P höjer kunskapsnivån här på bloggen. Jag bugar och tackar för fantastiska inlägg. Äntligen skriver du nåt som man förstår.
Lasse #1
I labmiljö har man sedan länge konstaterat att destvatten försuras när det löser koldioxid.
Vad som händer om destvattnet även innehåller kalciumjoner har Tom Segalstad åskådliggjort i ett trevligt undervisningsexperiment på Youtube (https://www.youtube.com/watch?v=sjxUwDTkd4g); det fälls ut kalciumkarbonat vilket fixerar lösningens pH. Ytterligare tillsats av koldioxid ökar bara mängden utfällning. Tillsats av vätejoner minskar bara mängden utfällning. Så länge det finns kalciumjoner nog respektive utfällning kvar.
Vad som händer i havet lär förbli tämligen omöjligt att reproducera i labmiljö.
Årstidsfluktuationerna av luftCO2 på Hawaii återspeglar säkert bland annat effekter av temperatur och pH på gasens snabba jämviktning mellan luft och ytvatten, men påverkas även av ett otal andra faktorer vars relativa betydelse inte ens Keeling själv förmådde reda ut.
Tack Gösta. Det var en ren njutning att läsa detta inlägget.
# 10 GP
Är aningen skeptisk till TS: s experiment, han hävdar att syret blir koldioxid som sedan löser sig i vattnet och då får vattnet att stiga. Är det inte så att luften i glaset svalnar när ljuset släcks och det är huvudorsaken till att vattnet stiger?
Jag har i många år velat göra samma experiment (gammalt folkskolestoff, där man normalt använde vanligt vatten) , men med havsvatten istället för vad han nu hade. Han talar om Ca++-joner men det är oklart vad det egentligen var i vattnet.
Segalstad har ju havsvatten i Oslo, men jag har inget med rätt sammansättning här nära Stockholm
Tillägg: Hm … jag läste nu hela texten, och han har tydligen kalciumhydroxid i vattnet. Inte helt relevant, men visst hjäper det till att ”suga upp” koldioxiden från ljuset. Men det ska gå med vanligt vatten också.
Gösta och Peter, Experimentet med att spruta ut CO2 i havet har redan gjorts helt naturligt:
”Just about 100 yards from shore, and in waters 6 to 15 feet deep (2 and 3 meters), the volcanic vents create an underwater landscape that transitions from normal pH (8.1) to pH levels projected to arrive by the year 2100 (7.8), to highly acidic conditions (in the highs 6s and low 7s).”
http://www.livescience.com/16133-seafloor-volcanic-vents-ocean-acifidication.html
Nog kan man sänka pH.
Om man söker på Google på detta grundskoleexperiment : candle experiment with jar
så får man ganska många hits och även videos. Många hävdar att det är fel att tro att CO2 sugs upp i vanligt vatten, utan att det snarare är kontraktion av varm gas.
Men det är ju inte rätt – det var ju aldrig någon gasexpansion i kärlet innan
Nu fattas bara att havens densitet sänks på grund av CO2 upptaget för att också förklara havsnivåhöjningen.
Lars Cornell #3
Jag har inga större invändningar mot vad du säger, mer än att havets medeldjup av Wikipedia anges till omkring 3729 meter samt att kol huvudsakligen torde föreligga som vätekarbonatjoner i havet.
Var gränsen mellan ytvatten och det egentliga havet går har bl. a. diskuterats av Sundquist et al. i den artikel jag länkade till. Sundquist angav att djupet till gränsen med säkerhet är mindre än 100 meter.
Och som alltid vid modellering av komplexa förlopp är ett basalt problem att modeller måste utgå från en förenklad bild av förloppen. Gränsen mellan ytvattnet och det egentliga havet är förmodligen suddig.
Likaså föreligger det troligen en gradient i kolets fördelning från havsytan till djuphaven och lokala variationer av denna gradient (jag är tyvärr inte tillräckligt insatt i detta för att kunna ge dig någon vettig referens), medan man med boxmodeller tilldelar havets kolinnehåll ett tänkt globalt genomsnittligt värde. Precis som man tilldelar temperaturen ett tänkt globalt genomsnittligt värde och luftens koldioxidhalt ett tänkt globalt genomsnittligt värde (ppm avser normalt volym).
Huruvida en modell trots sådana förenklingar kan betraktas som vettig eller ej avgörs av i vilken mån den förmår beskriva de observationer som gjorts.
Gösta #17 ”Likaså föreligger det troligen en gradient i kolets fördelning från havsytan till djuphaven”
Visst, djuphaven innehåller mer kol pga den biologiska pump där organismer vid ytan tar upp CO2 och (delvis) sjunker mot havsbotten när de dör och där bryts ned till CO2 igen.
Lite OT – vår kära förutsägbara Granskningnämnd för Radio och TV friar givetvis även icke politiskt korrekta inslag, bara de har tillräckligt vänsterstuk – vem hade väntat sig annat?
http://www.svd.se/kultur/granskningsnamnden-friar-farrokhzad_4302999.svd
Thomas P #4
Vad jag förstår vänder Peter och jag oss mot exakt samma sak: Åberopandet av Henrys lag i sammanhang där den inte är giltig.
För att citera mitt inlägg: (Jämviktssambandet Henrys lag) ” kan INTE användas för att fastställa relationen mellan luftens halt av koldioxid och halten karbonatföreningar i det egentliga havet, eftersom koldioxidutbytet mellan luft och det egentliga havet befinner sig fjärran från jämvikt.”
#17 Gösta, tack för ditt svar.
När man inte är yrkesverksam kemist måste man tänka på litet annorlunda sätt för att kunna förstå. Mitt sätt att tänka är då vad som händer när en syra (koldioxid + vatten) möter det basiska material i form av kalk som finns i riklig mängd både i löst och fast form i havet och dess omedelbara närhet. Jag tänker då på koraller, kalksand och kalkklippor. Mängden sådant basiskt material måste rimligen vara överväldigande mycket större än den antropogena koldioxid som hamnar i havet. Mängden antropogen koldioxid kommer inte under närmaste miljoner år att kunna ’övermanna’ havens basiska förråd. Eller hur?
Slutsatsen blir, att om luftens koldioxidhalt ökar till säg 800 ppm, vilket kan vara önskvärt, kommer ph-värdet i ytvattnet att förskjuts litet men inte mycket för att snabbt stabiliseras på en ny helt riskfri nivå.
Något som jag saknar i diskussionen är havets fotosyntes. Hur mycket koldioxid tar den hand om och vilken blir restprodukten?
#18 ThP. Ja, och den koldioxiden kommer med tiden upp till ytan och överförs till atmosfären. Om inte skulle haven surpla i sig allt koldioxid och allt på land levande dö.
Gösta #20 ”Vad jag förstår vänder Peter och jag oss mot exakt samma sak: Åberopandet av Henrys lag i sammanhang där den inte är giltig”
Det är ett vällovligt syfte speciellt som det mest är ”skeptiker” som ägnar sig åt detta, men tyvärr hör du till de som åberopar denna lag i samband den inte är giltig, typ när du skriver ”Inom denna box styrs enligt jämviktsapproximationen kolets fördelning mellan luft och ytvatten av Henrys lag.” Du försöker här trolla bort revellefaktorn som gör att havet kan ta upp mycket mindre CO2 än man naivt kan tro om man tillämpar Henrys lag.
Thomas P säger att Gösta försöker ”trolla”, i den grenen är du Thomas P i särklass.
Hej Gösta,
Grattis till detta mycket intressanta resonemang som skissar upp en mycket slående vetenskaplig förklaring till att din enkla kolcykelmodell (GP-modellen kallar jag den) så väl beskriver observationerna, dvs. Keelingkurvan, Keelingkurvans derivata, speciellt de El-Niñorelaterade variationerna, samt bombkurvan.
Detta slår ju övriga kolcykelmodeller som FNs klimatpanel (IPCC) redogör för i sin senaste vetenskapliga rapport med hästlängder vad jag kan förstå (men det finns mycket dimma i klimatpanelens framställning av dessa saker). Det har varit ett sådant här resonemang som du nu redogör för i ditt blogginlägg som har fattats för att GP-modellen skall komma till sin fulla rätt. Nu finns ett sådant djupgående vetenskapligt resonemang som förklarar varför GP-modellen stämmer så bra med observationerna.
Vi får nog konstatera att förmodligen endast vi som har en bakgrund som kemivetenskapliga professorer fullt ut kan uppskatta ditt resonemang, men om man inte har den bakgrunden så är nog risken stor att man saknar tillräckliga kunskaper i ämnet. Jag ser att Thomas ändå försöker sig på att opponera men han har tydligen inte förstått så mycket av ditt resonemang.
Jag har också funderat på Bolin-Erikssons resonemang om att det omblandade ytskiktet skulle bli en flaskhals på grund av jämviktsantagandet. Koldioxidens kemiska potential blir då praktiskt taget lika i atmosfär och det omblandade yskiktet. Massöverföringshastigheten av koldioxid från gasfasen till ytskiktet bestäms av en mindre än en millimeter tunn laminär film med en mycket liten gradient i kemisk potential för koldioxid som drivande kraft.
Om man nu gör tankeexperimentet att det under det omblandade ytskiktet finns ett tunt atmosfärskikt innan resten av havet tar vid. Då skulle koldioxiden överföras till detta atmosfärskikt efter passage av en likadan tunn laminär film i det omblandade ytskiktet. Därefter skulle koldioxiden absorberas i resten av havet genom en motsvarande tunn laminär film. Det finns ingen som helst antydan till att det omblandade ytskiktet skulle bli en flaskhals enligt detta resonemang.
Det finns heller ingen logik, som jag kan se, att det skulle uppstå någon väldig effekt av att detta atmosfärsskikt skulle försvinna och det omblandade skiktet och resten av havet återigen vore i direktkontakt. Alltså, om vi för in den kemiska potentialen som en drivande kraft så får jag inte ihop det med att det omblandade skiktet skulle vara en flaskhals. Bolin och Eriksson resonerar bara i termer av koncentration av koldioxidmolekyler, inte i termer av kemisk potential som drivande kraft.
Men detta är naturligtvis bara ett spontant resonemang från mig i en bloggdiskussion, det kan finnas något jag förbisett.
# 15 Peter S
Gasen är nog rätt varm från början och experimentet fungerar ju med kranvatten?
Thomas #8
1. Som redan konstaterats gäller Henrys lag för lösta gaser men ytterst liten del av CO2 förblir löst gas i havet utan det blir till karbonat och bikarbonatjoner.
Som Gösta mycket tydligt har påpekat så gäller proportionaliteten, dvs. Henry’s lag, även om koldioxiden löses i en lösning med karbonat- och bikarbonatjoner om pH hålls konstant.
2. Man får av GP intryck av att Revellefaktorn är något godtyckligt man hittat på när den i själva verket är en naturlig följd av balansen mellan CO2, HCO3- och CO3–. Av någon anledning väljer dock GP att inte diskutera kemin.
Teorin för revellefaktorn som den använts i utvecklingen av kolcykelmodellerna har utgått från antagandet att det omblandade skiktet inte utbyter vätejoner eller hydroxidjoner med resten av havet. Inte heller har man tagit hänsyn till levande organismers förmåga att konsumera eller producera sådana joner. Därför kan man mycket väl säga att revellefaktorn är något godtyckligt.
3. Revellefaktorn gäller när man nått jämvikt i en vattenmassa, det är alltså den maximala mängd CO2 havet kan ta upp. För att få bättre beskrivning av en dynamisk situation där CO2 halten stiger får man ta till mer komplexa modeller som Bernmodellen som beskriver kolflöden i havet och på land. Hela GP:s kritik baserad på att man inte är jämvikt är alltså något som redan finns med i alla kolcykelmodeller.
Teorin för revellefaktorn för hela havet bygger på antagandet att vattenmassan uppnår ett metastabilt jämviktstillstånd som hålls kvar i det metastabila läget av att de processer som leder till den slutliga kemiska jämvikten är väldigt långsamma. Det vetenskapliga stödet för att en sådan teori faktiskt skulle kunna gälla med påstådda tidsskalor är enligt min mening mycket bräckligt. Speciellt att GP-modellen stämmer så bra med observationer och att man kan förklara varför är enligt min mening mycket problematiskt för denna teori.
4. Stycket som inleds ”Bolin-Erikssons grundförutsättning att luftens koldoxid alltid befinner sig i jämvikt…” är ett rent hjärnsläpp. GP skapar en dynamisk ekvation för förändring av halter och antar sedan att det inte förekommer några förändringar och får då inte oväntat 0=0. Detta tar han på något obegripligt sätt till intäkt för att man inte kan härleda någon revellefaktor när allt han gjort är att visa att det är olämpligt att använda en dynamisk ekvation i en statisk situation.
Här är Thomas invändning faktiskt obegriplig för mig medan Göstas resonemang för mig framstår som en skarpsynt observation.
5. ”Det är därför IPCC varit tvungna att negligera termisk avgasning, att hävda att C14-koldioxid bär sig annorlunda åt än antropogen koldioxid, samt att söka bortförklara varför alla experimentella skattningar av koldioxidens relaxationstid (τ), liksom alla skattningar av koldioxidens uppehållstid (1/k1), gett värden i storleksordningen 10 år. ”
Allt det här är fel vilket ältats åtskilliga gånger i tidigare inlägg av GP. Detta är inte vad IPCC säger. Den kortare tid för CO2 GP drar upp handlar dessutom om livslängden för CO2-molekyler i atmosfärer vilket inte är detsamma som hur förändringen av CO2-koncentration ändras.
Gösta har helt rätt i att FNs klimatpanel negligerar termisk avgasning på det sätt som denna ingår i GP-modellen. Därför är det heller inte konstigt att man inte i klimatpanelens rapport kan finna några resultat sådana som GP-modellen har producerat (se ovan). Detta kan enkelt förklaras av att de kolcykelmodeller som FNs klimatpanel tar upp i rapporterna helt enkelt inte klarar av att ge dessa resultat.
Om man baserar resonemang om koldioxidens medeluppehållstid och dess relaxationstid på de idéer som ligger till grund för klimatpanelens kolcykelmodeller blir det naturligtvis fel om dessa modeller bygger på felaktiga grunder. Eftersom GP-modellen bygger på i väsentliga avseenden andra grunder så ger den en annan bild av dessa tider.
Om ni är så övertygade om att ni ”som har en bakgrund som kemivetenskapliga professorer” har så mycket på fötterna föreslår jag som tidigare att ni ger er ut på det verkliga slagfältet och publicerar detta i vetenskaplig tidskrift där det kan bedömas av personer som är experter på kolcykelkemi inte bara av amatörer på en blogg för troende. Själv tycker jag Gösta och Pehr mest kommer med snömos, men vad vet jag som inte har någon bakgrund som kemivetenskaplig professor…
Där ställde du en bra fråga Thomas P, som tål att funderas på, ”men vad vet jag”.
Thomas #27,
Jag själv kan naturligtvis inte publicera Göstas resultat. Detta vore ju plagiat, eller hur.
Gösta har ju deklarerat att han inte vill publicera sina resultat på annat sätt än genom en webbsida. Jag kan förstå honom med tanke på den politisering av vetenskapen på detta område som har skett vilket är knepigt för en pensionerad forskare att hantera.
Min åsikt är att kolcykelforskare inte kan negligera sådana resultat av en kompetent forskare inom kinetikområdet som Gösta har publicerat om de vill framstå som seriösa. Även om dessa resultat inte är publicerade på vanligt sätt så finns de där och frågan om hur man från kolcykelforskarhåll vill förklara saken har väckts och pockar på svar. Med tanke på att saken har diskuterats på många olika klimatbloggar, om än amatörmässigt, så kan man från kolcykelforskarhåll inte bara säga att man är omedveten om detta.
Att man har ignorerat detta från kolcykelforskarhåll hittills kan dock ha en förklaring i att det resonemang som Gösta presenterar i blogginlägget här, som förklarar varför GP-modellen stämmer så bra med observationer, inte har funnits med tidigare. Så vi får väl avvakta ett tag till innan vi börjar ställa krav på att man från kolcykelforskarhåll kommer med en förklaring.
Min gissning är att denna vetenskapliga fråga har genomdiskuterats och värkt ut om fem till tio år och att det är mer sannolikt än osannolikt att Gösta då allmänt erkänts att ha fått rätt, helt eller delvis.
Thomas påstår för övrigt i #27 att detta är ”en blogg för troende” och att det jag skriver är ”snömos”. Detta är ju rena propagandauttryck, och att komma med sådant i en vetenskaplig diskussion, som vi för i denna tråd, är oseriöst.
Kan inte bedöma detaljerna i denna drabbning men misstänker att de ”kemivetenskapliga professorerna” sopade banan med den djupt troende Thomas P haha. …:-)
# 15 Peter S
Bästa förklaringen jag sett: förbränningen CH4 + 2×02 -> 2xH20 + C02 ersätter två syremolekyler men en C02 + vatten som kondenseras på glaset. Mängden gas minskar men detta kompenseras av uppvärmningen. När ljuset slocknar så svalnar gasen och vattnet stiger. Att C02 löser sig i vattnet är inte orsaken till det snabba förlopp som man ser.
Thomas P #8
1. Bolin-Eriksson förklarade varför Henrys lag vid jämvikt även kan användas för att relatera lufthalten av CO2 till havshalten av karbonatföreningar i allmänhet.
2. Jag utgår från att Bolin-Eriksson korrekt har analyserat jämviktskemin för vattnets karbonatföreningar under de av dem preciserade förutsättningarna (försumbar fastfas av karbonater, inga andra system som påverkar pH). Vad jag vänder mig mot är att de använder jämviktssambanden för att karakterisera storheten R i Ekv. (2) som hänför sig till variabler som INTE är i jämvikt med varann.
3. Samma invändning måste resas mot alla kolcykelmodeller som försöker beskriva systemets dynamik med hjälp av parametrar (Revellefaktorn) och samband som härletts med jämviktsberäkningar.
4. Det är inte jag, utan Bolin-Eriksson som skapat en dynamisk ekvation för halter samtidigt som man förutsatt att det inte förekommer några förändringar; min roll inskränker sig till att referera vad dom säger och att invända mot deras slutsats. Jag är glad att du inser det orimliga i deras resonemang, men tycker du är orättfärdig när du karakteriserar deras misstag som ”ett rent hjärnsläpp”. Deras analytiska tillvägagångssätt tyder snarare på bristande reaktionskinetisk kompetens och därav följande oförmåga att korrekt behandla den i övrigt godtagbara tanken att luftkoldioxiden jämviktar snabbt med ytvattnet.
5. Eftersom jag redan ”ältat” mina invändningar mot IPCC:s bedömningar i tidigare inlägg avstår jag från att upprepa mig i det avseendet. I stället ska jag inrikta mig på ditt påstående
”Den kortare tid för CO2 GP drar upp handlar dessutom om livslängden för CO2-molekyler i atmosfären vilket inte är detsamma som hur förändringen av CO2-koncentration ändras”
vars sanningshalt jag inte kan uttala mig om eftersom jag inte vet hur du definierar dina begrepp ”livlängden av en molekyl” och ”förändringen av koncentrationsändringen”.
Men jag vet att experimentella data i Fig. 2 till övervägande delen representerar bestämningar av koldioxidens relaxationstid (tau) definierad som tidskonstanten för ett monoexponentiellt bortskaffande av koldioxidöverskott ur luften, dvs. precis den parameter som avgör hur länge antropogena koldioxidutsläpp håller sig kvar i luften. I enstaka fall har man även bestämt uppehållstiden så som den definieras av IPCC (dvs 1/k1), varvid man kunnat bekräfta att tau ≈ 1/k1. Bestämningarna har vidare genomförts med minst 6 olika metoder och i samtliga fall gett värden i storleksordningen 10 år.
IPCC har försökt bortförklara dessa resultat med att luftöverskott av koldioxid ”i själva verket” (dvs. enligt Bernmodellen och liknande kolcykelmodeller) bortskaffas i ett flerfasiskt förlopp varav experimentalister endast bestämt relaxationstiden för det snabbaste förloppet. Någon sådan flerfasiskhet har aldrig observerats. Tvärtom visar bomb-C14-kurvan att avklingningen sker monofasiskt, varför IPCC även tvingats söka bortförklara denna observation med att C14-koldioxid inte bär sig åt som antropogen koldioxid.
Allt för att kunna hålla fast vid den förutfattade meningen att ökningen av luftens koldioxidhalt helt och hållet orsakats av antropogena koldioxidhutsläpp. De experimentella observationerna ger inget stöd åt ett sådant överförenklat synsätt, ej heller korrekt härledda modeller. Det är nog ingen slump att IPCC:s skattning av den apparenta uppehållstiden i Fig. 2 överstiger de experimentella värdena med en faktor som överensstämmer väl med den i de IPCC-stödda modellerna osunt införda Revellefaktorn.
Lars Cornell #21
Enligt växtfysiologer svarar havsorganismer för ungefär hälften av biosfärens totala fixering av koldioxid. För alla växter gäller att ungefär hälften av den fixerade koldioxiden blir till mat som växterna själva äter upp (förbränner till koldioxid i fotorespirationen) inom loppet av ett dygn. Resten hamnar väl till helt övervägande del i näringskedjan. På något sätt.
Thomas P #22
”tyvärr hör du till de som åberopar denna lag i samband den inte är giltig”
Du har fel. Jämviktsapproximationen medför att Henrys lag kan tillämpas inom luft/ytvatten-boxen.
Och så tycks du inte förstå att jag i det av dig nämnda sammanhanget försvarar Bolin-Erikssons tänkande och deras förmodande att det kan föreligga en ”Revelle-effekt” i bemärkelsen en försurning av ytvattnet som leder en minskning av dess förmåga att ta upp koldioxid.
Du vänder dig i själva verket mot Bolin-Erikssons resonemang (de använder sig av Henrys lag vid härledningen av sina samband). Jag försvarar deras resonemang, men med reservationen att det endast är giltigt för ytvattnet och inte kan extrapoleras till att gälla det egentliga havet vid en matematiskt korrekt införd jämviktsapproximation.
Johan M #32 Peter Stilbs #15
Anledningen till att jag nämnde Segalstads undervisningsexperiment var att jag ville dra uppmärksamhet till karbonatutfällningen, vilken fixerar systemets pH vid jämvikt (jämför Lars Cornells kommentar #21). Men filmsnutten gav oss uppenbarligen även anledning att tänka vidare på vad man ser.
Metan är inte en speciellt god modell för förbränningen av stearinsyra eller paraffin [det senare utgör en blandning av högmolekylära alkaner och kan lämpligen approximeras som (-CH2-)].
Stearinsyra: C17H35COOH + 27O2 ——- !8CO2 + 18H2O
Paraffin: (-CH2-)2n + 3nO2 ——– 2nCO2 + 2nH2O
I båda fallen (dvs oavsett ljusets kvalitet) ersätts vid förbränningen 3O2 med 2CO2.
Fall A: Om all CO2 tas upp i vattnet borde luftvolymen (vid fix temp) minska med 18%.
Fall B: Om ingen CO2 tas upp i vattnet borde luftvolymen minska med en tredjedel av 18%, dvs 6%.
Då omformar jag raskt Segalstads glas till en cylinder med lite fingerspitzgefühl och finner med linjal att cylinderns topp på min skärm ligger 60 mm ovan vattenytan. Vattenstigningen inne i glaset svarar mot 10 mm, dvs mot en luftvolymminskning på 1/6 ≈ 17%. Oförenligt med Fall B, speciellt om man misstänker att luften har värmts upp något av ljuset, men helt förenligt med Fall A.
Därför tror jag Segalstad har helt rätt. Experimentet belyser även hur snabbt koldioxid löser sig i vattnet, styrkt av det fälls ut kalciumkarbonat i vattenfasen. Jämvikten ställer in sig på några sekunder, precis som jag tyckte mig minnas från den tid på 1960-talet när jag som doktorand studerade processen ifråga.
Tack för svar GP.
Den process du beskriver är en av fundamenta i vattenrening.
Lufta bort CO2 så blir vattnat mindre aggresivt mot järnrören. Vill man uppnå lägre aggresivitet kunde man låta vattnet strömma genom Ca CO3 innan luftningen för att få bäst utlösning vill jag minnas.
pH justering har också använts för att fälla ut föroreningar främst Fe och Mn.
Pehr #29 ”Jag själv kan naturligtvis inte publicera Göstas resultat. Detta vore ju plagiat, eller hur.”
Nej, men du skulle kunna uppmuntra honom att publicera, rentav hjälpa till med det praktiska om du ville. Du vet ju hur man gör.
”Min åsikt är att kolcykelforskare inte kan negligera sådana resultat av en kompetent forskare inom kinetikområdet som Gösta har publicerat om de vill framstå som seriösa.”
Min åsikt är att jag inte sett något tecken på att en enda kolcykelforskare läser denna blogg eller Göstas hemsida och inte heller har de någon anledning att göra det. Gösta har inte publicerat någonting. Vad ni än tror är det vetenskaplig press, konferenser och liknande som gäller, men ni i er lilla ankdamm får väl tro att ni vet bäst och att forskarvärlden ignorerar er bara för att de inte har något svar, eller rentav att Gösta kommer visa sig få rätt i någon okänd framtid när resten av forskarna äntligen inser hans storhet.
#35
Är på resande fot men skall när jag kommer hem fylla en Soda Stream-flaska med kolsyra och vända den upp och ner i en skål med vatten. Då får man bort all effekt från värmen.
Kan inte du Thomas P göra som du anser att alla kolforskare och forskarvärlden gör, så slipper vi läsa dina meningslösa inlägg.
Thomas # 38…….”resten av forskarna” du menar förstås de 97 procenten som demokratiskt kommit överens om att de är 95 % säkra på ditten o datten som storm vindstilla kallt varmt regn snö torka översvämning våld flyktingar sjukdomar längs nya klimatzoner artutrotning bränder mm mm man matats med fy fan tänk att man själv trodde på dyngan för ca 10 år sen….jösses !
Ljuset i glaset –
provade lite hemma i köket för att försöka se hur stora effekter värme/koldioxid/volymminskning hade. Resultaten kanske är mer som en guide till vad man kan visa barnen men lite roligt är det.
1/ Klassikern – tänt ljus, vänd glaset upp och ner. Lågan brinner och efter bara ett litet tag kan man se att vattenytan rör sig, när lågan flämtar och dör stiger sedan vattnet till ca 1 cm.
2/ Värmepistol – med en värmepistol värmer vi upp luften i ett glas och vänder sen upp och ner på det. Resultatet blir att vattnet sakta men säkert stiger upp till ca 1 cm. Den svalnande luften har en effekt men inte så värst snabb.
3/ Varianten – håll glaset ovanför ljuset i drygt en minut så att det fylls med varm luft med hög koncentration koldioxid, sätt ner glaset över ljuset. Lågan slockna nästan omedelbart och vattnet stiger snabbt till 0.5 cm för att sedan sakta stiga till 1 cm.
4/ Sodastream – fyll en tom Sodastreamflaska men kolsyra, vänd upp och ner i en skål med vatten. Vattnet bubblar runt flaskmynningen men någon förändring av vatten nivån i flaskan märks inte?
Den avsvalnande luften har en effekt men kanske inte stå stor i det klassiska experimentet där glaset snabbt vänds upp och ner över ljuset. I varianten ser man tydligt att någonting sker mycket snabbt – det kan inte vara på grund av svalnande gaser och inte heller på grund av att volymen minskar. De första 0.5 cm kan förklaras med att koldioxiden löser sig i vattnet och resterande 0.5 cm på grund av den avsvalnande gasen.
Om 0.5 cm kan härledas till att koldioxiden tas upp i vattnet så skulle de återstående 0.5 cm i klassikern beror på den minskande volymen plus till mindre del av den avsvalnade luften.
Allt vore frid och fröjd om nu bara vattnet vill stiga i Sodastreamflaskan. Vad är det som händer? Att dte bubblar runt flaskan kan väl bero på att koldioxiden löser sig i vattnet men när detta vatten sen kommer ut runt mynningen så avges det snabbt som bubblor. Men varför ser vi ingen vattenstigning?
Johan M #43
Kemiprofessorerna har säkert det rätta svaret, men jag undrar om inte temperaturen har stor inverkan på slikt…?
Prova och värm upp sodastream flaskan efter laddning. Eller vattenbadet.
#43 JMH
>Prova och värm upp sodastream flaskan efter laddning. Eller vattenbadet.
jag provade med flaskan (varmare vatten håller mindre gas) och visst steg vattnet, men…. jag tog också en flaska med vanlig luft och värmde den under rinnande hett vatten och även där stiger vattnet så det är en effekt av avsvalnande luft.
Varför sörplas koldioxid från en brinnande låga upp av vattnet medans Sodastream-gas inte visar samma benägenhet? Måste vi ta till flogistoner för att reda ut det här 🙂
Johan M #44
Jag blev också sugen på att experimentera…
Provade med både iskallt vatten och (nästan) kokande vatten. Tänkte jag skulle se skillnad eftersom det varma vattnet kyler sämre än det kalla vattnet. Men, jag fick samma resultat. Dvs jag kunde inte se någon direkt skillnad med bara mitt ögonmått. En brinnande låga är ju förstås många hundra grader varmare (tippar på 500 – 1000, kanske närmre 500 pga syrebrist), och borde värma luften i glaset rejält, så om kylmedlet (vattnet) är noll eller hundra grader spelar kanske inte så stor roll.
Jag tror ju inte att det har med CO2 upptag att göra, så jag provade med matolja isf vatten. Jag har förstås ingen aning om även matolja kan ’suga’ upp CO2 som vatten, men jag tror iaf inte det…..
Hursomhelst blev det samma resultat, dvs vätskenivån (oljan i detta fall) steg precis lucka mycket som innan med vatten. Vad skulle det visa?
Hej Johan och JMH,
jag antar att det handlar om experimentet med ett ljus stående i ett vatten som man sänker ned ett glas över. När jag räknar på det så antar jag att stearin ”ser ut som” CH2 och i så fall är reaktionen att
2 CH2 + 3 O2 –> 2 CO2 + 2 H20
d.v.s. av tre molekyler syre får vi 2 molekyler koldioxid och 2 molekyler vattenånga. Vattenångan fångas naturligtvis in omedelbart av vattenbadet, men om inte koldoxiden infångades alls så skulle gasmängden i glaset minska med en tredjedel av en femtedel, d.v.s. med en femtondel. Det brukar dock ”se ut som” snarare en femtedel än en femtondel, vilket skulle innebära att nästan all koldioxid infångats.
Det borde gå att se skillnaden.
Jag tror att koldioxid löser sig ungefär lika bra i olja som i vatten. Eftersom koldioxidmolekylen är rak så är den inte polär vilket kan innebära att den löser sig i ett opolärt lösningsmedel som matolja. Jag tror till och med att förutsättningen för att den ska lösa sig så bra i vatten är att det mesta blir som bikarbonatjoner.
Sten Kaijser #46
Jo, det är just det experimentet. Jag googlade lite på stearin, och det är väl lite mer invecklat än CH2, men i princip tror jag du har rätt, det bildas CO2 och H2O vid förbränningen.
Jag körde mitt eget experiment ett varv till då jag insåg att jag tänkt fel. Vattnets yta är ju ganska liten och har inte så stor inverkan på kylningen som glasets yta, som är många gånger större. Jag provade alltså med ett varmt (kokande vatten) och ett kallt (frysen 30 min) glas, båda noga torkade (torra). I det kalla glaset steg ytan betydligt mer, samt det bildades mycket imma på glasets insida, detta observerades inte på det varma glaset. Man kan också se att vattenytan stiger mycket sakta under tiden lågan brinner, men när den slocknar gör vattenytan ett ’språng’.
Så här tror jag: När stearinet brinner bildas som sagt CO2 och H2O. H20 kondenserar på glasets insida, vilket kyler ’luften’ samt/och minskar dess volym. Att man inte ser någon expansion när lågan brinner beror på att avkylningen/kondensationen startar med en gång och balanserar expansionen. Att vattenytan gör ett ’språng’ när lågan slocknar beror på att lågan upptog en volym som ju försvinner när lågan försvinner.
Själv tror jag alltså inte att vattenytan och dess eventuella egenskaper har så stor inverkan. Vilket jag observerade i mitt förra experiment med olika temperatur på vattnet (ingen direkt skillnad).
Om man kunde fixa till en låga som brinner utan att det bildas CO2, eller någon annan gas som löses i vatten, men ändå med bildande av H2O skulle man få en referens. Förslag?
Jag kan efter lunch på stan och biobesök (Trevligt folk – rolig och mycket sevärd) konstatera att den Sodastremflaska som stått upp och ner i en skål med vatten hade en markant vattenstigning, nästan 1/3 av flaskan. Vilket skulle konfirmera att koldioxiden löser sig i vattnet. Förloppet verkar dock inte vara så snabbt som försöket med värmeljuset föranleder en att tro. Hmmm?
Hej JMH,
när det bildas imma på glaset så avges värme, dels till glaset, dels till luften. Förmodligen är det så att när det brinner så värms luften och håller emot det yttre trycket, d.v.s det som vill lyfta vattenytan, men luften kyls snabbt såväl av vattnet under som av glaset. Om glaset är varmt så bör det ta något längre tid innan vattnet stiger – inte för att koldoxiden upptas långsammare utan för att luften håller sig varm längre och kan motverka omgivningens tryck.
Efter en fotbollsträning kan jag meddela resultat från ytterligare experiment.
4/ Vattenånga – fyll ett glas med varm vattenånga genom att hålla det över kokande vatten, vänd upp och ner på tallrik med vatten. Vattenytan stiger rätt så snabbt upp till ca 1 cm, påminner en del om det klassiska experimentet.
Hade jag varit på landet hade hämtat upp lite släckt kalk men nu blir det melodifestival 🙂
Johan M #50
Och om man byter ut vattnet mot en syra, tex citronsyra, vad kan man vänta sig för resultat?
Sten Kaijse #49
Är det inte så att när vattenångan kondenserar sker en kraftig volymminskning?