Gösta Pettersson har i flera inlägg (Den gravito-termala effekten, Grand Canyon och växthuseffekten, Växthuseffekten enligt William Happer) pekat på att den s.k. gravito-termala effekten är huvudorsak till den temperaturgradient vi ser i troposfären och att den effekt som tillskrivs växthusgaserna därmed är överdriven. När jag läste Göstas första inlägg så var jag övertygad om att det stämde och såg det som ännu ett argument för att koldioxidhotet var överdrivet. Av en händelse höll jag på att leka med lite programmeringsövningar varav en var en simulator för partiklar. Det ena gav det andra och vad var inte enklare än att sätta upp en simulering som påvisade effekten – förbryllad kliade jag mitt huvud, ingen effekt visade sig. Innan jag förklarar simuleringen och de resultat den visar så kan vi i korthet gå igenom vad temperaturgradienten är och vad den gravito-termala effekten har med saken att göra.
Temperaturgradienten
Temperaturgradienten är det faktum att temperaturen sjunker med höjden i det som vi kallar troposfären (upp till ca 10.000 m.ö.h). Den varierar naturligtvis med var på jorden man är, om det är natt eller dag, fuktighet mm men vi kan i runda slängar säga att den är 6-10 grader per km. Att det blir kallare ju högre upp man kommer råder inget tvivel om men frågan är vad det beror på. En teori är att temperaturskillnaden beror på växthusgaser, att luften värms upp på lägre höjd av strålning från jordytan och kyls av på högre höjder där strålningen kan gå rakt ut i rymden. Vet vi hur denna temperaturgradient ser ut kan vi naturligtvis räkna på hur den skulle se ut om vi fördubblade mängden växthusgaser.
Den andra teorin är den s.k. gravito-termala effekten; den säger att temperaturskillnaden är en naturlig följd av gravitationen. Den gravito-termala effekten är viktig eftersom om hela eller delar av gradienten beror på gravitationen så ger det mindre utrymmer för växthusgaserna att spela en roll – en fördubbling av dessa skulle ha en mindre betydelse. Hur lyder då resonemanget om den gravito-termala effekten, och varför är det så svårt att bevisa om den finns eller inte?
Den gravito-termala effekten
Den gravito-termala effekten är faktiskt väldigt enkel att förklara, och kanske därför också väldigt svårt att förstå varför den inte finns. Temperatur är som alla vet relaterad till rörelse och det är den genomsnittliga rörelseenergin hos alla partiklar vi vill fånga. Rörelseenergi hos en enskild partikel är dess massa gånger dess hastighet i kvadrat delat med två; för vårt resonemang kan vi dock nöja oss med att komma ihåg att hastigheten på partiklarna bestämmer temperaturen. Betraktar vi en partikel i en gas så kan vi enkelt säga att den har en hastighet i en bestämd riktning och behåller den hastigheten och riktningen tills den krockar med en annan partikel. Detta är dock inte helt sant om den vi inte befinner oss på en rymdstation i omloppsbana runt jorden. Gravitationen påverkar naturligtvis även en liten partikel och dess rörelse är som vilken tennisboll som helst en kastparabel. En partikel som har riktning uppåt kommer att sakta ner en aning och en partikel som går neråt kommer öka sin hastighet. För den enskilde partikeln har detta minimal påverkan men för atmosfären har det naturligtvis stor påverkan – partiklar som befinner sig närmare jordytan har ökat i hastighet och de som befinner sig högre upp har minskat i hastighet. Som ett brev på posten får vi en temperaturgradient som när man räknar på det överensstämmer rätt väl med den gradient vi faktiskt har – vilket ger att bidraget från växthusgaser är högst begränsat.
Finns den gravito-termala effekten?
Söker man lite på nätet så hittar man artiklar som antingen fullt stödjer teorin om den gravito-termala effekten men man hittar även artiklar som helt avskriver den. Det verkar inte vara helt enkelt att övertyga någon med att analytiskt argument så varför inte prova en simulering för att se vad som händer. En simulering är iofs alltid en förenkling av verkligheten och det är lätt att man gör antaganden och begränsningar som har en avgörande betydelse men som man sedan inte ”kommer ihåg att man gjorde”. Globala klimatmodeller där man har gjort hur mycket antaganden och förenklingar som helst är väl ett exempel där man kan gå vilse och faktiskt tro att simuleringen är verkligheten. När man jämför med andra simuleringar (som gjort samma antaganden) som visar samma sak, så är slutsatsen klar som korvspad.
I just det här fallet tror jag dock att man kan göra en simulering eftersom det fenomen vi talar om är så enkelt – vi kan göra en mycket enkel modell och skall där kunna se effekten. Ser vi effekten i den enkla modellen så finns den (med det inte sagt att den i verkligheten spelar någon roll) men om vi inte ser den – så finns den inte. Den gravito-termala effekten är inte beroende av några konstiga parametrar som vi måste gissa, atmosfärens sammansättning eller jordens krökning – den finns i en tvådimensionell värld med identiska partiklar och fullständigt elastiska stötar….. och detta är väldigt enkelt att simulera.
En väldigt enkel värld
Det vi skall simulera är en väldigt enkel värld. För det första så kommer vi att röra oss i en tvådimensionell värld men en bredd och höjd men inget djup. Antaget är att om den gravito-termala effekten finns i en tredimensionell värld så finns den i en tvådimensionell värld. I en tvådimensionell värld så är alla partiklar cirklar och vi kommer bara göra simuleringar där alla partiklar är identiska vad avser storlek och massa. Vi kommer även att låta alla stötar vara helt elastiska dvs rörelsemängd och rörelseenergi bevaras (enkelt uttryckt så är varje partikel den ideala studsbollen). Även väggar, tak och golv kommer vara helt elastiska så ingen energi tillförs eller försvinner från systemet. Den simulator som vi har kan även visa grafiskt vad som händer vilket är rätt illustrativt men i de data som vi senare presenterar så är det statistik över hastighet mm i de olika lagren som vi kommer titta på. Simulatorn är inte världens snabbaste men klarar av att simulera tiotusen partiklar vilket är tillräckligt för våra ändamål.
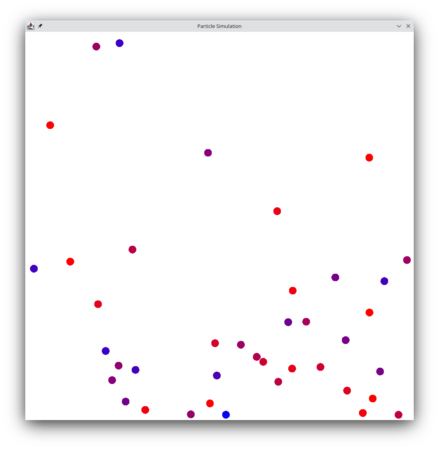
För den som vill bygga sin egen simulator kan jag nämna att detta är en s.k. händelsebaserad simulator (”discrete-event simulator”) vilket förenklar beräkningarna och gör det möjligt att simulera tusentals partiklar. Alternativet, och det man först skulle tänka på, är en tidsbaserad simulering. I en tidbaserad simulering låter tiden gå ett steg och räknar sen ut var alla partiklar befinner sig, ser om några har kolliderat och ändrar dess banor därefter. Denna metod är mycket tidsödande och öppnar upp för små fel som lätt fortplantar sig. Vid varje beräkning av en partikels nästa position så smyger det sig in ett avrundningsfel och efter hundra steg kanske vi inte alls är där vi skulle vara.
I en händelsebaserad simulering så räknar man istället ut vid vilken tidpunkt någonting eventuellt kan hända. Detta gör man helt enkelt genom att för varje par av partiklar undersöka om dessa kommer att krocka innan någon av dem träffar en vägg. Gör vi detta för alla par så kanske vi kommer fram till att ingenting kommer hända inom tjugo tidsenheter. Vi kan då tryggt ”hoppa fram” till denna tidpunkt och till exempel låta två partiklar krocka. Givet deras nya riktning så räknar man på nytt fram vilka nya händelser som skapats och lägger in dem i en händelskö.
Det enda komplicerade är att räkna ut om, och i så fall när, två partiklar kommer att kollidera. Hade vi inte haft gravitationen att ta hänsyn till så hade allt varit så enkelt som att dra två raka streck och räkna ut deras skärningspunkt men med gravitation så har vi ju två kastparabler att räkna på och det är inte riktigt lika enkelt … tills man gör ett litet tankeexperiment. Antag att du befinner dig svävande i en rymdkapsel någonstans i en galax långt, långt borta. Du har två kulor framför dig som rör sig mot varandra, kommer de att krocka och när? Ett enkelt överslag och två räta linjer ger dig resultatet, de kommer att krocka vid tidpunkt t. Antag nu att någon berättar för dig att du inte är med i Star Wars utan befinner dig i ISS i fritt fall runt jorden – skall du göra om dina beräkningar? Vet vi väl tidpunkten för kollisionen så är det enkelt att räkna på kastparabeln och se exakt var partiklarna kommer befinna sig.
Vårt första experiment
Vårt första experiment är så enkelt att vi skulle kunna räkna fram resultatet med penna och papper. Vi kommer ha ett rum på 1000×1000 och endast en partikel med en radie på 20 (om enheten är mm eller cm saknar betydelse, vi vet bara att det är gått om tomrum i simuleringen). Vi släpper vår enda partikel från höjden 480 och ger den en liten initial hastighet på 10 i horisontel riktning (längdenheter per tidenhet, tänk per sekund om det underlättar), gravitationen sätts till 10 (längdenheter per tidsenhet i kvadrat). Notera att vi inte håller på att efterlikna kvävemolekyler i atmosfären och det därför inte är viktigt att veta vilka enheter vi har för rymd och tid.
Vill man visualisera vad som kommer att hända så kommer vår partikel utföra perfekta studsar bort mot ena väggen där den vänder riktning och studsar mot rummets andra sida. Partikeln kommer vid höjden 480 ha en vertikal hastighet på 0 och en horisontell på 10. Ju längre ner mot golvet vi kommer får partikeln högre vertikal fart och slår i backen drygt nio sekunder med en fart på över nittio enheter per sekund.
Om vi vill ha lite statistik på vilken temperatur vi har vid olika höjder så kan vi ta lite ögonblicksbilder under simuleringen. Naturligtvis så är begreppet temperatur när vi bara har en partikel lite konstigt men det är väldefinierat vad vi menar. Vi tar en bild var tionde tidsenhet och summerar resultatet till en bild. Delar vi upp vår värld i tio nivåer får vi följande resultat:
4232, 3294, 2326, 1317, 300, NaN, NaN, NaN, NaN, NaN
Vi börjar vid golvet och går uppåt: temperaturen vid golvet är 4232, därefter 3294 och avtar sedan till 300 i skiktet mellan 400 och 500 höjenheter. Över den höjden har vi ingen temperatur eftersom vår partikel naturligtvis aldrig studsar högre än 480. Det vi ser är den gravito-termala effekten! Vi skulle kunna göra om experimentet med tusen partiklar från olika höjder och – så länge de inte krockar med varandra – skulle vi se hur den gravito-termala effekten ger oss en temperaturgradient.
Experiment nr två,
I nästa experiment gör vi en liten ändring, vi kastar in ytterligare en partikel. Den andra partikeln kommer släppas en bit ifrån den första från höjden 460 och med en vertikal hastighet på 10 riktat mot den första partikeln. Anledning till att vi släpper den från en liten annan höjd är att vi inte vill ha en helt symmetrisk utveckling där de två partiklarna bara är varandras spegelbilder. Vi borde naturligtvis få ett identiskt resultat men det konstiga är att utvecklingen skiljer sig rätt rejält:
3954, 3207, 1905, 1019, 672, 267, NaN, NaN, NaN, NaN,
Temperaturen närmast golvet har sjunkit en aning men det som är mest förvånande är att temperaturen har stigit mellan höjden 400 och 500 och att vi nu har en temperatur över höjden 500! När partiklar krockar så kan det mycket väl resultera i att en av partiklarna får en vertikal hastighet som ger den kraft nog att komma högre än någon av partiklarnas ursprungliga höjder. Vi ser fortfarande en gravito-termal effekt men vi har också sett varför den i det stora inte spelar någon roll.
… tre o fyra.
Låt oss se hur det ser ut med fyra eller åtta partiklar (alla släppta på en höjd mellan 460 och 480 och en liten vertikal hastighet). Vi börjar med fyra partiklar och tar ut mer statistik. Vid var tionde tidsenhet tar vi och räknar ut temperaturen vid de olika höjderna. Efter tio uträkningar gör vi en sammanställning som är en rad i utskriften nedan. Vi bygger där efter på med ytterligare tio ögonblicksbilder och rapporterar sedan den genomsnittliga temperaturen under hela förloppet igen. Detta repeterar vi sedan ytterligare åtta gånger och får då följande bild:
t: 0 NaN, NaN, NaN, NaN, 50, NaN, NaN, NaN, NaN, NaN, t: 1 4003, 2897, 2340, 1135, 237, NaN, NaN, NaN, NaN, NaN, t: 2 3740, 2941, 2182, 1333, 318, 1345, 1120, NaN, NaN, NaN, t: 3 3013, 2642, 2172, 1439, 574, 2075, 1120, NaN, NaN, NaN, t: 4 3137, 2261, 2139, 1631, 858, 2039, 1120, NaN, NaN, NaN, t: 5 3603, 2018, 2353, 1729, 905, 1665, 1120, NaN, NaN, NaN, t: 6 3469, 2155, 2212, 1831, 888, 1852, 1766, 1381, NaN, NaN, t: 7 3085, 2283, 2163, 1857, 989, 2244, 1805, 1381, 2601, NaN, t: 8 2913, 2382, 2161, 2034, 1163, 2231, 1702, 1725, 2601, 53, t: 9 2990, 2250, 2065, 1962, 1295, 2231, 1882, 1725, 1061, 27, t:10 3005, 2338, 2064, 2013, 1295, 2031, 1731, 1725, 1061, 27,
Notera hur vi från början inte har några partiklar på de högre höjderna men att vi sakta men säkert erövrar nivå efter nivå. Går vi upp till åtta partiklar så får ännu mer att tänka på, så här ser det ut efter ett tag:
t: 0 2784, 2719, 2653, 1995, 437, NaN, 1354, 111, NaN, NaN, t: 1 2803, 2439, 2508, 2345, 924, 1047, 1354, 1264, 1741, 338, t: 2 2943, 2339, 2107, 2698, 1245, 1123, 3346, 1264, 1741, 338, t: 3 2857, 2417, 2069, 2416, 1319, 1175, 2158, 1298, 1024, 338, t: 4 2669, 2495, 2131, 2439, 1464, 1270, 1723, 1298, 1024, 338, t: 5 2486, 2672, 2252, 2474, 1540, 1460, 1577, 1315, 1024, 338, t: 6 2375, 2672, 2321, 2555, 1634, 1327, 1577, 1313, 1024, 338, t: 7 2398, 2685, 2280, 2626, 1970, 1327, 1577, 1733, 924, 338, t: 8 2295, 2559, 2412, 2653, 2080, 1457, 2338, 1733, 1698, 2501, t: 9 2331, 2577, 2389, 2541, 2027, 1505, 2275, 1583, 1698, 2501,
Man börjar fundera över vart det här skall sluta, vi ser hur alla nivåer snabbt fylls upp men att det nu till och med är varmare ju högre upp vi kommer? Siffrorna för de högre lagren är dock rätt flyktiga eftersom få partiklar når upp till de höjderna och vi därför får en bild som är lite slumpartad. Skall vi få någon ordning på detta så skall vi nog göra körningar med tusentals partiklar och hålla på bra mycket längre än dessa experiment gjorde. Skall vi prova med hundra partiklar, tusen, eller varför inte tiotusen partiklar.
Titotusen röda rosor i ett fång
Vi drar igång en större simulering med höjden 10.000 och bredden 1.000. Vi släpper 10.000 partiklar med radien 1 från slumpade höjder 2.500 +/-1.250 med initial hastighet 0 (partiklar kommer hamna snett ovanför varandra och så snart de börjar kollidera så får vi all spridning vi behöver). Gravitationen sätts till 10 och vi delar som förut in vår yta i tio lager. Nedan en sekvens bilder där 1000 partiklar faller motmarken för att sedan börja studsa runt i ett rum på 1000×1000.
Vi kan titta på studsande partiklar i all evighet men det är statistiken vi vill åt. Istället för att titta på tabeller så kan vi göra lite diagram på hur temperaturen utvecklas på olika höjder allt eftersom simuleringen går framåt. Diagrammet nedan visar utvecklingen för medeltemperaturen för olika höjder i vårt rum.

Utvecklingen verkar lite kaosartad men har sin förklaring. Vid tidpunkt noll så ligger alla partiklar slumpvist utspridda runt höjden 2500. Temperaturen är initial 0 i segmentet 2000-3000 och obefintlig ( vi har inga partiklar ) vid övriga nivåer. När partiklarna faller nedåt så ökar temperaturen i den nedersta segmenten och efter en studs i golvet så sprider de sig uppåt. Till en början är det få partiklar som studsar så högt, men de som gör det har en hög hastighet och därmed temperatur. Vid tiden 15 (vilket motsvarar 150 tidsenheter i simuleringen) så börjar temperaturerna jämna ut sig det är svårt att se hur de olika nivåerna delar upp sig så vi tar en titt på hur det set ut efter tidpunkt 100.

Temperaturerna har planat ut men vi har en omvänd temperaturgradient. De övre lagren har en högre temperatur än de nedre lagren. Eftersom kurvorna visar den ackumulerade medelvärdet så är de i viss grad färgade av de tidigare höga temperaturerna men det finns en klar tendens till högre temperaturer i de tunnare lagren. För att Se hur stor skillnad det egentligen är när temperaturerna stabiliserat sig gjorde jag en simulering där vi hoppade fram tusen tidsenheter (dvs började där vår första simulering slutade) och tog sen medelvärdet under de följande tusen enheterna.
12415, 12406, 12430, 12430, 12407, 12385, 12378, 12390, 12719, 12211
Som synes så, förutom de två översta lagren, slår värdena på fjärde siffran dvs inte mycket tröst om vi letar efter en gravito-termal effekt. I den nedre halvan av rummet diffar temperaturerna på en tusendel vilket i sammanhanget är försumbart. Som jämförelse kan vi ta en partikel i den nedersta regionen med en temperatur, rörelse energi, på 12415, den har en hastighet på ca 157 enheter per tidsenhet. Låt oss anta att den har riktningen rakt upp och inte krockar med någonting på vägen upp så skulle den trots det aldrig slå i taket utan vända efter dryga 15 tidenheter på en höjd över 1200. Det är någonting som inte stämmer med teorin om den gravito-termala effekten men låt oss göra lite fler körningar.
hur förändras trycket
När vi ändå håller på så är det lätt att plocka ut statistik på hur trycket förändras på de olika nivåerna och där ser vi exakt vad vi kunde förvänta oss. Trycker stiger ju närmare golvet man kommer och vi har en exponentiell ökning. Anledningen till den exponentiella ökningen är att gas (till skillnad från t.ex. vätskor) är kompressibla och att ju närmare golvet vi kommer så finner vi ett lager med betydligt mycket mer partiklar är lagret ovanför. Den som dyker veta att vattentrycket ökar linjärt med ca 1 atm per tio meter men lufttrycket i atmosfären avtar alltså inte linjärt med höjden.

Diagrammet visar som förut det ackumulerade medelvärdet och vi ser att trycket på de olika höjderna stabiliserar sig relativt snabbt, redan efter 100 tidenheter har en jämvikt infunnit sig. Om vi jämför med troposfären så har vi vi jordytan ett lufttryck på ca 1 atm och vidd troposfärens högsta höjd, ca 10km, har vi ca 0.25 atm dvs en fjärdedel. I vår simulering skulle det innebära att troposfären slutade ungefär vid höjden 3000. För att få en bild av vad vi talar om så kan vi se hur de 10.000 partiklarna i medeltal fördelar sig mellan de olika höjderna:
5408, 2515, 1142, 516, 231, 104, 46, 20, 9, 4
Som synes har vi 50% i det första lagret och sen avtar antalet exponentiellt. Alla siffror vi har för de övre lagren kräver långa körningar om vi skall ha något statistiskt jämförbart.
Den simulering jag gör har inga anspråk på att modellera atmosfären och det kan ju vara så att den gravito-termala effekten inte infinner sig för just de värden jag valt så låt oss göra lite fler körningar.
Ändra på gravitationen
Vi gör om samma körning som ovan (nu till tidsenhet 2000) för olika värden på gravitationen: 1, 2, 4 och 8. Vi tar de slutliga medelvärdet för varje körning och redovisar det i en graf. De olika simuleringarna får olika temperaturer eftersom partiklarna släpps från samma höjd och att det med större gravitation ger högre potentiell energi som i slutändan resulterar i högre kinetisk energi. Vi ser dock ingen tillstymmelse till gravito-termal effekt men återigen ser vi en tendens till högre temperaturer på högre höjder.
Tunnare luft
Det kan ju vara så att vi har gjort våra simuleringar med för många partiklar och att vår gas är bra mycket tätare än luft. Det kanske finns en gravito-termal effekt som bara visar sig då avstånden mellan partiklar är tillräckligt stort. Jag gjorde därför fyra simuleringar där jag använde: 1000, 2000, 4000 och 8000 partiklar och gravitationen satt till 10 men inte heller där ser vi någon gravito-termal effekt. Jag kan inte förklara skillnaden i temperatur i de olika körningarna men den är så liten så att även den slumpmässiga initiala utspridningen kan spela roll.
De nedre lagren
Som en sista körning kan vi undersöka om en gravito-termal effekt gömmer sig i de nedre lagren. Det vi gjort hittills är kanske att titta på allt mellan jorden och stratosfären när effekten kanske bara återfinns i det som skulle motsvara troposfären. Vi gör en körning där gravitationen är satt till 10 och vi samplar statistik under 1000 tidenheter efter de första 1000 enheterna. Vi samplar dock bara information om den nedre fjärdedelen men bryter upp den i tio nivåer. Varje nivå motsvara nu 250 höjdenheter istället för1000. Som synes är skillnaden i de olika lagren marginell för att inte säga obetydlig.
12366, 12375, 12346, 12363, 12353, 12362, 12364, 12331, 12346, 12407
Skruva upp värmen
Vi kan försöka simulera vad som händer om vi har en varm jord som genom konduktion värmer upp det nedersta lagret av partiklar. Vid varje kollision med golvet ger vi den studsande partikeln en liten extra knuff. Hade vi kört en simulering rakt av så skulle vi sakta men säkert värma upp systemet men det skulle aldrig komma till ett stabilt läge eftersom vi bara tillsätter energi. Vi tar därför och inför ett iskallt tak där varje kolliderande partikel förlorar all sin energi för att sedan sakta falla mot marken. Sätter vi upp detta system ser vi hur varje lager får sin egen temperatur och systemet befinner sig efter ett tag i ett stabilt läge.

Den kaosartade utvecklingen i början är en effekt av att det initialt enbart är partiklar men hög hastighet som når upp till de högre höjderna. De nivåer som inte är inlagda ligger där de förväntas ligger dvs i mellanrummen mellan de kurvor som är inritade. Vi kan ta och rita upp temperaturgradienten och då också passa på att göra simuleringar med olika värden på gravitationen,
 Som synes så har gravitationen en stor inverkan på hur gradienten ser ut men kom nu ihåg att det är temperaturskillnaden mellan golv och tak som är orsaken till att vi överhuvudtaget har en gradient.
Som synes så har gravitationen en stor inverkan på hur gradienten ser ut men kom nu ihåg att det är temperaturskillnaden mellan golv och tak som är orsaken till att vi överhuvudtaget har en gradient.
För den analytiskt lagde
En simulering är rolig att göra men den räknas kanske inte som bevis. För den som gör simuleringen, i detta fall jag, räcker det dock som bevis och jag skulle bli mycket förvånad som den finns en gravito-termal effekt. För alla andra så är det till att lita på att jag programmerat rätt och att jag inte gjort antagande som inte stämmer. Ett analytiskt bevis skulle kanske vara mer övertygande men även där så blir det ofta en fråga om tilltro till den som presenterar beviset eftersom även bevis kan vara svåra att följa.
Det där får någon annan klura ut, jag är rätt övertygad om att den simulering jag gjort fångar allt och visar på att det inte finns någon gravito-termal effekt av betydelse.
P.S.
Det var ju ett tag sedan jag skrev några inlägg men är fortfarande övertygad, idag mer än någonsin, om att klimatkarusellen är en politisk cirkus om inte har så mycket med vetenskap att göra. Att jag här ställer mig tveksam till att det finns en gravito-termal effekt som Gösta Pettersson pekar på betyder inte att jag inte håller med Gösta i det mesta. Jag kan varmt rekommendera Falsk Alarm där Gösta gör en mycket bra genomgång av de vetenskapliga frågeställningarna (eller misstolkningarna) som ligger bakom klimathotet.

Lektor inom datakommunikation, KTH.
I <3 CO2 – Koldioxid är kanske inte världens viktigaste gas men den kommer som bra tvåa efter syre.













Intressant artikel. Ser fram emot ev. genlagor.
Det enda jag kan bidra med är påpekandet att vätskor visst är kompressibla, vatten t.ex är ungefär fyra gånger så elastiskt som stål. Om jag minns rätt.
Lite svårt att förstå hur trycket kan öka med djupet utan denna kompressibilitet.
Ber om ursäkt för denna OT.
#1 Dan
”… fyra gånger så elastiskt som stål.” Det är nog sant men i jämförelse med gaser så är det naturligtvis en västanfläkt. Jag hittade en siffra för vatten som minskar med 0.1% i volym vid hundra atmosfärers tryck.
Skillnaden mellan trycket i havet och i atmosfären är att eftersom vatten, i praktiken, inte trycks ihop – på de djup vi rör oss på – så kan man enkelt räkna med att trycket är linjärt i förhållande till djupet (1 atm / 10 m). I atmosfären så är skillnaden påtaglig och det är då vi får en exponentiell kurva.
Är man ute o vandrar i fjällen kan man dock räkna på en linjär skala ( 1 hPa / 8 m) när man skall koka sina ägg eftersom man inte förändrar sin höjd så mycket.
https://www.smhi.se/kunskapsbanken/meteorologi/lufttryck/lufttryck-1.657
Hoppsan, det ändrar hela min ’världsbild’ var min första reaktion. Men du beskriver två lösningar och det är inte självklart vilken som är riktig. Du beskriver inte varför gravito-termala effekten skulle vara felaktig och jag hittar inget skäl som kan bortförklara den.
Därför började jag söka fel i den statistiska metoden dvs dina simuleringar. Du tillför energi vid den understa studsen och tar bort lika mycket i den övre studsen. Men så ser inte verkligheten ut. Överföringen av energi från vattenytan till troposfären sker huvudsakligen med energirik vattenånga. Den energin omvandlas till strålning och/eller kinetisk energi när vattenångan kondenserar till vattendroppar dvs på de höjder där moln bildas. Någon ’knuffenergi’ från mark och vatten i nämnvärd mängd tillförs inte (tror jag) eftersom vattenytan håller ungefär samma temperatur som luftlagrens undre del.
Det måste rimligen vara något fel med simuleringen eller dess slutsatser. Beräknar du temperaturen som en funktion av farten i kvadrat?
–
Så ett skrivfel. ”höjden 480 och ger den en liten initial hastighet på 10 i vertikal riktning”. Så stod det på två ställen och du har nu ändrat det ena till ”horisontell” men det bör vara lika på båda ställena.
Välkommen tillbaka Johan och tack för en intressant simulering, ser fram emot dina välskrivna inlägg i framtiden.
#3 Lars Cornell
”Du beskriver inte varför gravito-termala effekten skulle vara felaktig och jag hittar inget skäl som kan bortförklara den. ”
Stämmer; jag pekar bara på att den inte visar sig när man gör en enkel simulering – där den borde visa sig.
”.. Men så ser inte verkligheten ut. ”
Helt riktigt men simuleringen där vi tillför energi vid golvet och plockar bort vid taket är bara ett exempel – det gör inget anspråk på att simulera hur atmosfären beter sig. Vi ser dock att vi i denna enkla modell direkt får en temperaturgradient (som också är beroende av gravitationen).
Vi kan egentligen bortse från simuleringen som inte är adiabatisk. Det jag funderar över varför vi inte ser någon gravito-termal effekt i det adiabatiska scenariot.
Temperaturen är hastigheten i kvadrat delat med två och jag har nagelfarit simuleringen eftersom det kommer bli väldigt pinsamt när det visar sig vara fel ( det är lite därför jag skriver inlägg – put my money where my mouth is
Jag är inte färdig att ge en analytisk förklaring till vad som händer men det är för mig helt klart att det har med kollisioner att göra. Så länge vi betraktar en partikel eller flera utan kollisioner så är allt enligt den gravito-termala teorin. När vi inför kollisioner så inträffar något – som jag pekar på när vi har två partiklar. Helt plötsligt så har vi titt som tätt en partikel på en höjd som är högre än den ursprungliga – varifrån fick den den energin? Den kan näppeligen fått den från någon ännu högre höjd utan det plockas naturligtvis från någon lägre höjd. Vi har en fördelning av rörelseenergin uppåt. Denna spridning av rörelsenergin kommer i slutändan att sudda ut den gravoto-termala effekten. Det är i alla fall hur jag tänker nu men någon statistiker med en syssloslös helg framför sig får klura ut vad det egentligen är som händer.
Tack för felet, skall fixa när är på rätt dator.
Tack Johan. Rolig att du är tillbaka.
”klimatkarusellen är en politisk cirkus som inte har så mycket med vetenskap att göra.”
Jag tror att alla med sunt förnuft kan instämma i detta uttalande.
Som icke-naturvetare har jag svårt att hänga med. Finns det kanske någon populärvetenskaplig förklaring? Johans engagemang gör mig nämligen synnerligen nyfiken.
Johan, suveränt pedagogiskt presenterat. Man skulle kunna jämföra exergin i ditt beräknade tillstånd för partiklarna med tillståndet om den gravito-termala effekten funnits och jämföra med termodynamikens andra huvudsats. Utan att räkna gissar jag att likformig temperatur stämmer med andra huvudsatsen. (Exergi definieras förenklat som mängden mekaniskt arbete som maximalt kan utvinnas ur ett system.)
Det som slår mig är att din simulering är att den är på atomnivå (molekylnivå) medans verklighetens atmosfär är på makroskopik nivå med konvektion som lyfter stora luftpaket som kyls och sedan sjunker. Dessa paket krockar inte med varandra utan lyfts intakta till en högnivå. På samma sätt sjunker stor luftpaket utan att krocka med andra paket.
I så fall skulle atmosfären representeras av den första simuleringen med en partikel eller liknande simuleringar där partiklarna inte krock med varandra och inte utbyter energi med varandra. År inte det som menas med adiabatisk process+
Lysande Johan! Man ska självklart undersöka saker själv.
Resultatet du har kommit fram till ligger helt i linje med vad jag själv har kommit fram till. Den gravito-termala effekten är bara en temporär effekt av att luften värms upp vi jordytan, som solen värmer, och kyls av på högre höjder med hjälp av växthusgaser. Den varma luften från jordytan stiger och beroende på hur varm luften är, dvs hur mycket energi den har, och hur stor gravitationen är så kommer luften att stiga olika högt. Men om man låter tiden gå utan att jordytan värms upp, så kommer så småningom luften genom värmeledning, dvs kollisioner, att ha samma temperatur på alla höjder.
Den temperatur-gradient vi observerar i verkligheten beror alltså på att konvektionen (värmeledning genom luftrörelser) är snabbare än värmeledningen (kollisioner). Men om jorden varken skulle ha växthusgaser eller tillförd energi från solen, skulle atmosfären ha samma temperatur på alla höjder.
Johan – Har jag förstått saken rätt?
Det skulle vara intressant att se hur temperaturgradienten närmast jordytan ändras om du ändrar gravitationen, (för simuleringen med tillförd energi nedtill och bortförd upptill).
#9 GoranA
Stämmer, men det är på partikelnivå vi skall se en gravito-termal effekt.
Att atmosfären har konvektion är en annan sak och där finns det en hel del som vi skall ta hänsyn till. Nedkylning och uppvärmning, som för t.ex föhnvindar, är en sak som vi skall ha koll på men i det fallet så sjunker temperaturen t.ex. för att luftpaketet expanderar och den energin tas från den termiska energin. Likaså ångbildning och kondensation av vatten som har en stor effekt. Alla dessa aspekter kommer dock som grädde på moset; den första frågan är om det finns en gravito-termal effekt – och den bör visa sig i en väldigt enkel modell.
#10 Magnus Cederlof
”Men om jorden varken skulle ha växthusgaser eller tillförd energi från solen, skulle atmosfären ha samma temperatur på alla höjder.”
Yep, det är min slutsats också. Man kan nog även säga att vi utan växthusgaser men med en sol skulle ha samma temperatur på alla höjder … om vi nu inte hade dag och natt och var på en rund jord På en platt jord med konstant sol skulle vi utan växthusgaser ha en och samma temperatur i hela atmosfären.
På en platt jord med konstant sol skulle vi utan växthusgaser ha en och samma temperatur i hela atmosfären.
Jag skall göra några extra körningar.
Väldigt intressant. Bra jobbat.
Hur ser du på pV= nRT ?
Kommer ej ihåg teorierna kring denna lag och ev begränsningar men du säger att trycket är högre nära marken vilket borde betyda en högre temperatur?
#7 Torsten Sandström
”Som icke-naturvetare har jag svårt att hänga med. Finns det kanske någon populärvetenskaplig förklaring? ”
Enligt termodynamikens andra sats kommer vid jämvikt i ett slutet system, där energiinnehållet är konstant, molekylrörelser och temperaturer att ställa in sig så att det inte längre kan utföra något arbete. Detta kan endast uppnås om temperaturen är konstant i hela behållaren.
#13 TorbjörnR
pV = nRT
är naturligtvis det som ger oss svaret på det mesta. Att trycket är högre vid lägre höjd där varje nivå har samma volym (eller area i vår simulering) beror antingen på att n är större eller att T är större. Det simuleringen visar att om vi bara har gravitation så kommer T att vara oförändrad i de olika nivåerna och det är alltså, som simuleringen visar, n som förändras.
I fallet där vi tillför energi vid golvet så har vi också en högre temperatur vilket gör att allt inte beror på n.
Det som citeras här kan ju inte vara sant: ”Antaget är att om den gravito-termala effekten finns i en tredimensionell värld så finns den i en tvådimensionell värld”. Det ända som existerar är det 3-dimensionella rummet. Är din simulering en spegling av rörelser i ett tänkt 3-dimensionellt koordinatsystem? Men då har vi ju också tre samtidiga speglingar eller projektioner av luftens molekyler i rummet. Vilket av dem? I övrigt så kan man nog inte avfärda den gravito-termala effekten så lätt.
Intressant, och kul att du är tillbaka som inläggsförfattare!
Har några funderingar:
1 – Om man har ett slutet rum där skillnaden i potentiell energi mellan golv och tak är relativt liten i förhållande till den kinteiska energi så säger termodynamik att det blir varmare vid taket.
Taket hindrar partiklarna att fördela sig enligt ekvipartitionsteoremet.
2 – jag har tolkat den s.k. termo-gravitala effekten som att deras förespråkare menar att den värmer jorden. Min bild är att gravitationen skapar temperaturgradienten, men att det inte har någon värmande effekt.
3 – det s.k. ekvipartitionsteoremet ger svaret på varför temperaturgradienten uppstår i ett gravitationsfält. Ekvipartitionsteoremet gäller för ett mångpartikelsystem i ett gravitationsfält.
Teoremet anänds för beräkning på stjärnor, men det gäller lika bra för vår atmosfär.
Ekvipartitionsteoremet säger att temperaturen ska sjunka med ca 7C/km, vilket stämmer skapligt med observationer.
4 – Atmosfären i sig har en värmande effekt (även utan växthusgaser). En tät atmosfär omfördelar värme över planeten. När man utjämnar en planets temperaturfördelning stiger temperaturen. Vid ”lokal” strålningsbalans (typ månen) blir det kallt. Flyttar man runt värmen så stiger medeltemperaturen, eftersom det hetaste områdena kyls ner. Hänger ihop med T^4 beroendet i Stefan Boltzmanns lag.
Tror att det är denna effekt som ligger bakom den effekt man ser av en tätare atmosfär.
För övrigt borde det ju gå väldigt lätt att verifiera den gravito-termala effekten experimentellt. Om man tar ett långt isolerat rör och ställer det upp. Blir det varmare längst ner eller inte? Nån borde ju ha gjort detta experiment.
#16 Björn
Vad skulle en tredimensionell värld tillföra? Jag kan förklara den gravito-termala effeten i en 2D-värld och man är helt övertygad om att den naturligtvis finns … tills man gör en simulering. Eller – säger du att den inte finns i en 2D-värld men i en 3D-värld?
Det är några rader kod att ändra simuleringen till 3D (om jag hoppar att göra en en snygg visualisering) och jag tror resultatet skulle vara det samma.
Bra !
Det är viktigt att diskutera alternativ till ”växthuseffekten”.
Om jag förstått rätt är den ” termo-gravitala effekten” detsamma som vi på Klimatsans kallat den ”Atmosfäriska Effekten”, ett uttryck som är lättare att förstå för gemene man:
https://klimatsans.com/2019/03/27/dr-hans-jelbring-om-den-atmosfariska-effekten/
#18 Magnus Cederlof
Jag tror att 1/ ingen har gjort det för att de flesta vet att det inte finns någon 2/ det är inte enkelt om man skall göra det med jordens gravitation, vi pratar om hundradels grader per meter och hur skall du se till så att ditt rör är helt isolerat mm.
Man skulle kunna göra ngt liknande med en centrifug men det är ialla fall små skillnader vi talar om.
#20 Sture Åström
Yep, verkar vara samma sak. Här är Jeldings artikel:
https://journals.sagepub.com/doi/10.1260/095830503765184655
bakom betalvägg
Hej Johan,
Jag har lite svårt att förstå vad det egentligen är du betvivlar på basis av dina simuleringar.
Du tycks mig acceptera att det föreligger ett gravito-termalt samband i form av den relation mellan luftmolekylers höjd och hastighet/temperatur som Loschmidt härledde och hänförde till en omvandling mellan kinetisk energi och lägesenergi (även dina partiklar rör sig i paraboliska ”kastbanor).
Men du tycks mig betvivla att detta samband ger upphov till en gravito-termal effekt i form av uppkomsten av en troposfärisk temperaturgradient med de av Loschmidt karakteriserade egenskaperna (linjärt avtagande temperaturer med en lapse rate som är proportionell mot gravitationskonstanten och kalkylerbar med kännedom om luftens värmekapacitet).
Bör det inte uppstå någon temperaturgradient enligt dina simuleringar? Eller bör gradienten ha andra egenskaper än de som Loschmidt beskrev som en gravito-termal effekt? Underkänner du Loschmidts förklaring till den empiriskt observerade gradientens existens och egenskaper med utgångspunkt från vad det gravito-termala sambandet bör medföra? Hur tycker du gradientens existens och egenskaper bättre kan förklaras?
Som jag skrev i mitt inlägg ”Den gravito-termala effekten” är Maxwell-Loschmidts förklaring till gradientens uppkomst och egenskaper välbefäst och allmänt accepterad, eftersom den rönt starkt stöd av såväl empiriska som teoretiska belägg. Inte minst av de beräkningar som man för mer än hundra år sen genomfört med statistisk-mekanistisk metodik rörande uppkomsten av temperaturgradienter på gravitationellt påverkade atmosfärer.
Die Gedanken sind frei, så man får tro eller betvivla vad man vill. Men vad mitt eget tänkande beträffar, så fäster jag betydligt mera vikt vid vad t. ex. Maxwell och Loschmidt anfört rörande den troposfäriska temperaturgradientens ursprung och egenskaper än vid de invändningar du på basis av dina simuleringar tycker dig kunna resa mot deras förklaringar.
Man kan ju jämföra med Venus, den sägs ju ha en extrem växthuseffekt. Men dock avtar temperaturen med höjden ungefär som på jorden. Ca 5 grader per km.
https://www.aeronomie.be/index.php/en/encyclopedia/venus-very-high-temperatures-day-and-night
Var kloden med en atmosfære uden drivhusgasser og uden tilført energi udefra, men med en indre energi med fx vulkansk opvarmning af jordytan, ville atmosfæren længst nede have jordytans høje temperatur, men længst oppe, nær verdensrummet, ville den have verdensrummets meget lave temperatur – der er en gradient. – Det samme hvis jordytan var opvarmet af Solen
#17 JonasW
1 – ”ekvipartitionsteoremet” – hmm, utanför mitt område men är inte detta en fördelning av rörelseenergin på hur många frihetsgrader en molekyl har att vibrera …?
Att det blir varmare längs taket i ett rum där vi inte har någon värmekälla tror jag inte på.
2. Jag tror de pekar på att den gradienten vi har till största del är en effekt av gravitationen. Den del som växthusgaserna sen bidrar med är mindre – och om vi då dubblar den effekten så är det inte hela världen. Min bild är att gravitationen i sig inte skapar någon gradient alls – däremot så bidrar den till dess utseende om vi genom uppvärmning och avkylning skapar en gradient.
3. som sagt utanför min kunskap men skall läsa på.
4. Håller med. I det fall vi faktiskt har en rund jord med dag och natt så har en atmosfär en stor betydelse och det är oavsett om det finns några växthusgaser eller inte (eller någon gravitation om vi bortser från att det inte skulle finnas så mycket atmosfär
”En teori är att temperaturskillnaden beror på växthusgaser, att luften värms upp på lägre höjd av strålning från jordytan och kyls av på högre höjder där strålningen kan gå rakt ut i rymden. Vet vi hur denna temperaturgradient ser ut kan vi naturligtvis räkna på hur den skulle se ut om vi fördubblade mängden växthusgaser.
Den andra teorin är den s.k. gravito-termala effekten; den säger att temperaturskillnaden är en naturlig följd av gravitationen. ”
Detta är felaktigt. Växthuseffekten påverkar temperaturen, men inte temperturgradienten, som bestäms av gravitationsfältets styrka och gasens specifika värme. Det är därför våtadiabaten är mindre än torradiabaten, eftersom vattenånga har större specifik värme än övriga atmosfärgaser.
Egentligen är ”lapse-rate” exakt samma fenomen som gör att en satellit i en elliptisk bana rör sig långsammare vid perigeum än i epigeum,
#tty27
Sammanfattningsvis tty, uppfattar jag dig rätt om du menar att såväl växthuseffekten ( okontroversiellt) som den gravitotermala ( kontroversiellt) finns?
#23 Gösta Pettersson
I den första simuleringen som jag gör där vi bara har en partikel så säger jag att vi här ser den gravito-termala effekten. Är vi överens om att det är en bra beskrivning av effekten?
Redan när vi inför två partiklar som kolliderar med varandra så får vi ett annat utfall. Titt som tätt så kommer en partikel att befinna sig över dess ursprungliga höjd. Är det vad man kan förvänta sig eller är det något fel i simuleringen?
När vi ökar antalet partiklar så ser vi hur den gravito-termala effekten avtar och när vi går upp til tusentals partiklar så kan vi inte längre påvisa den. Vill man hävda att gravitationen i sig skapar en temperaturgradient så hade vi sett en gradient i dessa simuleringar.
Det finns två alternativ 1/ simuleringen är visserligen korrekt men det finns en förklaring varför vi inte ser en temperatur gradient – och jag är mycket intresserad av att veta varför 2/ simuleringen är fel men om vi gjorde rätt så skulle vi se en gradient.
Så är det 1 eller 2 som gäller?
Säger du 2 så tror jag du har en uppförsbacke framför dig. Det är en väldigt enkel simulering i ett 2D-plan med uniforma partiklar.
#27 tty
”,,,men inte temperturgradienten, som bestäms av gravitationsfältets styrka”
Som mina simuleringar visar så påverkar gravitationen gradientens utseende men – att vi överhuvudtaget har en temperaturskillnad är inte pga gravitationen .. eller?
Det som (ofta) görs gällande är att temperaturskillnaden i sig till huvuddel – beror – på gravitationen. Det är det jag vill hävda inte är sant.
#24 Karl Eider
yep, … men är temperaturskillnaden – skapad – av gravitationen?
#25 Bjarne Bisballe
”..en atmosfære uden drivhusgasser …. ville den have verdensrummets meget lave temperatur ”
Varför då? Vad är det som skulle kyla av atmosfären vid högre höjder … konduktion? Vi kan inte ha konduktion mot en rymd som inte har någon massa. Den enda anledningen till att de högre lagren är kallare är att de kan – stråla ut – värme dvs de är växthusgaser. eller?
Lite youtube på fredagskvällen:
https://www.youtube.com/watch?v=2z5W6U6woaQ
Här är lite thermodynamik
https://www.smhi.se/kunskapsbanken/adiabatisk-1.28356
Johan Montelius [19]; Vi rör oss i en tredimensionell värld, där allting annat är teoretiskt. Det är ju därför som man nu rekommenderar att barn under 2 år inte skall ha tillgång till dataskärmar, just på grund av dessas 2-dimensionella karaktär. Du kan inte sträcka dig rumsligt efter något på en dataplatta, eller hur? Vår atmosfär går inte att beskriva i två dimensioner för någon sådan atmosfär existera ju inte. Den är komplex med sin rumsliga utbredning där en mängd fysikaliska fenomen både samverkar och motverkar. Kommer tiden också in, ökar komplexiteten ändå mer osv.
#34 Björn
Så i en tvådimensionell värld så existerar inte en gravito-termal effekt? …. eller?
Om den inte existerar i en tvådimensionell värld så förklara varför den skulle finnas i en tredimensionell värld.
Om den finns in en tvådimensionell värld så förklara varför den inte gör sig synlig i en simulering,
Det är viktigt att påpeka att atmosfären har en växthuseffekt, som gör att jordytan är varmare än vad som motsvaras av solens instrålning. Den här effekten uppstår när atmosfären strålar ut på ungefär 5 km höjd i snitt,och det finns en temperaturgradient i atmosfärens lägsta lager som gör att jordytan är 5 till 10 grader varmare per km (dvs 25 till 50 grader i detta exempel).
Temperaturgradienten uppkommer som en kombination solens instrålning, gravitationen och växthusgaserna. Storleken på gradienten beror dock främst på gravitationen och till viss del mängden vattenånga. Vattenånga innehåller mer energi än ”ren” luft och därför kan varm vattenånga stiga högre. Det gör att gradienten minskar. Ju högre gravitation, ju lägre kan varm luft stiga innan den kyls av, och då får man en högre gradient.
Eftersom jordens atmosfär i det lägsta lagret (troposfären) redan är till stor del mättad av växthusgaser (läs vattenånga), kommer en ökning av andelen växthusgaser att ge en väldigt liten effekt på temperaturen. Utstrålningen kommer fortfarande att ske på c:a 5km höjd (något slags mass-centrum i höjdled) och temperaturgradienten kommer på det stora hela att vara densamma. Det man pratar om är i sammanhanget oerhört små förändringar på någon grad.
Johan Montelius
#26 ”Min bild är att gravitationen i sig inte skapar någon gradient alls”
#30 ”Det som (ofta) görs gällande är att temperaturskillnaden i sig till huvuddel – beror – på gravitationen. Det är det jag vill hävda inte är sant.”
Och där jag (nu, liksom i tidigare meningsutbyten med dig) vill påpeka att det du hävdar står i strid med vad man (Loschmidt, Maxwell, Boltzmann m fl) redan under slutet av 1800-talet fann vara fallet på basis av mera övertygande argument och belägg än dina. Gradienten uppstår enligt nämnda lärda män eftersom den återspeglar det termodynamiskt stabila tillståndet för en gravitationspåverkad atmosfär med avseende på den höjdmässiga variationen av tillståndsvariabler som temperaturen och trycket. Bekräftat bl. a. av statistisk-mekaniska beräkningar av Maxwell-Boltzmann-fördelningar av t. ex. luftmolekylernas temperatur.
I en kommentar till ett tidigare inlägg om temperaturfördelningen i en adiabatisk cylinder utsatt för gravitation hade Johan M en referens till ett papper som stöder hans beräkningar d.v.s att det inte finns någon temperaturgradient.
https://tallbloke.files.wordpress.com/2012/01/coombes-laue.pdf
Gösta P #38,
Det hade varit intressant att veta vilka motargument du har emot Johans simuleringar. Att bara upprepa dina egna ståndpunkter ger inte så mycket nytt.
Vad är det för fel på Johans simuleringar? Det vore roligt med en riktig debatt.
#40 ”Det vore roligt med en riktig debatt.”
Om tvådimensionell massa?
#29 Johan Montelius
”Så är det 1 eller 2 som gäller? ”
Den för mig vettigaste beskrivningen är alternativ 2: ”simuleringen är fel men om vi gjorde rätt så skulle vi se en gradient.”
En för mig tveksam förutsättning i simuleringen är t. ex. att du förser 2D-behållaren med ett tak som får uppåtstigande partiklar att tvärvända och övergå till nedåtfallande på grund av en ”Maxwellsk demon” (taket) som säger ”hit upp, men inte högre”. Reellt finns inget tak, utan det är gravitationen som får partiklarna att återvända när deras rörelseenergi i uppåtriktning helt omvandlats till lägesenergi. Inför man ett tak som tvingar partiklarna att vända på lägre höjd än vad det det gravito-termala sambandet föreskriver, så kan det självfallet bli svårt att simulera fram en temperaturgradient som återger Loschmidts gravito-termala effekt.
Andra svårigheter med att genom simulering få en bild av vilka temperaturförhållanden som bör uppstå i ditt system rör vilka initialvärden man ska tilldela partiklarnas höjd, hastighet och temperatur, samt hur lång tid man ska simulera innan man kan anse sig ha nått termisk jämvikt. Men såna komplikationer är du medveten om.
Är du överens med Loschmidt om att det gravito-termala sambandet mellan kinetisk energi och lägesenergi existerar, så förvånar det mig att du väljer en så komplicerad metod som simulering för att undersöka vad sambandet bör leda till för temperaturförhållanden. Loschmidt använde sig av en betydligt direktare metod när han teoretiskt kvantifierade vilket resultat sambandet bör ge i form av den av honom karakteriserade troposfäriska temperaturgradienten. Vilken enligt hans av empiriska data stödda beskrivning representerar en gravito-termal effekt utan radiativa bidrag.
Samtidigt har jag full förståelse och respekt för din nyfikenhet och vilja att testa framlagda hypoteser på ditt eget sätt.
#40 Ingemar Nordin
Hoppas mitt svar i #42 till Johan är roligt nog.
#42 Gösta Pettersson
”Den för mig vettigaste beskrivningen är alternativ 2″
Det glädjer mig i det att vi då är överens om att vi borde se en gravito-termal effekt i ett tvådimensionellt system med uniforma elastiska partiklar. Så nu är frågan varför vi inte ser det.
” Reellt finns inget tak, utan det är gravitationen som får partiklarna att återvända …”
Ja det är en skillnad från verkligheten. frågan är dock om det har någon betydelse. För det första så är taket så högt upp att det är väldigt få partiklar som slår i taket. Jag listar i inlägget fördelningen av partiklar på de olika nivåerna och det var i medeltal bara 4 av tiotusen som befinner sig i det översta lagret.
Jag kan göra om simuleringen med en oändlig höjd och kan i samma veva ändra så att gravitationen sjunker med höjden (vilket jag ignorerar nu) och därmed införa en flykthastighet. Skulle det förändra saker?
Om vi ser på en partikel som idag studsar i taket och då direkt får en omvänd hastighet, vilken hastighet skulle den ha om den fick tid att vända på höjden tjugotusen? Den skulle naturligtvis ha samma hastighet nedåt när den passerar tiotusen.
Vi kommer naturligtvis ha en gravito-termal effekt på mycket höga höjder där partiklar är så få att de aldrig kolliderar med varandra. Det är dock inte detta som saken gäller, vi pratar om en temperturgradient i troposfären inte exosfären.
Roligt och uppfriskande att se Johan igen. Med ett resonemang jag som lekman nästan begriper. Utmanar min husgud Gösta Pettersson är ju spännande.
En fundering — såvitt jag förstår handlar din simulering om ”värmeledning”. Det jag tror mig ha förstått är att just värmeledning spelar väldigt liten roll i atmosfären, medan strömning är det som beskriver vår atmosfär bäst.
Hur simulerar man en atmosfär med luftpaket som stiger och sjunker. 3D stor area liten höjd?
#42 #44
Det jag reagerade på redan vid första genomläsningen är det sätt som molekylerna tillförs rummet. Med den metoden blir det mycket kallt så att de får svårt att nå högt. Hur förändras resultatet om molekylerna förs in med en hastighet som motsvarar ca 290° K på höjden noll?
Jag kan inte se något problem med att man sätter en vägg (spegel) uppåt såvida det inte förstorar något fel eller avrundning i beräkningarna. Men det har nog stor betydelse för simuleringen om golv och tak är elastiska (boll mot boll) eller robusta (boll mot stenvägg). Eller hur?
”För det första så är taket så högt upp att det är väldigt få partiklar som slår i taket”.
Det beror nog mer på att molekylerna är så orealistiskt kalla att de inte orkar flyga högt.
Ser man på diagrammen ”temperaturutveckling olika höjder” så finns det en intressant skillnad. Det är bara att ta fram förstoringsglaset och titta på kurvorna till höger. För att kunna jämföra med verkligheten måste man veta vad höjdnivåerna 1 – 10 motsvarar i m och vad temperatur 12 000 – 13 500 motsvarar i °K.
Om 13500 motsvarar 290 °K så blir 12000 lika med 258° dvs ca 30° lägre och det stämmer inte alltför illa med skillnaden mellan troposfärens nedre och övre skickt.
#37 MC
Även vid samma temperatur stiger vattenånga eftersom den är lättare (molekylvikt=18) än luft (molekylvikt=ca38).
Som jag skrev i #39 finns problemet som Johan har simulerat löst analytiskt både i det två- och tredimensionella fallet med samma resultat som Johan. Lösningen finns publicerad i Am. J. Phy. Vol. 53, No 3, 1985.
https://tallbloke.files.wordpress.com/2012/01/coombes-laue.pdf
Det stämmer ju också med det jag skrev i #14.
”Enligt termodynamikens andra sats kommer vid jämvikt i ett slutet system, där energiinnehållet är konstant, molekylrörelser och temperaturer att ställa in sig så att det inte längre kan utföra något arbete. Detta kan endast uppnås om temperaturen är konstant i hela behållaren.”
# fortsättning
Om temperaturen är konstant i behållaren är medelhastigheten hos molekylerna på varje nivå densamma, även i fallet med gravitation. Intuitivt kan man tycka att medelhastigheten minskar med höjden, som hastigheten gör för en enskild molekyl, som stiger uppåt, men det gör medelhastigheten inte för samtliga molekyler på en nivå. Matematiken är inte så enkel men den borde vara en njutbar läsning för Sten.
Johan Montelius [36]; Kanske lite sent ute, men en undran, hur man kan simulera rörelser i en gas utan att ta hänsyn till de olika molekylernas vikter, utbredning och kinetiska energi? Det är väl detta som saknas i datorsimuleringar och därför fås lika resultat oberoende av om denna simulering görs i 2D eller 3D.
#48 Bjerke. Länken ’coombes-laue’ var intressant och för mig revolutionerande – om slutsatsen är riktig. Dokumentet är pedagogiskt väl formulerat men jag har svårt att klara Maxwellmatematiken.
”The average kinetic energy of all molecules does not decrease with hight even through the kinetic energy of each individual molecule does decrease with hight.”
Förklara det begripligt den som kan.
#17 JonasW
Ber om ursäkt. Skrev fel!
Menade Virialteoremet, men jag skrev Ekvipartitionsteoremet.
Det ska vara Virialteoremet.
#46 Sten Kaijser
”.. din simulering om ”värmeledning” .. medan strömning är det som beskriver vår atmosfär bäst. ”
Så sant, men min avsikt är inte att göra en simulering som beskriver atmosfären på bästa möjliga sätt utan göra en så enkel model som möjligt där den s.k. gravito-termala effekten bör visa sig – vilket den sen inte gjorde.
Den gravito-termala effekten utalar sin om vad som alla kan vara överens om råder för en enskild partikel … och säger sen att detta medför att vi får en temperaturgradient. Simuleringen visar att så inte är fallet vilket är det besynnerliga.
Att atmosfären sen bäst beskrivs i termer av konvektion snararare än konduktion må vara sant men den gravito-termala effekten skall visa sig när vi gör en simulering på partikelnivå.
#47 Lars Cornell
”Med den metoden blir det mycket kallt så att de får svårt att nå högt. ”
Vad är högt? Jag tog till med höjden 10.000 för att vi inte skulle ha någon konstig effekt där ett tak införde någon konstig effekt. Gösta vill ta bort taket och göra en simulering utan tak eller med ett tak på 100.000 men du vill gärna ha ett lägre tak (eller öka temperaturen så att fler partiklar når upp till taket). Jag kan göra om simuleringarna men tror det det kommer göra någon skillnad? Jag visade hur det såg ut vid de nedre lagren (0 – 2500) vilket skulle kunna motsvara troposfären) men vi såg ingen temperaturgradient där.
”..golv och tak är elastiska..”
Alla kollisioner, partikel-partikel eller partikel-vägg, är helt elastiska. Ingen energi går förlorad.
”För att kunna jämföra med verkligheten måste man veta vad höjdnivåerna 1 – 10 motsvarar i m och vad temperatur 12 000 – 13 500 motsvarar i °K.”
U got a point – som amerikanerna säger. De enheter som jag änvänder är bara tagna ur luften – jag har inte försökt att återspegla verkliga förhållanden. Att jag valt gravitation till 10 är ju lite för att gravitationen vid jordytan är 9.8 m/s, höjden 10.000 skulle då kunna vara 10.000 m vilket är ok men hastigheten på partiklar stämmer so-so med verkligheten. Energi på 1200 motsvara en hastighet på 157 m/s vilket är en bit ifrån de ca 400 m/s som kvävemolekyler har vid jordytan.
Den stora skillnaden är dock kanske i tätheten. Jag gör en simulering där vi efter ett tag har ca 5000 partiklar på en yta av 1000×1000 (nedre segmentet) . Eftersom varje partikel har radien 1 så upptar de en yta av 1²*pi x 5.000 = 15.000 dvs 15% av ytan. Jag har inte räknat på kvävemolekylers storlek men kan tänka mig att de upptar en mindre volym (?).
Frågan är om vi måste efterlikna atmosfären. Den gravito-termala effekten är så enkel att den skall visa sig oavsett vilken gas vi väljer … eller?
#50 Björn
”… utan att ta hänsyn till de olika molekylernas vikter, utbredning och kinetiska energi?”
Den gravito-termala effekten, om den finns, bör visa sig även i en 2D-värld. Den skall också visa sig i en gas där alla molekyler väger exakt samma sak, och det kvittar vad de väger, och är exakt lika stora.
Så den simulering som görs är en simulering av den enklaste modell vi kan tänka oss – 2D, alla partiklar identiska, radie 1 och massa 1.
Det finns en ännu enklare simulering och det är i en 1D-värld dvs alla partiklar befinner sig direkt ovanför varandra på en rak linje. I den världen …. så finns den gravito-termala effekten! Dne kommer visa på samma resultat som vår 2D-simulering med enbart en partikel.
#52 JonasW
”Menade Virialteoremet, men jag skrev Ekvipartitionsteoremet.”
… shit, jag som just vet allt om ekvipartitionsteoremet … i alla fall hur man stavar till det
När man inte vet hur simuleringsprogrammet ser ut är det svårt att ha en uppfattning om det hela.
Molekylrörelser liknas ofta vid den brownska dynamiken, där molekylerna ständigt rör sig, kolliderar, byter riktning och utväxlar energi med varandra. Denna dynamik är karakteristisk för både gaser och vätskor, även när de verkar vara i fullständig stillhet eller jämvikt.
Denna konstanta rörelse av molekyler är också en grundläggande egenskap som återfinns i vädret och det molekylära maskineriet i våra celler.
Exempelvis påverkar den hur enzymer och DNA-molekyler beter sig inom cellerna. När det kommer till livet, är det viktigt att komma ihåg att jämvikt ofta associeras med stillastående, medan icke-jämviktstillstånd är det som karakteriserar livet, och jämvikt kan ses som lika med död.
Jag tenderar att tro att både den s.k. gravito-termala effekten och växthusgaserna påverkar temperaturgradienterna i troposfären. Dock verkar växthusgaserna, förutom vattenånga, ha en mindre inverkan på den globala temperaturen.
Det är alltså det samlade antalet faktorer som styr Jorden, och mänskligheten har endast en begränsad förståelse av dem.
Vår uppgift är att klokt anpassa oss till dessa förhållanden, men för närvarande verkar klokheten vara frånvarande.
#57 Adepten
”Jag tenderar att tro att både den s.k. gravito-termala effekten och växthusgaserna påverkar temperaturgradienterna i troposfären.”
Varför tror du det?
#56 Johan M
Min ursäkt om du slösat tid på ekvipartitionsteoremet.
Virialteoremet säger att den genomsnittliga kinetiska energin i ett mångpartikelsystem (typ en gas) är negativt kopplad till den potentiella energin.
Kinetisk energi = -1/2*Potentiell energi.
Den potentiella energin är mycket minus nära jordytan, och mindre minus en bit upp.
Den kinteiska energin måste alltså avta med ökande höjd.
Virialteoremet (som gäller allmänt för en gas) säger att temperaturen ska minska med höjden, på grund av gravitationen.
Har skrivit samma tugg flera gånger, men ändå .. det värde man får från virialteoremet är ca 7C/km.
Det värde man får från den adiabatiska approximationen är ca 9C/km.
Det man observerar är ca 6.5C/km.
#51 Lars Cornell
””The average kinetic energy of all molecules does not decrease with hight even through the kinetic energy of each individual molecule does decrease with hight.”
Förklara det begripligt den som kan.”
I Johans värld har de flesta kommentarerna gällt molekylernas hastighet (=temperatur) och deras höjd i ett gravitationsfällt (=lägesenergi) men inte så ofta trycket, jämför pV =nRT. Skälet att medelhastigheten är densamma på alla nivåer i Johans värld är att ändringen i lägesenergi övergår till ett ökande eller minskande tryck.
#58 Johan M
Enkelt uttryckt utan diagram och ekvationer blir svaret att:
1) Växthuseffekten handlar om hur vissa gaser i atmosfären, som koldioxid och vattenånga, fångar upp och återutstrålar värme från jorden. Dessa gaser agerar som ett täcke och bidrar till att hålla kvar värme, vilket gör att jordens yta blir varmare än den skulle vara utan dessa gaser.
2) Gravito-termala effekten som inte är inte lika välkänd och är kopplad till tyngdkraften och atmosfären. När luften värms upp vid markytan, blir den lättare och stiger uppåt på grund av markutstrålningen resp. tyngdkraften. När den stiger, svalnar den och sprider sig i atmosfären. Detta skapar en cirkulation där varm luft stiger och kall luft sjunker, vilket påverkar klimatet och vädret.
Så, i korthet, växthuseffekten handlar om värmehållning genom vissa gaser, medan gravito-termala effekten handlar om cirkulation och rörelse av luft i atmosfären på grund av temperaturvariationer och tyngdkraft..
#15 Johan M
”pV = nRT
är naturligtvis det som ger oss svaret på det mesta. Att trycket är högre vid lägre höjd där varje nivå har samma volym (eller area i vår simulering) beror antingen på att n är större eller att T är större. Det simuleringen visar att om vi bara har gravitation så kommer T att vara oförändrad i de olika nivåerna och det är alltså, som simuleringen visar, n som förändras.”
Jag vill formulera detta så, att då eneriinnehållet och temperaturen i din modell är konstant, kommer den högre lägesenergin i de övre skikten att motsvaras av högre tryckenergi i de lägre skikten.
#23 Gösta Petterson
”Du tycks mig acceptera att det föreligger ett gravito-termalt samband i form av den relation mellan luftmolekylers höjd och hastighet/temperatur som Loschmidt härledde och hänförde till en omvandling mellan kinetisk energi och lägesenergi-”
Varför skriver du inte ……mellan kinetisk energi, lägesenergi och tryckenergi? Gäller inte omvandlingen till tryckenergi i det icke-adiabatiska fallet?
#63 Lars-Eric Bjerke
”Varför skriver du inte ……mellan kinetisk energi, lägesenergi och tryckenergi?”
Därför att Loschmidt endast intresserade sig för höjdberoendet av temperaturen (kinetisk energi) när han härledde sin ekvation för den gravito-termala temperaturgradienten. Gravitationens effekt på höjdberoendet av trycket utreddes av Maxwell när han (1871 vill jag minnas) härledde sin barometerformel.
Loschmidts temperaturgradient och Maxwells barometerformel är två sidor av samma mynt. Den ena sambandet kan härledas från det andra genom att utnyttja allmänna gaslagens uttryck för sambandet mellan temperatur och tryck.
#48 Lars-Eric Bjerke
”Som jag skrev i #39 finns problemet som Johan har simulerat löst analytiskt”
#49 Lars-Eric Bjerke
”Matematiken är inte så enkel ”
Nej, matematiken i arbetet av Coombes-Laue är inte enkel. Den är inte ens sund. Arbetet kan inte betraktas som en analytisk lösning till det problem som Johan söker lösa med sina simuleringar. Förklaringen varför ger jag i min efterföljande kommentar till Lars Cornell.
#51 Lars Cornell
” ”The average kinetic energy of all molecules does not decrease with hight even through the kinetic energy of each individual molecule does decrease with hight.”
Förklara det begripligt den som kan.”
Jag kan begripligt förklara vad Coombes-Laue hävdar, nämligen att den genomsnittliga kinetiska energin (dvs temperaturen) är höjdoberoende, trots att den kinetiska energin för varje individuell molekyl minskar med höjden. Däremot är det obegripligt att författarna inte inser hur orimlig deras slutsats är.
Matematiskt förklarar man att slutsatsen följer från den i arbetet härledda Ekv (7), enligt ett tänkande som specificeras i Appendix och med Lars-Eric Bjerkes ord i #49 inte är så enkelt att förstå. Samtidigt förklarar man att Ekv (7) efter lite algebra även leder fram till barometerformeln. Det senare tror jag är korrekt, och då har man också visat att det föreligger en temperaturgradient (gradienten och barometerformeln är två sidor av samma mynt, som jag påpekade i min kommentar #64,
Med andra ord, Coombes-Laue har inte presenterat några matematiskt hållbara belägg för att troposfären är isoterm, utan snarare befäst att det måste uppkomma en temperaturgradient. Jag kan överhuvud taget inte förstå hur någon på fullt allvar beaktar möjligheten att troposfären är isoterm när vi sedan länge kunnat empiriskt konstatera att den uppvisar en temperaturgradient.
# Johan Montelius
Förändras simuleringen möjligen om du lägger in att golv och tak är krökta samt att väggarna i boxen lutar utåt?
Det finns ju en ”geometrisk” expansion med ökande höjd
#61 Adepten
”… medan gravito-termala effekten handlar om cirkulation och rörelse av luft i atmosfären på grund av temperaturvariationer.”
Nej, den gravito-termal effekten finns oberoende av konvektion och har ingenting med temperaturvariationer att göra,
#67 Hans H m.fl
Flera kommentarer föreslår att vi ändrar några parametrar i simuleringen för att se om det gör någon skillnad och det är naturligtvis ett vettigt förslag. Jag gjorde själv flera olika körningar där jag varierade gravitation, tillförde värme mm. Frågan är kanske om det är rätt väg att gå.
Den vetenskapliga vägen när man vill pröva en teori är att göra en förutsägelse om hur världen kommer att utvecklas i ett experiment, utföra experimentet …. och sen finna sig i resultatet.
Richard Feynman
https://www.youtube.com/watch?v=EYPapE-3FRw&list=PLyQSN7X0ro23NUN9RYBP5xdBYoiv2_5y2
”If it disagrees with experiments, it’s wrong”
Hmm, säger nu de flesta – du har ju inte gjort ett experiment, det är ju bara en simulering. Stämmer, men vad är skillnaden?
Gör jag ett experiment så kommer jag att stå inför hundra problem att lösa, stor silo med gas som är helt isolerad från omvärlden, mätnoggrannhet av temperatur på hundradels grader mm. När jag är klar kommer någon att påpeka att silon bara var 10 m hög och att den nog borde vara 300 m, att det fanns lite fukt i silon mm – det är inte enkelt alla gånger.
En simulering är ett idealiserat experiment. Vill jag ha en isolerar silo så skapar jag en perfekt isolerad silo. Skall den vara tusen meter hör så skapar jag den tusen meter hög. Jag bestämmer exakt hur världen ser ut.
Kan vi då alltid använda en simulering istället för ett experiment. Nej – i de flesta fall är kunskapen om världen begränsad så min modell som jag vill simulera kommer att vara allt för enkel för att motsvara verkligheten. Men – ibland är det så att en simulering kan göra ett bättre jobb än ett experiment och jag vill hävda att vi har att göra med ett sådant fall.
Den gravito-termal effekten är väldigt enkel och den skall finnas i en väldigt enkel värld. Låt oss konstruera den enklaste världen vi kan och med hjälp av teorin göra en förutsägelse. Är världen enkel så blir simuleringen enkel och vi kan utföra experimentet.
Antag att vi har ett 2D rum 1000mx1000m stor där vi kastar in 1000 identiska partiklar. Elastiska stötar, adiabatiskt och ingen gravitation. Jag tror att alla kommer vara överens om att vi efter ett tag kommer ha samma temperatur t K på alla nivåer i rummet.
Slå nu på en gravitation g som är uniform i hela rummet. Vi räknar inte med gravitationen mellan partiklar.
Vad säger den gravito-termala teorin nu kommer hända? Ge värden på T och g och ge en förutsägelse om temperaturgradienten. Kan teorin inte ge en förutsägelse så är det inte en teori.
När vi väl är klara med hur modellen skall se ut och gjort vår förutsägelse så kan vi utföra ”experimentet”.
#60 Bjerke. ”att ändringen i lägesenergi övergår till ett ökande eller minskande tryck.”
NEJ! ”två sidor av samma mynt” som G.P uttrycker det.
#62 Bjerke ”… kommer den högre lägesenergin i de övre skikten att motsvaras av högre tryckenergi i de lägre skikten.” Nej. ”Tryckenergi” vad är det?
En molekyl på 10 km höjd har annan lägesenergi än en annan lika dan molekyl på 20 km höjd. Men båda påverkar trycket på underliggande gasmassa lika mycket, inte på grund av sin lägesenergi utan på grund av sin massa och gravitationen. Massa * gravitation ger en kraft men ger inte energi.
Om man släpper en molekyl fritt från 10 000 meters höjd kommer den att nå en hastighet av ca 440 m/s. Vilken temperatur detta motsvarar får man ur formeln
v = (3RT/m)^0,5
där v är molekylhastigheten i m/s, R är den ideala gaskonstanten (8,314), T temperaturen i K och m massan av en mol av den aktuella gasen i kg.
Påpekas bör att, i genomsnitt är den fria vägen innan en molekyl kolliderar med en annan ungefär en tiotusendels millimeter. /Citat från tty, avkortat.
Som du ser Bjerke ingår inte luftmassans tryck i formeln.
#67 Hans H.
Volymens form borde inte ha någon inverkan, den skulle tom kunna vara rund. Men du har en poäng, om formen har betydelse så indikerar det ett fel i simuleringsmodellen.
Hur ser den elastiska kollisionen vid tak och vägg ut? Är det som om en biljardboll i rörelse kolliderar med en stillastående biljardboll. Eller är det som om en biljardboll kolliderar med en bergvägg? Båda fallen är elastiska och utan energiförlust men ger ändå helt olika resultat.
#Montelius. I ett fall för du in energi i botten och tar bort motsvarande i toppen, du rubbar jämvikten. Det är intressant och visar gasmassans isolerande egenskap. Men är det så vårt ’problem’ ser ut?
#69 Hur bär du dig åt för att påstå att molekylernas fart högt upp är mindre än vid jordytan (om det tycks enighet råda) men att det inte påverkar temperaturen i din simulering?
#66 Gösta Pettersson
Tack, nu blev livet lättare att leva.
#68 Johan M
”Nej, den gravito-termal effekten finns oberoende av konvektion och har ingenting med temperaturvariationer att göra,”
Kan du förklara skillnaden mellan gravito-temal effekt och konvektion?
Oj vad mycket jag inte förstår.
Hur kan en2D värld plötsligt få ett tak. Då blir det ju 3D värld.
Men kul är det att läsa.
#71 Adepten
Den gravito-termala effekten är en effekt på partikelnivå … som sägs ge en effekt på macronivå. Den gravito-termala effekten skall ge en temperaturgradient i ett rum utan konvektion. Den gravito-termala effekten verkar genom konduktion.
Vad är konvektion? Ett fenomen på macronivå där skillnader i tryck (densitet) får stor luft (eller vatten) massor att sättas i rörelse. Det är i huvudsak det som händer i vår atmosfär (eller hav. Har du ett slutet rum utan värmekälla/avkylning så kommer du inte ha någon konvektion.
Adepten #71. Skillnaden består i att det inte finns någon likhet.
#72 Bim
Du kan välja mellan: fyra väggar eller två väggar, ”tak” och ”golv”. Vad vill du kalla dem?
#70 Lars Cornell
”I ett fall för du in energi i botten … är det så vårt ’problem’ ser ut?”
Nej, det bara ett exempel på hur vi överhuvudtaget skulle får en temperaturgradient. För att utröna om den gravito-termala effekten ger oss en gradient i sig så räcker det med de första experimenten där vi har ett adiabatiskt system. Ser vi ingen där så finns den inte. Att gravitationen sedan påverkar en gradient som vi fått genom att ha ett varmt golv och ett kallt tak är en annan sak.
Vi skulle, om det var det vi var ute efter, försöka simulera strålning från golvet och hur våra partiklar tar upp och avger den i alla riktningar men som sagt det är inte växthuseffekten vi försöker simulera utan frågan om den gravito-termala effekten finns.
#70 Lars Cornell
”#69 Hur bär du dig åt för att påstå att molekylernas fart högt upp är mindre än vid jordytan (om det tycks enighet råda) men att det inte påverkar temperaturen i din simulering? ”
…? Nu ser jag inte vad du menar. I #69 så säger jag att vi nog är överens om att vid avsaknad av gravitation så kommer temperaturen efter ett tag vara lika på alla nivåer.
De simuleringar jag gör visar att även då vi slår på gravitationen så kommer temperaturen att vara oförändrad (trycket kommer dock att ändras).
#70 Lars Cornell
”Är det som om en biljardboll i rörelse kolliderar med en stillastående biljardboll. Eller är det som om en biljardboll kolliderar med en bergvägg? ”
Som en bergvägg, partikeln bibehåller all rörelseenergi.
#70 Lars Cornell
” Bjerke ”… kommer den högre lägesenergin i i de övre skikten att motsvaras av högre tryckenergi i de lägre skikten.” Nej. ”Tryckenergi” vad är det?”
Det är den energi som krävs för att kulorna ska förtätas och ge större tryck (flera kollisioner med) på det adiabatiska kärlets väggar.
Tryck kan helt omvandlas till arbete till skillnad från temperatur. Det är därför som jämviktstillståndet i ett adiabatiskt kärl med eller utan gravitation blir likformig temperatur, vilket är ett gott indicium för att Johan har gjort en korrekt modellering av förhållandena i ett adiabatiskt kärl.
#74 veritas
Ha Det var en underfundig formulering som inte gjorde mig klokare
Det var en underfundig formulering som inte gjorde mig klokare
Men du kan kanske förklara likheterna med gravito-termal effekt och konvektion?
#80 Adepten
se #73, är det ett svar?
Så här säger SMHI.
”I nedre delen av atmosfären blandas luft från olika nivåer och därvid avkyls luft som förs uppåt,medan luft som förs nedåt värms upp.
Detta beror på att lufttrycket avtar med höjden, vilket leder till att ett luftpaket som stiger uppåt kommer att utvidgas, vilket leder till att dess temperatur avtar”
#82 Jan-Åke. Jag har också läst det som SMHI skriver. De gör det lätt för sig, men är det rätt?
#81 Johan M
Javisst ett bra svar
Jag tänkte så här att gravitationen och densitetsskillnader spelar en central roll i både gravitotermala effekter och konvektion, som båda påverkar luftcirkulationen.
Dessa fenomen är kopplade genom hur uppvärmning och densitetsvariationer initierar rörelse i atmosfären på olika skalor, från övergripande cirkulationsmönster till lokala konvektiva processer.
Är den här rapporten, Temperaturgradient för vertikal luftpelare i gravitationsfältet, ett exempel som stödjer din och Göstas uppfattning om gravito-termal effekten?
https://www.nature.com/articles/s41598-022-10525-0
Hej Johan!
När jag börjar läsa ditt inlägg ser jag några påståenden som enligt min uppfattning inte stämmer.
1)Gösta Pettersson har i flera inlägg pekat på att den den s.k. gravito-termala effekten är huvudorsak till den temperaturgradient vi ser i troposfären och att den effekt som tillskrivs växthusgaserna därmed är överdriven. Såvitt mig bekant är växthusgaserna inte alls en bidragande faktor till den temperaturgradient vi ser i troposfären.
2) En teori är att temperaturskillnaden beror på växthusgaser, att luften värms upp på lägre höjd av strålning från jordytan och kyls av på högre höjder där strålningen kan gå rakt ut i rymden. Vet vi hur denna temperaturgradient ser ut kan vi naturligtvis räkna på hur den skulle se ut om vi fördubblade mängden växthusgaser. Varifrån kommer denna teori? Såvitt mig bekant finns inga förespråkare för den. Den teori som är allmänt använd går ut på att atmosfären tillförs energi på alla höjder av olika skäl. Strålning från solen, strålning från såväl underliggande som överliggande luftlager, och omvandling mellan vattnets faser. Nettot av dessa ger uppvärmning eller avkylning. Det spelar ingen roll på vilken höjd uppvärmningen av troposfären sker på grund av den höga omblandningen i troposfären. Det är konvektionen som upprätthåller den gravito-termala effekten.
3)Den gravito-termala effekten är inte beroende av några konstiga parametrar som vi måste gissa, atmosfärens sammansättning eller jordens krökning – den finns i en tvådimensionell värld med identiska partiklar och fullständigt elastiska stötar….. och detta är väldigt enkelt att simulera. I simuleringen finns inte möjligheten för luftmassor med olika temperatur. Jag vill föreslå ett par tankeexperiment som kanske kan ge uppslag till en mer realistisk simulering.
a) Tänk en stillastående, icke roterande, jord som hålls vid 290K över hela ytan med en underliggande värmekälla. Den svävar fritt i Universum och har en atmosfär av ren kvävgas. Den kommer att stråla som svartkropp från ytan som kan ha ett albedo 0,95 över hela IR-spektrum. Jag tror att en sådan planet skulle få en stillastående atmosfär och därmed sakna temperaturgradient.
b) Tänk en roterande planet med atmosfär av ren kvävgas som befinner sig på ett avstånd från solen som ger en global genomsnittstemperatur av 255K. Temperaturen vid polerna skulle vara mycket lägre än temperaturen vid ekvatorn. Såvitt jag kan förstå skulle det uppstå kraftig luftcirkulation som skulle föra värme från ekvatorn mot polerna. Därvid skulle också vertikala luftrörelser uppstå. All strålning skulle komma från ytan men med olika intensitet vid olika latituder och årstider. Jag tror att en sådan planet skulle ha en temperaturgradient i enlighet med den gravito-termala effekten.
c) Tänk planeten enligt b) där vi ändrat sammansättningen av atmosfären till 99% kvävgas och 1% koldioxid. Atmosfären skulle absorbera och avge strålning vid koldioxidens resonanser. Det skulle förändra det spektrum som kan observeras från rymden signifikant. Inom området 640 till 700 cm-1 skulle strålningen bli mycket svagare. Koldioxiden är helt ogenomskinlig upp till cirka 6 km höjd så strålning från jordatmosfärens koldioxid kan inte nå universum från lägre höjd än så. Därmed blir intensiteten mycket lägre, den är ju proportionell mot T^4 och atmosfär under turbulent omrörning upprätthåller laps rate i enlighet med den gravito-termala effekten. Den totalt utgående strålningen måste vara i balans med den ingående och den svagare strålningen inom koldioxidens absorptionsband måste kompenseras med en högre marktemperatur.
Kanske skulle den tvådimensionella simuleringen ge en vertikal temperaturgradient ifall du inför såväl en värmekälla som en värmesänka i golvet. Ett slumpmässigt rörelsemängdstillskott vars amplitud varierar från +1 vid ena kanten (värme) till -1 vid motsatta kanten (kyla). Skulle inkommande rörelseenergi vara för liten för att räcka till någon rörelse alls efter subtraktionen på den kylande sidan får energiskillnaden sparas och användas till att ge andra partiklar svagare kylning. Med en sådan simulering borde en vertikal konvektion kunna iakttagas och med den kanske den gravito-termala effekten.
Jag hittade denna intressanta artikel som påstår att 2 parametrar huvudsakligen styr jordens temperatur och att jorden har kraftig negativ feedback som håller klimatet någorlunda konstant.
Parametrarna är
TOA irradiance
Atmosfärens totala tryck
Känns väldigt mycket kopplat till GPs atmosfäriska effekt och att växthusgaser har liten påverkan annat än att stråla ut värme.
Det intressanta är att de påstår att atmosfärens effekt är 90 K isf det normala 33 K.
Någon intelligent kommentar kring detta?
https://www.omicsonline.org/open-access/new-insights-on-the-physical-nature-of-the-atmospheric-greenhouse-effect-deduced-from-an-empirical-planetary-temperature-model.php?aid=88574&fbclid=IwAR3JNyzXxj0Zjrrn1_38Lh0dIXguPqoHIriz1kqPvScgqG4dChCBOdJiYIc_aem_AeDrs24E-PI0l4qx3uhahskNEHAEqfAhHp2RGJM8soPTzZ5Nka_XApqGAEGp5dyV9H4
#85 Leif Åsbrink
1/ ”Såvitt mig bekant är växthusgaserna inte alls en bidragande faktor till den temperaturgradient vi ser i troposfären.”
Jasså, vad grundar du det på?
2/ ”Det är konvektionen som upprätthåller den gravito-termala effekten.”
ok, så nu är den gravito-ternala effekten, som kan förklara med gravitationes påverkan på en enstaka partikel helt plötsligt beroende av konvektion? Jag tror vi har helt olika uppfattningar om vad som menas med gravito-termal effekt.
3/ ”I simuleringen finns inte möjligheten för luftmassor med olika temperatur. ” Varför då?
”Jag tror att en sådan planet skulle få en stillastående atmosfär och därmed sakna temperaturgradient.”
Den stämmer med vad jag anser men det anser inte de som hävdar att det finns en gravito-termal effekt. De säger att vi kommer ha en gradient.
”…. Jag tror att en sådan planet skulle ha en temperaturgradient i enlighet med den gravito-termala effekten.”
Det skulle den säkert men inte på grund av någon gravito-termal effekt.
”Kanske skulle den tvådimensionella simuleringen ge en vertikal temperaturgradient ifall du inför såväl en värmekälla som en värmesänka i golvet.”
Kanske det kanske, men nu är inte fråga hur vi kan skapa en gradient utan varför det inte finns en gradient i en värld med bara gravitation och ingen värmekälla.
”Med en sådan simulering borde en vertikal konvektion kunna iakttagas och med den kanske den gravito-termala effekten.”
Som sagt – den gravito-termal effekten skall vara synlig utan någon konvektion.
#84 Adepten
”Jag tänkte så här att gravitationen och densitetsskillnader spelar en central roll i både gravitotermala effekter och konvektion,”
Nej, gravitation spelar den enda rollen i den gravito-termala effekten, gravitation och densitet spelar en roll i konvektion.
Separera dessa saker.
#44 Johan Montelius
”Det glädjer mig i det att vi då är överens om att vi borde se en gravito-termal effekt i ett tvådimensionellt system med uniforma elastiska partiklar. Så nu är frågan varför vi inte ser det.”
Kommer strax tillbaka till den frågan. Men som jag skrev i #38 invänder jag främst mot din slutsats i #26 att gravitationen i sig inte skapar någon gradient och andra uttalanden där du säger dig betvivla att det finns någon gravito-termal effekt och därmed underkänner Loschmidts förklaring till den troposfäriska temperaturgradientens uppkomst och karakteristika.
Så här sa Loschmidt: En luftmolekyls totala energi (U) ges av U = cp T + g m h, dvs av dess kinetiska energi + dess lägesenergi. Rör molekylen sig i vertikal riktning, så sker det en omvandling mellan kinetisk energi och lägesenergi. Det utgör ett gravito-termalt samband som alltid måste gälla och som därmed också måste ge upphov till en gravito-termal effekt. Loschmidt beskrev effekten genom derivering av sambandet, vilket gav dT/dh = –g m/cp. Det uppstår en temperaturgradient där temperaturerna avtar linjärt med öknande höjd och en lapse rate som är proportionell mot gravitationskonstanten och beräkningsbar.
Loschmidts beskrivning av denna gravito-termala effekt är allmänt accepterad eftersom den ger en utmärkt förklaring till den gradient som empiriskt har observerats. Dina simuleringar ger resultat som inte stämmer överens med vad som observerats. Då tycks det mig obefogad att ifrågasätta Loschmidts förklaring (han lyckades beskriva verkligheten, det gjorde inte du). Det är av den anledningen jag valde ditt alternativ 2, dvs. att det måste vara fel på dina simuleringar.
Och då kommer vi till frågan varför du inte ser någon gravito-termal effekt i dina simuleringar. Där jag inte har något svar att ge utöver vad jag anförde i #42. Jag har stor tilltro till din förmåga att genomföra tekniskt korrekta simuleringar. Men för säkerhets skull måste jag ändå fråga dig om partiklarna i dina system uppfyller det grundläggande gravito-termala sambandet U = cp T + g m h eller dess motsvarighet.
#87 Johan Montelius
”1/ ”Såvitt mig bekant är växthusgaserna inte alls en bidragande faktor till den temperaturgradient vi ser i troposfären.”
Jasså, vad grundar du det på?”
Eftersom Leif ännu inte svarat på den frågan tillåter jag mig att förmoda att han som anhängare av Loschmidts förklaring kommer att hänvisa till ekvationen dT/dh = –g m/cp ovan, vilken beskriver gradienten som en ren gravitationseffekt utan radiativa bidrag.
#85 Leif Åsbrink
”3a) Jag tror att en sådan planet skulle få en stillastående atmosfär och därmed sakna temperaturgradient.”
Jag håller ovanligt nog med dig om nästan allt av vad du säger. Men beträffande tänkta planeter med en atmosfär av till exempel ren kvävgas eller ren syrgas så ha man inom statistisk mekanik funnit att även dessa kommer att utbilda en Loschmidtsk temperaturgradient. Det grundläggande gravito-termala sambandet U = cp T + g m h gäller även i sådana fall och anses ge upphov till en gradient på grund av gasmolekylernas ”egenrörelse” hitan och ditan. Det krävs ingen konvektion.
Enligt Maxwell strävar luften i troposfären mot det termodynamiskt stabila tillstånd som anges av den Loschmidska temperaturgradienten. Konvektion uppstår (på grund av gravitationen) när ett luftpakets temperatur avviker från sagda gradient och tenderar att återföra paketets temperatur till vad gradienten föreskriver.
Så jag har inget att invända mot din utsaga i punkt 2 att ”Det är konvektionen som upprätthåller den gravito-termala effekten”, för jag inser att ”upprätthåller” ska läsas som ”vidmakthåller” i enlighet med Maxwells förklaring till uppkomsten och vidmakthållandet av det han kallade en ”konvektiv termisk jämvikt”.
Men Johan (#87 punkt 2) har blivit förbryllad av din utsaga, vilken han tolkar som att du anser att det krävs konvektion för att det ska uppstå en gravito-termal effekt. Det är kanske rätt tolkat. Så än en gång, det krävs ingen konvektion för att det ska kunna uppstå en gravito-termal effekt, utan det räcker med luftmolekylernas egenrörelse.
# Montelius, Pettersson och Åsbrink.
Så som utgångsvärdet i simuleringen var är det en mycket stabil situation med varm luft (dvs samma temperatur) överst i volymen. Situationen är så stabil att det nog inte räcker med att lägga gravitation på alltsammans för att saker skall börja hända.
Som antyds i coombes-laue.pdf, länken i #48, kanske vi bör föra in luftpaket med olika temperatur för att övervinna den stabila situationen och kicka igång bildandet av en lapsrate. Man kan jämföra gravitationen med en centrifug. Det går inte att centrifugera en homogen gas eller vätska eftersom det inte finns något fysiskt som skiljer partiklarna åt.
Fri flyktväg för en molekyl är en tiotusendels mm. Det behövs inte stora
avrundningsfel för att dölja den kastkurvan. Det behövs 100 miljarder studsar för att nå från marken till tropopausen endimensionellt (utan vektor) och betydligt fler tredimensionellt.
#89 Gösta Pettersson
Jag håller med sig om att det är konstigt och jag har inte satt mig in i detaljerna i Loschmidts bevis men jag tror jag har förstått grundmeningen – och den vara jag som sagt helt övertygad om att den skulle gälla.
Betraktar man en partikel i ett system så gäller Loschmidts teorem trivialt. Det gäller även i ett system med flera partiklar – om dessa ligger exakt ovanför varandra dvs aldrig studsar i sidled (en 1D värld).
När vi har två partiklar i rörelse i ett 2D-rum så händer något. Vertikal rörelseenergi kan bli horisontell rörelseenergi som kan bli vertikal osv. Som in mitt experiment 2 där jag har två partiklar så återfinns titta som tätt en partikel ovanför det som ursprungliga maximala höjden. Vi har fått en fördelning av energin mellan partiklarna som gör att de kan bidra till temperaturen på högre höjder. Kan detta förklaras i Loschmidts teorem?
När vi kastar om flera partiklar så får krockarna energin att spridas mer och mer …. vilket i slutändan – i simuleringen – ger upphov till en uniform temperatur.
#83 Lars.
De förklarar det med att.
”Då luftpaketet som stiger puffar undan annan luft åtgår energi som tas från luften i det stigande och utvidgande luftpaketet, därvid avkyls det”
Stämmer väl med fysiken ?
# Montelius, Pettersson och Åsbrink
Kan denna länk kasta lite ljus över tillvaron?
Sofia D. Wechsler ställer en fråga som Janusz Pudykiewicz, Neal King, Lothar Fritsche och V. T. Toth försöker svara på;
https://www.researchgate.net/post/The_Loschmidt-Maxwell_polemic-thermodynamic_equilibrium_in_the_gravitational_field
#92 Johan Montelius
”När vi har två partiklar i rörelse i ett 2D-rum så händer något.”
Det är väl detta som Coombes och Laue visar i din gamla referens.
https://tallbloke.files.wordpress.com/2012/01/coombes-laue.pdf
Det är synd att ingen har kommenterat min tidigare kommentar:
”Enligt termodynamikens andra sats kommer vid jämvikt i ett slutet system, där energiinnehållet är konstant, molekylrörelser och temperaturer att ställa in sig så att det inte längre kan utföra något arbete. Detta kan endast uppnås om temperaturen är konstant i hela behållaren.”
Att gravitationen inte skulle ha en avgörande betydelse för hur temperaturen blir i atmosfären verkar vara en osannolik slutsats. Gravitationen verkar på allt som har en massa (varken det är partiklar, molekyler, atomer etc.). Det är gravitationen som ger oss en atmosfär och håller den massan på plats runt vår jord. Runt jorden finns gravitationskraft i atmosfären som minskar allteftersom man flyttar sig bort från jordens centrum. Atmosfären kan delas in i en massa undersfärer (olika avstånd till jordens centrum) där samma styrka/storlek råder på tyngdkraften.
På något sätt är gravitationen/tyngdkraften med hela tiden och påverkar var partiklar/molekyler/massa placerar sig över tid. Därmed även hur det ger temperaturskillnader i atmosfären när energiflöden förs in i sammanhanget.
#96 Munin
”Att gravitationen inte skulle ha en avgörande betydelse för hur temperaturen blir i atmosfären verkar vara en osannolik slutsats”
… och vem har dragit den slutsatsen?
Frågan är om gravitationen i sig ger upphov till en temperaturgradient.
Bjerke #95. Att ingen svarar kan bero på att det skrivna är så vagt. Ordet ”konstant” som finns med två gånger vad betyder det, att det är likformigt eller att det inte förändras? På samma sätt, vad betyder ´jämvikt’ och ”molekylrörelser och temperatur” är inte det samma sak – nästan?
Om du hittar någon bra lärobok som beskriver mer utförligt så ge mig en länk. Jag är lika nyfiken som du.
#92 Johan Montelius
”Jag håller med sig om att det är konstigt och jag har inte satt mig in i detaljerna i Loschmidts bevis men jag tror jag har förstått grundmeningen – och den vara jag som sagt helt övertygad om att den skulle gälla.”
Loschmidts bevis är inte mera komplicerat än så som jag sammanfattade det i #89 och jag är övertygad om att du har förstått grundmeningen. En avgörande förutsättning för uppkomsten av den Loscmidtska gradienten är att systemet är adiabatiskt med ett konstant energiinnehåll U. Storleken av U (och dess fördelning på kinetisk- resp. lägesenergi) i din partikelbox avgör du med dina val av initialvärden för partiklarnas antal, lägen och vektoriella hastigheter. Vad jag skulle vilja veta är om ditt utgångsvärde för U är bibehållet vid simuleringens slut.
Detta som ett första steg i ett försök att kolla vad som skulle kunna ha gått snett i dina simuleringar. Sen kan du ju också kolla vilken gravito-termal effekt du enligt Loschmidt borde förvänta dig se för dina valda initialvärden. Den kanske är så liten att den finns där men inte gör väsen av sig. Och boxens tak är för mig en styggelse som bör förläggas till en höjd dit ingen mänsklig fot eller partikel kan nå.
Ett för mig som empiriker väsentligt faktum är att det i realiteten finns en troposfärisk temperaturgradienten som låter sig väl beskrivas av Loschmidts ekvationer. Och som teoretiker är jag lika nyfiken som du på varför du inte får fram effekten i dina simuleringar, utan snarare får fram ett isotermiskt tilltånd som definitivt inte stämmer överens med vad som observerats. För jag tycker precis som du att effekten borde kunna påvisas i simuleringar. Även i 2D-miljö.
#99 Gösta Pettersson
”Vad jag skulle vilja veta är om ditt utgångsvärde för U är bibehållet vid simuleringens slut. ”
Yep, jag la in det rätt tidigt i simuleringen så att man skulle vara säker på att man inte förlorad (eller skapade) någon energi av misstag. I början på varje körning så sveper jag över alla partiklar och summerar deras kinetiska och lägesenergi. Det stämmer, allt finns med.
” Sen kan du ju också kolla vilken gravito-termal effekt du enligt Loschmidt borde förvänta dig se för dina valda initialvärden.”
Detta är vad jag borde göra men ge mig ett exempel. Jag har inte satt enheter i min simulering och det liknar inte partiklar i en atmosfär eftersom deras radie är 1 och höjden satt till 10.000 (rätt stora molekyler mao . Men som sagt Loschmidt utalar sig generellt om partiklar i ett gravitationsfält så vi borde se en gradient även i denna simulering.
. Men som sagt Loschmidt utalar sig generellt om partiklar i ett gravitationsfält så vi borde se en gradient även i denna simulering.
Om vi sätter taket till 20.000, bredden till 1000, radien till 1, massan till 1. Vad skall vi välja g som? Hur skall vi initialisera systemet? Jag har nu en version där man kan sprida ut partiklarna med slumpad hastighet och låta dem sprida sig uniformt i rummet, efter t.ex. 1000 tidsenheter så slår man på gravitationen för att se vad som händer. (och nu inser jag att man i samma veva vill höja taket om man vill undvika att några partiklar studsar så högt)
Ge mig ett värde på g, hur vi skall initialisera systemet och en förutsägelse enligt Loschmidt.
”Ett för mig som empiriker väsentligt faktum är att det i realiteten finns en troposfärisk temperaturgradienten som låter sig väl beskrivas av Loschmidts ekvationer.”
Håller med, men som jag visade i de mer add-hoc simuleringarna med varmt golv och iskallt tak så har gravitationen en stor inverkan på hur en existerande gradient ser ut. Det kanske är det som spökar, gravitationen är en faktor och det är den man får ut – men det betyder inte att den är orsaken.
Johan M #100. Bra ansats. Kanske borde du införa molekylerna inte en och en utan som en volym av gasen med olika temperatur. Det triggar turbulens i det simulerade rummet som kan vara viktig för att fånga upp gravitationen och bilda gradienten (jämför centrifug #91).
G.P. #99 ”Den kanske är så liten att den finns där men inte gör väsen av sig.”
Det var vad jag föreslog i #47. ”Ser man på diagrammen ”temperaturutveckling olika höjder” så finns det en intressant skillnad. Det är bara att ta fram förstoringsglaset och titta på kurvorna till höger.”
Välj en annan skala på Y-axeln så kanske vi ser det vi söker.
.
#101 Lars Cornell
Partiklarna i alla simuleringar ovan har släppts samtidigt från ca 1/4 av höjden med liten horisontell hastighet. Det kvittar hur du inför dem så länge som de börjar kollidera. Efter att tag har de hittat den utbredning och fördelning som de sedan håller,
#98 Lars Cornell
Kul att du tar dig tid att svara. Jag skrev följande:
”Enligt termodynamikens andra sats kommer vid jämvikt i ett slutet system, där energiinnehållet är konstant, molekylrörelser och temperaturer att ställa in sig så att det inte längre kan utföra något arbete. Detta kan endast uppnås om temperaturen är konstant i hela behållaren.”
Här är mina svar på dina frågor:
1. I ett adiabatisk kärl förändras inte dess totala energiinnehåll.
2. Att systemet är i jämvikt betyder att det ställt in sig i sitt sluttillstånd. Jämför t.ex. med Johans modell där det tar en tid innan alla redovisade parametrar har svängt in.
3. Jag håller med dig om att temperatur är nästan samma sak som molekylhastighet i modellen eller snarare proportionell mot molekylhastighet i kvadrat.
Termodynamikens andra lag kan uttryckas på många sätt. En enkel beskrivning är:
Om det finns möjlighet till värmeledning eller strålning kommer värme alltid att flöda från det varmare området till det kallare.
Det vore också hyggligt om Gösta Pettersson ville berätta varför hans teori inte strider mot termodynamikens andra huvudsats.
Det var en interessant artikel, over 100 kommentarer.
Jeg er stødt på begrebet af og til og det giver anledning til mange funderinger.
Luft der stiger og falder er et bevis på at noget sker, CO2 kan ikke afkøle/opvarme det så hurtigt via sin stråling.
Din simulering viser meget godt hvad jeg forestiller mig sker, hvis der ingen klimgasser var. Luften vil få samme temperatur overalt og al konvektion ville stoppe.
Lapserate på Venus er meget tæt på den teoretiske bestemt af gravitationen, og der er ellers CO2 nok.
Spørgsmålet er vel hvilken betydning CO2 har på det øverste luftlags temperatur, for derefter er det bestemt af lapse rate.
Johan M:
Jag har kört lite egna simuleringar på liknande sätt som du, och har landat i samma slutsats d.v.s. att en temperaturgradient inte uppstår endast p.g.a. gravitation.
Däremot är ju detta ett 100% teoretiskt scenario utan någon in- eller utflöde av energi. I verkligheten (specifikt jorden och dess atmosfär) sker ju alltid in- och utstrålning och inget system befinner sig i termodynamisk jämvikt.
Mina simuleringar tycks visa att gravitation plus ett visst in- och utflöde av energi (d.v.s. ett system som inte är i termodynamisk jämvikt) faktiskt uppvisar en temperaturgradient. Tar man bort gravitationen eller in- och utflödet av energi till/från systemet så blir gradienten mycket mindre eller försvinner helt.
Detta är såvitt jag kan förstå exakt samma slutsats som Claes Johnson presenterar i denna bloggpost (https://claesjohnson.blogspot.com/2013/01/new-lapse-rate-by-gravitation-loschmidt.html), se detta stycke:
”We thus find support of Loschmidt’s conjecture of still air solutions with the dry adiabatic lapse rate, in the absence of heat conduction. In the presence of (small) heat conduction, it appears that a (small) external source will be needed to maintain the lapse rate. Of course, in planetary atmospheres external heat forcing from insolation is present.”
(Värmeledning, ”heat conduction” finns ju med i både din och min simulering i och med att partiklar kan krocka med varandra och utbyta energi.)
Så min egen personliga tolkning är att Loschmidt rent tekniskt hade fel, men att detta är helt irrelevant för en ev. beskrivning av temperaturgradienten i jordatmosfären eller något annat i verkligheten existerande system.
#103 Bjerke. Att värme (energi) alltid flödar från det varmare området till det kallare är inte sannt. Du har skrivit så förr och nu upprepar du det felet.
https://eddler.se/lektioner/wiens-forskjutningslag-och-stefan-boltzmanns-lag/
#103 Lars-Eric Bjerke
”Det vore också hyggligt om Gösta Pettersson ville berätta varför hans teori inte strider mot termodynamikens andra huvudsats.”
Tack för försöket till smicker, men i min serie av KU-inlägg har jag har inte lagt fram några egna teorier utan försökt upplysa om hur det sena 1800-talets atmosfärsforskare (Maxwell, Loschmidt, Boltzmann m fl) lyfte fram gravitationen och den gravito-termala effekten som en synnerligen väsentlig faktor för förståelsen av de troposfäriska temperaturförhållandena. Att så är fallet informerades jag om när jag på 1960-talet gavs (elementär) meteorologisk undervisning där man som belägg för den troposfäriska temperaturgradientens gravitationella ursprung framhöll att gradientens lapse rate är proportionell mot gravitationskonstanten. Då var Maxwell-Loschmidts syn med rätta allmänt accepterad inom meteorologisk vetenskap.
Enligt min uppfattning var det inte förrän politiker under sent 1900-tal försökte ta befäl över hur de vetenskapliga resultaten ska tolkas som hypoteserna om växthuseffekter började bli populära och nyttjas för politisk skrämselpropaganda. Belyst av att den politiska organisationen IPCC (bestående av diplomatiska representanter för FN:s medlemstaters regeringar) i sin första rapport deklarerade att den 32-gradiga atmosfärseffekten är en växthuseffekt, trots att den ur vetenskaplig aspekt enligt Maxwellskolans argumentering uppenbart är en gravito-termal effekt.
Beträffande termodynamikens andra huvudsats (2nd law), så förmodar jag din undring föranleds av det sena 1800-talets kontrovers mellan Maxwell och Loschmidt rörande vilka temperaturförhållanden som upptår i en cylindriskt innesluten gas. Loschmidts förmodan att det på grund av gravitationen uppstår en temperaturgradient bestreds av Maxwell med hänsvisning till 2nd law som enligt hans mening borde ge upphov till ett isotermiskt jämviktstillstånd. Reminiscenser av denna kontrovers återfinns bland annat i Adeptens kommentar #84 och #94.
Min syn på det hela är att termodynamikens usprungliga huvudsatser baserades på förhållanden som gäller för skeenden i laboratoriemässig höjdskala där gravitationella effekter är av försumbar storlek. Loschmidt utsträckte skalan till höjder där gravitationen är av betydelse. Må vara att kontroversen rörande temperaturen i en cylindriskt innesluten gasmassa ännu inte är experimentellt helt tillförlitligt sliten. Men vad den oinneslutna atmosfären beträffar var Maxwell och Loschmidt helt eniga. Det finns en gravito-termal effekt som ger upphov till en troposfärisk temperaturgradient.
Att uppkomsten av denna temperaturgradient inte strider mot
någon termodynamisk huvudsats befästs av att den föreligger.
#104 Svend+Ferdinandsen
”Spørgsmålet er vel hvilken betydning CO2 har på det øverste luftlags temperatur, for derefter er det bestemt af lapse rate.”
…och inte bara CO2, vattenånga finns det gott om i troposfären.
#105 KM
Härligt att du kommit fram till liknande resultat
”..utan någon in- eller utflöde av energi”
Ja, helt riktigt och det var med avsikt. Teorin om den gravito-termala effekten säger att gravitationen i sig skulle ge upphov till en temperaturgradient och det var det jag vill pröva. Det är ett 100% teoretiskt scenario eftersom vi vill fokusera på exakt en sak.
” … gravitation plus ett visst in- och utflöde av energi ”
Det är också min observation men orsaken till att vi då överhuvudtaget har en laps-rate är värme/kyla – gravitationen påverkar dess utseende.
”.. exakt samma slutsats som Claes Johnson presenterar ”
Tack, kom ihåg att jag läst hans resonemang men hade glömt bort det – och viktigt att du pekar på detaljen om konduktivitet. I den första simuleringen som jag gör, med bara en partikel, så har vi ingen ”konduktivitet” (om man nu kan tala om det med en partikel) och vi får som ett brev på posten en lapsrate. Jag säger också att vi skulle få samma resultat med flera partiklar – om de inte kolliderar. Redan när vi inför två partiklar som får kollidera händer något – vi har fortfarande en lapsrate men värmen sprider sig uppåt. Ju större konduktivitet desto mindre lapsrate (om vi inte inför värme/kyla).
”Så min egen personliga tolkning är att Loschmidt rent tekniskt hade fel, men att detta är helt irrelevant för en ev. beskrivning av temperaturgradienten i jordatmosfären eller något annat i verkligheten existerande system.”
Hmm, att han hade fel är vi överens om men har inte det en väldigt stor betydelse? Använder man Loschmidts resonemang så härleder man t.ex. att utav den lapsrate på 8C/km som vi har i troposfären så står gravitationen för huvuddelen och växthusgaserna för en mindre del. Separerar man dessa två komponenter i tron att de är oberoende av varandra så kommer man dra felaktiga slutsatser, eller?
#107 Gösta Pettersson
”.. temperaturgradientens gravitationella ursprung framhöll att gradientens lapse rate är proportionell mot gravitationskonstanten.”
Men detta är inte samma sak som att gravitationen i sig ger upphov till en gradient.
Vad säger Loschmidt om ett adiabatiskt system med två partiklar som släpps från halva höjden och vi har en gravitation.
I simuleringen, och jag vill hävda i verkligheten, så får vi ett resultat om de kolliderar med varandra och ett resultat om de åker de rätt igenom varandra. Loschmidt måste ha tagit hänsyn till detta och beskrivit temperaturgradient som beroende på tätheten i gasen.
J.M. #108 Lennart Bengtsson skrev 2023-10-12
Det inses lätt att mängden koldioxid uppgår till drygt 6 kg / m2 jordyta medan vattenångan i genomsnitt uppgår till 25 kg/m2 jordyta. På våra breddgrader och vintertid torde mängden CO2 och H20 i atmosfären vara desamma.
#111 Lars Cornell
Skillnaden är dock att CO2 är ,er eller mindre uniformt förekommande i atmosfären oberoende av höjd och temperatur. För vattenånga så är situationen en helt annan; mängden varierar betydligt med temperatur och höjd (upp till ca 20km).
#109 Johan M:
”Hmm, att han hade fel är vi överens om men har inte det en väldigt stor betydelse?”
Kanske men inte säkert, se längre ned…
”Använder man Loschmidts resonemang så härleder man t.ex. att utav den lapsrate på 8C/km som vi har i troposfären så står gravitationen för huvuddelen och växthusgaserna för en mindre del. Separerar man dessa två komponenter i tron att de är oberoende av varandra så kommer man dra felaktiga slutsatser, eller?”
Det beror nog på om man endast ser två möjliga slutsatser:
1. Loschmidts teori om den gravitotermala effekten är 100% korrekt, eller
2. Teorin om växthuseffekten är 100% korrekt och vi står därför inför en nära förestående klimatkris.
Jag tänker att det nog finns åtminstone ett tredje alternativ.
Först en par kontrollfrågor som jag funderat en del på: Växthusgasernas (främst H₂O och CO₂) specifika radiativa egenskaper ingår väl inte alls i de simuleringar som vi gjort? Alla gaser, även ”icke-växthusgaser” avger väl värmestrålning i någon mån enligt en approximativ svartkroppsstrålning?
Beroende på dina svar på ovanstående två frågor så kan den fortsatta diskussionen ta lite olika vändningar.
#106 Lars Cornell
Jag skrev att en enkel beskrivning av termodynamikens andra huvudsats är:
Om det finns möjlighet till värmeledning eller strålning kommer värme alltid att flöda från det varmare området till det kallare. Man kan förstås uttrycka detta mer stringent med hjälp av entropibegreppet. Dock förstår jag inte på vilket sätt din referens motsäger detta. Förklara gärna.
#113 KM
Rätt – partiklarna i min simulering har endast egenskapen: massa, storlek och en vektor för dess hastighet. Alla partiklar är identiska vad avser massa och storlek. Det enda sättet de interagerar är genom elastiska kollisioner (enbart konduktion ingen strålning). Partiklarnas kinetiska energi är helt och hållet deras hastighet (i kvadrat/2) inte någon intern vibration el.dyl.
”Alla gaser, även ”icke-växthusgaser” avger väl värmestrålning i någon mån enligt en approximativ svartkroppsstrålning?”
Nu är jag inte någon fysiker men jag skulle säga ja – men … inte i nogon form som liknar svartkroppstrålning. Varje atom eller molekyl kan avge strålning men i specifika band. En syrgasmoleky har inte så många frihetsgrader och kan därmed vare sig ta upp eller stråla ut en foton så bra. En gas har ju som ett fingeravtryck specifika band som de kan agera inom. Syrgas och kvävgas har små band jämfört med vattenånga eller koldioxid.
Så in en simulering skulle man nog sätt deras påverkan till 0 i jämförelse med de sk. växthusgaserna.
”Det beror nog på om man endast ser två möjliga slutsatser: …. det nog finns åtminstone ett tredje alternativ.”
Det ser jag definitivt. Jag tror dock att Loschmidt hade fel – eller i alla fall de som tolkar det som om gravitationen i sig ger upphov till en varmare atmosfär närmare ytan av en planet.
Att han inte har rätt innebär inte att vi har en klimatkris. Den kan vi skriva av på grund av andra anledningar (bla. den sk. bombkurvan som Gösta pekat på).
#115 Johan M:
OK, jag noterar ditt svar att icke-växthusgaser inte avger svartkroppsstrålning och dessutom strålar de väldigt lite jämfört med växthusgaser.
Men varför avger då solen (ett gasklot!) en i det närmaste perfekt svartkroppsstrålning på 5800 K? Solen innehåller ju mig veterligen inga större mängder växthusgaser?
https://physics.stackexchange.com/questions/467613/why-is-the-sun-approximated-as-a-black-body-at-5800-k
https://www.pas.rochester.edu/~blackman/ast104/composition.html
”The Sun is clearly mostly hydrogen and helium, with only a trace of heavier elements.”
Känns som att något inte stämmer här, har jag missat något?
#116 KM
Ta allt jag säger om dessa saker med en nypa salt men solen är ett plasmaklot och plasma i tillräcklig mängd och densitet kan avge strålning i de flesta frekvensbanden och blir då mycket likt en svartkropp.
En molekyl som O2 kan dels ta o upp och absorbera fotoner genom att en elektron i en av atomernas skal hoppar upp/ner en nivå. De fotonerna är dock mycket energirika, UV. Den kan även ta upp en infraröd foton och rotera mera. Dock så är den pga sin symmetri, inte bra på att ta upp en foton och öka sin vibration. När man räknar på växthuseffekten så är det framför allt i det infraröda spektrat man tittar eftersom det är i det spektrat som jorden stråla ut.
#117 Johan M:
OK, jag får nog läsa på lite mer om de radiativa skillnaderna mellan plasma och gas här känner jag.
”Jag tror dock att Loschmidt hade fel – eller i alla fall de som tolkar det som om gravitationen i sig ger upphov till en varmare atmosfär närmare ytan av en planet.”
Jo… Men givet kontinuerlig in- och utstrålning av energi (vilket som sagt alltid är fallet i ett någorlunda realistiskt scenario) så är ju lapsraten större för en planet med starkare gravitationsfält. Så det tycks helt klart finnas en gravitotermal komponent som kan härledas teoretiskt vilket också framgår av CJ:s redogörelse som jag länkade till här ovan.
Men hur som helst, jag tror vi är överens i stort – gott så!
#115 Johan Montelius
”massa, storlek och en vektor för dess hastighet”.
Med hur många decimaler lagras vinkeln? På en tiotusendels mm lång kastparabel blir vinklarna mycket små. Men de får inte försvinna för då blir det fel.
Bjerke #114. Tag en ficklampa, tänd den och rikta den mot solen. Vips så överför du energi från den relativt kalla ficklampan till den mycket varmare solen.
(Jämför #117 ”solen mycket likt en svartkropp”).
#118 KM
Vi är nog överens om det mesta även om att gravitationen påverkar lapsrate – men, det är inte den gravito termala effekten. Den gravito termala effekten säger att en atmosfär kommer ha en temperaturgradient enbart beroende av gravitationen. I praktiken säger den att en platt jord med en atmosfär bestående av 100% Argon som endast värms upp genom konduktion med markytan kommer att ha en temperaturgradient.
När man ser att jordens atmosfär har en gradient så säger man att man först skall räkna bort den gravito termala effekten och det som sen återstår (om något) är vad växthusgasernabidrar med.
plasma o gaser – det är ju till och med så att man i spectrat från solen ser en del svarta streck och det är spektrallinjerna för de olika grundämnena. Att solen i grunden strålar som en svartkropp har jag ingen aning om, säkert något med kvantfysik att göra
#119 Lars Cornell
Jag har vektorn representerad i dess två komponenter x-led, y-led. Det blir lite enklare att räkna på. Varje värde representeras med ca 15 decimaler plus exponent (Java double).
# 118 KM
Detta är en mycket avgörande slutsats för att få med vilka faktorer som bestämmer hur jordens klimatet är och vad som kan göra att det ändrar sig över tid.
Så fort in- och utstrålning förs in uppträder en gravito-termal effekt!
Det leder direkt till att det i varje förklaringsmodell av klimatet måste införas en beräkning av hur mycket som avgörs av denna faktor relativt andra faktorer.
Särskilt intressant blir att få vetenskapliga förklaringar till hur gravitation och energiflöden är i symbios/interagerarmed varandra.
Handlar det om att förklaringen måste sökas ner på atomernas nivå och hur de är uppbyggda och hur deras minsta delar fungerar vid inverkan från jordens gravitation när de befinner sig i atmosfären.
#123 Munin
”Så fort in- och utstrålning förs in uppträder en gravito-termal effekt!”
Nej, den gravito-termala effekten uppträder när vi har gravitation – den har ingenting med in och utstrålning att göra.
# 107 Gösta Pettersson
”Min syn på det hela är att termodynamikens ursprungliga huvudsatser baserades på förhållanden som gäller för skeenden i laboratoriemässig höjdskala där gravitationella effekter är av försumbar storlek.”
Dagens formulering av huvudsatserna med hjälp av begreppet entropi ger enligt min mening samma resultat för det aktuella teoretiska adiabatiska problemet vare sig man använder laboratorie- eller global skala. Johans modell med och utan gravitation är ett starkt indicium för detta, förutom andra huvudsatsen.
Jag håller med dig om att gravitationen har en mycket stor betydelse för temperaturens avtagande med höjden i den verkliga atmosfären (lapse rate) men det motsäger ju inte att vi får en högre temperatur på jorden av många andra fenomen som tillför eller flyttar om energi i atmosfären så att en laps rate linje parallellförskjuts eller bucklas till. Om man tänker på det motsatta extremfallet till det adiabatiska d.v.s. har en extremt stor omblandning i atmosfären går ju också laps raten mot noll.
#120 Lars Cornell
”Tag en ficklampa, tänd den och rikta den mot solen. Vips så överför du energi från den relativt kalla ficklampan till den mycket varmare solen.”
Visst. Jag trodde det var självklart att alla kroppar avger strålning. Det är naturligtvis nettoflödet av värme termodynamikens andra huvudsats menar när den säger att värme alltid går från ett varmt område till ett kallare.
Vad jag kan förstå är det som skiljer lådorna med eller utan gravitation är att trycket i lådan med gravitation är högre ju närmare botten man kommer. Dvs fler partiklar längst ner än högst upp.
Kan det ha betydelse för hur en temperaturgradient kan skapas när värme tillförs och tappas av i systemet?
#120 Lars Cornell & #114 Bjerke
Tag en ficklampa, tänd den och rikta den mot solen. Vips så överför du energi från den relativt kalla ficklampan till den mycket varmare solen.
Javisst! Men värme överförs inte. Det är solen som värmer ficklampan. Värmeöverföring är nettoflödet av energi. (Klarblå partikelfri himmel med solen i zenith. Finns moln eller om solen står lågt i ”vanlig” molnfri atmosfär blir det atmosfären som värms av båda.)
Två svartkropsstrålare, typ värmeplattor, som har samma temperatur och hålls nära varandra strålar båda i enlighet med Stefan-Boltzmanns lag. Strålningen, Energiflödet blir dock lika i båda riktningarna så nettoflödet blir noll. Dvs ingen värme överförs.
Engelska Wikipedia har en korrekt beskrivning av Stefan-Boltzmanns lag: https://en.wikipedia.org/wiki/Stefan%E2%80%93Boltzmann_law Strålningen är oberoende av omgivningen.
Svenska Wikipedia https://sv.wikipedia.org/wiki/Stefan%E2%80%93Boltzmanns_lag presenterar en ur Stefan-Boltzmanns lag härledd formel för värmeöverföringen från en kropp med temperaturen T till en omgivning med temperaturen T0 och påstår att denna härledda formel är Stefan-Boltzmanns lag.
Som läget är just nu finns alltså två helt olika formler som påstås vara Stefan-Boltzmanns lag. Naturligtvis är båda formlerna korrekta, men det kan inte vara rätt att ge dessa olika formler samma namn.
Formuleringen i svenska Wikipedia har lett till en hel del förvirring för den har ibland tolkats som att den utstrålade energin från en varm yta skulle bero av omgivningen – dvs att versionen i engelska Wikipedia skulle vara fel. Det är den naturligtvis inte! Båda formlerna är korrekta, den ena handlar om utstrålad effekt, den andra om värmeöverföring genom strålning.
#10 Magnus Cederlof
Du skriver: ”Den temperatur-gradient vi observerar i verkligheten beror alltså på att konvektionen (värmeledning genom luftrörelser) är snabbare än värmeledningen (kollisioner). Men om jorden varken skulle ha växthusgaser eller tillförd energi från solen, skulle atmosfären ha samma temperatur på alla höjder.”
Detta tror jag är den korrekta förklaringen. Dock lite utvidgad: Konvektionen är snabbare än alla de andra mekanismerna för värmeöverföring. Värmeledning, strålning och vattnets fasomvandlingar.
För övrigt gäller inte laps rate alltid. Det kan bli inversioner. https://www.smhi.se/kunskapsbanken/inversion-1.28269 De kan bli omfattande och täcka hela Nordeuropa eller Stilla Havet från Hawaii till Kalifornien. Radioamatörer tycker det är väldigt kul därför att inversionsskiktet fungerar som en spegel och gör att kortvågiga signaler utbreder sig tvådimensionellt och följer jordytan med mycket låg dämpning. Kall fuktig luft med dimma nära marken och varm torr luft ovanför. För radiovågor blir det totalreflexion mot tunnare medium.
# 124 Johan Montelius
Ja, det är lämpligare att använda gravitotermal komponent, som i inlägg # 118.
Det viktiga är dock den skillnad som visar sig när in- och utstrålning förs in i sammanhanget och att den skillnaden på något sätt har samband med gravitation. Då väcks intresset för hur det kan förklaras hur skillnaden uppkommer och om det har en giltighet även i den verkliga atmosfären.
#14 Lars-Eric Bjerke
Detta kan synas teoretiskt: ”Enligt termodynamikens andra sats kommer vid jämvikt i ett slutet system, där energiinnehållet är konstant, molekylrörelser och temperaturer att ställa in sig så att det inte längre kan utföra något arbete. Detta kan endast uppnås om temperaturen är konstant i hela behållaren.
Tänk ett termoelement av två olika supraledare. En ”lödpunkt” vid marken, den andra i på en höjd av 1 km. Temperaturskillnaden på cirka 6 grader kommer att driva en ström som kan användas till nyttigt arbete. Varifrån kommer energin? Gör vi om experimentet i en perfekt isolerad vertikal cylinder kommer det så småningom nödvändigtvis att bli samma temperatur i toppen som vid botten. Annars skulle vi ha en perpetuum mobile. Det ligger nära till hands att gissa att temperaturen skulle bli densamma i hela cylindern även utan termoelementet.
Den gravito-termala effekten kräver ett energiflöde som möjliggör energiutvinning med ideala termoelement. Hur det fungerar i detalj vet jag inte, men uppenbart är det något som saknas i simuleringarna.
Kanske ett laps rate skulle uppstå ifall värme tillförs underifrån och alla partiklar tillsammans förlorar samma energimängd. Det borde inte spela någon roll hur det sker i detalj. T.ex. kan alla partiklar förlora samma mängd energi per tidsenhet förutom de vars energi inte räcker. Överskottet som uppstår får fördelas på övriga partiklar. Jag kan också tänka mig att slumpvis var tionde partikel står för hela energiförlusten ”genom strålning.” Taket borde kunna vara en perfekt spegel eller vara så högt upp att inga partiklar når det. Borde vara ekvivalent. En partikel som nått väldigt högt har extremt låg sannolikhet att kollidera med någon annan partikel så den kommer att återvända nedåt med oförändrad energi så småningom som om den hade träffat en ”spegel”
#130 Munin
”Det viktiga är dock den skillnad som visar sig när in- och utstrålning förs in i sammanhanget och att den skillnaden på något sätt har samband med gravitation.”
Utan gravitation så hade vi inte haft någon atmosfär. Vi har den gravitation som vi har och – detta är frågan – en atmosfär utan växthusgaser kommer vara isoterm (modulo konvektion som kommer av dag/natt, breddgrad mm).
När man inför växthusgaser så kommer dessa att skapa en skillnad i temperatur från höga höjder där de verkar avkylande till lägre höjder där de verkar uppvärmande. Den gradienten som vi får är beroende på den mängd partiklar vi har på de olika höjderna – och det är självklart ett resultat av gravitationen. Den tryckskillnad som gravitationen skapar är inte vad som menas med gravitotermal effekt,.
#127 thun
”Kan det ha betydelse för hur en temperaturgradient kan skapas när värme tillförs och tappas av i systemet?”
Låt oss göra ett tanke experiment. Vi har en låda 1000×1000 med partiklar uniformt utspridda och ingen gravitation. Temperaturen är isoterm i hela lådan.
Låt oss ha en magisk låda där dess övre sida är direkt kopplad till dess botten dvs ett A4-papper som vi tejpar ihop till en cylinder.
Vid jämna mellanrum så kommer varje partikel att minska i hastighet (om den har någon) och skjuta ut två fotoner – en uppåt och en nedåt. Dessa fotoner slår in i någon annan partikel som då ökar i hastighet.
Vår låda kommer fortfarande vara isoterm.
ta nu bort tejpbiten så att vi har ett plant A4-papper. De fotoner som slår i dess övre kant förvinner ut i världsrymden, de som slår i golvet reflekteras uppåt.
Kommer vi ha en temperaturskillnad mellan de olika lagren?
# 118 KM
”The continuous (as distinct from the line) spectrum of the Sun is produced primarily by the photodissociation of negatively charged hydrogen ions (H−)—i.e., atoms of hydrogen to which an extra electron is loosely attached. In the Sun’s atmosphere, when H− is subsequently destroyed by photodissociation, it can absorb energy at any of a whole range of wavelengths and thus produce a continuous range of absorption of radiation. The main source of light absorption in the hotter stars is the photoionization of hydrogen atoms, both from ground level and from higher levels.”
Så var det med den saken
#131 Leif Åsbrink
Du frågar varifrån energi kommer för att skapa en temperaturdifferens till ett termoelement.
Svar:
– I fallet med en verklig atmosfär kommer energin från solen via atmosfären som får sin temperaturdifferens genom alla fenomen som uppträder där.
– I fallet med en adiabatisk vertikal cylinder, som har varit ifred ett tag, finns ingen temperaturdifferans och således fås inget arbete via termoelementen.
– Jag kan inte se något fel i Johans simuleringar.
Det vi kallar temperatur är den kinetiska energin i gasen.
I ett ”öppet” rum i ett gravitationsfält måste en gas (mångpartikelsystem) föredelas så att kinteisk energi + potentiell energi har ett specifikt förhållande, d.v.s. totala energiinnehållet (2*T+P = konstant).
I en sluten låda kommer partiklarna föredela sig så att de med högst kinetisk energi har större sannolikhet att befinna sig vid taket än partiklar med låg kinetisk energi.
Detta gäller om skillnaden i potentiell energi mellan golv och tak är liten i förhållande till partiklarnas genomsnittliga kinetiska energi.
I en sluten låda blir det varmare vid taket (vilket även märks hemma).
I ett ”öppet” rum kommer temperaturen att sjunka med höjden (p.g.a. gravitationen).
Skulle tycka det var intressant med en simulering med lågenergetiska partiklar, d.v.s. att den potentiella energin är en signifikant del av partikelns energi.
#123, #130 Munin:
Ja, det känns som det finns något att gräva vidare i här även om hela teorin med rätt terminologi kanske inte riktigt är på plats ännu (för mig åtminstone).
#121, #134 Johan M:
OK, jag förstår hur du tänker och tack för info om vätejonernas betydelse för det kontinuerliga solspektrat.
Men…
En till sak som jag testade i min simulering var att låta marken värmas av solen under ”dagen” och kylas mot rymden under ”natten”. Då upprätthölls temperaturgradienten både dag och natt utan att gasmolekylerna själva hade förmågan att avge sin energi radiativt.
Så jag funderar på om det kan vara så enkelt att just det faktum att systemet aldrig tillåts närma sig en termodynamisk jämvikt kan vara den egentliga orsaken till temperaturgradienten – återigen i kombination med gravitationen?
Om den hypotesen stämmer så spelar ju atmosfärens sammansättning med eller utan växthusgaser ingen större roll i sammanhanget.
Skulle vara intressant om du hade möjlighet att testa själv och se vad du får fram i ditt program för motsvarande scenario.
#135 Lars-Eric Bjerke
Det är klart att det måste vara solen, men hur går det till? Dvs varför blir det en temperaturgradient?
Se min kommentar #85, tankeexperiment a)
#90 Gösta Pettersson hävdar ”Det grundläggande gravito-termala sambandet U = cp T + g m h gäller även i sådana fall” Jag ville med min fråga peka på att det inte räcker med en varm yta under en atmosfär på en stillastående atmosfär. På grund av symmetrin kan det inte bli någon horisontell strömning i gasen och någon kylning av gasen genom strålning kan inte förekomma. Jag tror inte kvävgas formar dimerer vid aktuella tryck och temperaturer och i tankeexperimentens värld får vi försumma eventuell IR-strålning från sådana.
Jag menar således att Göstas argument är fel. Termoelementet i tankeexperimentet a) kan inte stadigvarande ge energi. i tankeexperimentet a) får atmosfären samma temperatur som ytan på grund av värmeledning.
Det stämmer utmärkt med Johans simuleringar vad jag förstår.
#87 Johan Montelius Kanske det kanske, men nu är inte fråga hur vi kan skapa en gradient utan varför det inte finns en gradient i en värld med bara gravitation och ingen värmekälla. Med hänvisning till ovanstående tycker jag man bör ställa frågan Varför skulle det finnas en gradient i en värld med gravitation och värmekälla om atmosfären saknar konvektion och strålning? Sambandet U = cp T + g m h räcker inte tycker jag mig ha visat.
Jag citerar Gösta Petterssons har inlägg ”Den gravito-termala effekten” Därför kom Maxwell omsider fram till att troposfären temperaturmässigt strävar mot vad han kallade en ’konvektiv termisk jämvikt’, med ett jämviktsläge bestämt av den gravito-termala effekten så som den uttrycks av torr- och våtadiabaterna.
Min slutsats: Utan konvektion ingen ”konvektiv termisk jämvikt” – då blir det i stället konstant temperatur. Nog skulle det vara kul att veta om konvektion på grund av både värme och kyla från bottnens olika sidor skulle ge en gravito-termal effekt i simuleringarna.
#122 Montelius
Flytande decimalpunkt och 15 decimaler låter betryggande.
#126 Bjerke. Javisst. Det är skillnaden mellan ’flödet’ (i plural) och ’nettoflödet’ som är poängen.
#128 Åsbrink. Ordet ’värme’ är ett förrädiskt ord eftersom det tydligen kan betyda olika saker för olika personer och i olika situationer. Jag undviker ordet annat än i vardagsspråk. För mig överförs ’värme’ i båda riktningarna, ficklampa sol, eftersom för mig ordet ’värme’ är detsamma som ordet ’energi’.
Om gumman Rut har en hink med varmt vatten när hon går till ladugården och möter sin gubbe Knut som har en hink med kallare vatten när har går i motsatt riktning då har bevisligen ”värme” överförts i båda riktningarna.
Jag sökte på ordet ”värme” och fann följande under rubriken ’definitioner’,
https://sv.wikipedia.org/wiki/
• Allt spontant energiflöde från ett system till ett annat orsakat av en temperaturdifferens mellan systemen kallas värme.[4]
Hoppsan, nu var det plötsligt inte energin som kallas ’värme’ utan flödet av energi.
Eftersom temperaturdifferensen inte förorsakar strålning kan det som överförs inte kallas ’värme’.
Men ”Ur ett termodynamiskt hänseende kan värme aldrig lagras i ett system.”
Sammanfattningsvis är definitionen av ordet ’värme’ förvirrande och ibland även motsägelsefull. Därför bör ordet undvikas i tekniska och vetenskapliga diskussioner.
#131 Åsbrink.
Jag tror att Biltema säljer en sådan anordning. Den levererar ’energi’ och förbrukar ’värme’.
https://www.fruugo.se/vedbrannare-varmedriven-flakt-eldstad-flakt-vedeldad-spis-vedspis-flakt/p-204393988-434477791
”Denna spisfläkt drivs genom att omvandla värme till energi utan att använda batteri eller el.”
#138 KM
”En till sak som jag testade i min simulering var att låta marken värmas av solen under ”dagen” och kylas mot rymden under ”natten”. ”
Tagen, det låter som en intressant idé.
#139 Leif Åsbrink
Ja det behövs både en värmande del och en avkylande del för att skapa en temperaturskillnad. Jag kör nu lite försök med dag/natt som kanske skapar en temperatur gradient. Skall även prova med en kall och en varm sida av golvet (vilket säkert skapar konvektion och kanske även en gradient)
#136 JonasW
”I en sluten låda kommer partiklarna fördela sig så att de med högst kinetisk energi har större sannolikhet att befinna sig vid taket än partiklar med låg kinetisk energi.”
Ja det är ju en rimlig slutsats …. som visar sig vara fel när man försöker simulera systemet. Det är sant så länge du har så få partiklar så att de inte krockar. Har du tillräcklig täthet så kommer temperaturen att jämna ut sig.
Hej
Väldigt intressant, och ÖPPEN debatt.
Lite svårt att förstå och smälta i alla lägen för en högskoleingenjör men stort tack!
”Är det människans utsläpp av koldioxid som styr klimatet?”
* Om man ska tro ”Maxwell” så torde svaret bli NEJ!
* Har växthusgaser större betydelse så kommer alla osäkerheter och antaganden som IPCC gör i spel. Har man ett öppet sinne torde väl AGW-CO2 stå för någon tiondels grad eller två? Fördelarna torde överväga nackdelarna av denna energikälla? Alternativen framstår inte som särskilt önskvärda.
OT; Hur kan man tro att människans utsläpp av koldioxid ska, efter år 1750, plötsligt ersätta de faktorer som under miljoner år skapat väder och klimat? (I synnerhet om man inte har klart för sig vilka och vad dessa ”historiska faktorer” är!)
Med vänlig hälsning, Mats, Växjö
Hej Johan,
vilket intressant numeriskt experiment du gjort.
Jag skulle också ha trott att det skulle uppstå en temperatur-gradient och som jag antydde i en tidigare kommentar så tror jag att ditt experiment i princip handlar om värmeledning, medan det varkar svårt att få in ”strömning av luftpaket” i ditt experimentl
Jag konstaterar av kommentarerna att döma att jag inte var den ende som blev förvånad. Meu du ska hursomhelst ha beröm för ditt simuleringsexperiment.
#144 Mats Växjö
Enligt simuleringen spelar tyngdkraften ingen roll för lapse rate för de som tror på teorin om gravitationsförstärkning (gravito-termala effekten) som hävdar att planetens yttemperatur bara är en funktion av absorberat solljus och atmosfärstryck.
Och den förklarar inte heller varför det förmodas att temperaturen ökar med ca 0,13 grader per decennium
Förövrigt tycker jag som du att ”debatten” är intressant och givande. Önskar därför att fler kunniga kommer med i debatten som gärna kan fortsätta med ytterligare 100-tals kommentarer
Jag tycker att någonting saknas här, för verkan av gravitationens tryck ökar inte bara vertikalt nedåt, utan också horisontellt, eller med andra ord, minskande omkrets. Det vertikala trycket är så mycket större nära jordytan jämfört med den långt ut. Atmosfärens volym ökar med ökande omkrets, vilket innebär att molekylernas rörelseutrymme närmre jordplanet är mindre än det längre ut. Vid uppvärmning av luften är det därför naturligt med en expanderande rörelse utåt. Men eftersom den atmosfäriska volymen ökar utåt, så minskar också friktionen mellan molekylerna och därmed svalnar den expanderande luften.
Lars-Erik Bjerke
Om man tänker på det motsatta extremfallet till det adiabatiska d.v.s. har en extremt stor omblandning i atmosfären går ju också laps raten mot noll.
Nej, det er blandt andet omblandingen der giver lapse rate. Stigende og faldende luftmasser.
Med strålingsaktive gasser i luften vil der også være en lapse rate. Fra jordoverfladens 400W/m2 til de øverste luftlag med 140W/m2 korrigeret for gassernes evne til stråling.
Hvordan fordelingen så er mellem stråling og gravitation i denne lapse rate er jeg ikke sikker på, men hælder en del mod gravitationen.
#147 Björn
I simuleringen så har vi en ruta på 1.000×10.000 enheter och låt oss kalla det meter. Hur stor skulle skillnaden vara mellan golv och tak om vi skulle simulera jordens krökning?
Jordens radie är 6371 km vid jordytan och har då en om krets på 2*pi*6371. Tio kilometer upp är den 2*pi*6381 dvs 6381/6371 gånger längre. I vår simulering skulle då längden vid ”taket” vara 1001.5 m . Skillnaden är så lite att man nog kan säga att det inte är där skon klämmer.
#145 Sten Kaijser
”..medan det varkar svårt att få in ”strömning av luftpaket” ”
Ja, men det är inte för att det är svårt utan för att det inte förekommer om vi inte inför kalla och varma sektorer. I den första serien av simuleringar så är systemet aiabatiskt och det finns ingen anledning till att vi skulle se större paket röra sig i modellen. Det är som du säger en simulering av konduktivitet – och den gravito-termala effekten ska visa sig där, den är inte beroende av konvektion.
Jag har gjort simuleringar där ena sidan av golvet är varmt och andra kallt och visst får man en luftcirkulation som ett brev på posten. Vill man simulera detta bättre så bygger man nog dock en annan typ av simulator där man just talar om regioner i atmosfären och hur dessa gör utbyten med grannar.
Johan Montelius #150
Gravitationen og et koldt tag og varmt gulv giver en gradient, men hvad er årsag og virkning.
Kan du simulere uden tag og uendelig højde? Det kunne være en anden model af virkeligheden, hvor du ikke behøver at lægge et koldt tag på.
Jeg er vildt forvirret af dine resultater.
Trykfordeling
Uden varmetransport får du næsten ens temperatur ved alle højder. Alligevel har du flere partikler i bunden end i toppen, altså større tryk i bunden.
Da partiklerne startede midtvejs må en del være faldet ned og nogle faldet op. Det burde give højere temperatur i bunden end i toppen.
Du forklarer det med sammenstød, men jeg kan ikke følge dig her.
#151 Svend Ferdinandsen
”….men hvad er årsag og virkning.”
Exakt det som vi vill ta reda på och vad är inte enklare än att man gör två experiment 1/ där man inte har något kallt tak eller varmt golv och 2/ där man inte har någon gravitation.
I det första fallet ser vi att vi inte någon temperaturskillnad så gravitationen kan inte vara en orsak i sig, eller hur?
I det andra fallet ser vi hur gradienten mer och mer liknar ett vertikalt streck när vi sänker värdet på gravitationen. Skulle vi sätta gravitationen till noll så skulle efter ett tag alla partiklar befinna sig i ett fryst tillstånd under taket.
Ergo – orsaken till att vi har en gradient är inte gravitationen utan det kalla taket och varma golvet. Gradientens utseende påverkas av gravitationen.
”Kan du simulere uden tag og uendelig højde?”
Ja, inga problem – men hur skulle det förändra saker? I den simulering som jag visar så är i genomsnitt 4 partiklar av 10.000 i det översta lagret. Vad skulle förändra saker om dessa fick sprida sig ännu högre?
”Du forklarer det med sammenstød, men jeg kan ikke følge dig her.”
Gör ett tankeexperiment med två partiklar som släpps, från vila, från en höjd X; fullständigt elastiska kollisioner och en gravitation. Kommer någon av partiklarna någonsin studsa högre än höjden X?
Johan M:
Ursäkta på förhand för tjatandet!
Men jag lyckas – som jag kanske redan antytt – att i en sådan här simulering med fullständigt elastiska kollisioner få till en temperaturgradient endast med gravitation och ett konstanttempererat golv. Ett kallt tak behövs inte.
Detsamma gäller också med ett golv vars temperatur varierar upp och ned enligt en sinusvåg för att simulera uppvärmning dagtid och nedkylning nattetid – givet att ”rätt” dygnslängd och temperatursvängningsamplitud väljs.
Detta i ett system där partiklarna i sig inte har någon förmåga att vare sig absorbera eller emittera värmestrålning / IR.
Vilket alltså motsvarar ett scenario där atmosfären helt saknar växthusgaser och allt strålningsutbyte sker vid markytan.
Jag tänker att detta kan ha någon signifikans även om det inte är samma experiment som Loschmidts som ju rör vad som händer vid termodynamisk jämvikt dvs. ingen uppvärmning eller avkylning.
Villkoret termodynamisk jämvikt anser jag vara felspecificerat – redan av Loschmidt/Maxwell – vilket riskerar att leda oss till felaktiga slutsatser.
(För att förtydliga, om golvet ej värmer/kyler partiklarna så uppstår det ingen varaktig temperaturgradient eftersom att systemet då så småningom uppnår termodynamisk jämvikt.)
#154 KM
jag har gjort lite simuleringar – och lyckas inte
” … en temperaturgradient endast med gravitation och ett konstanttempererat golv.”
Det får jag också – men då har vi också en temperatur som stiger sakta, sakta. Om vi har ett golv med en fast temperatur så kommer gasen efter ett tag att ha exakt den temperaturen (men tills dess så kommer vi ha en gradient). Låter vi golvet hela tiden värma gasen, oavsett vilken temperatur den har, så kommer vi alltid ha en gradient men temperaturen kommer då att öka hela tiden.
I din simulering – är det inte ett av dessa fall du ser?
Det samma gäller om vi har en dag/natt. Låt oss anta att vi börjar i ett system där vi har en gradient – som vi efter ett dygn skall återkomma till. Under dagen får vi naturligtvis en ökad gradient men vad händer under natten? Vi kyler av gasen närmast golvet så att vi får en negativ gradient närmast golvet. De varmare lagren högre upp kommer dock sprida sin värme både uppåt och nedåt vilket gör att det översta lagret får en högre temperatur. Hur skulle vi kunna komma tillbaks till den ursprungliga gradienten? Om natten avslutas för tidigt så har vi visserligen en gradient men temperaturen i det översta lagret har ökat.
Hur ser det ut i dina simuleringar, är systemet adiabatiskt dvs ingen energi tillförs?
#153 Johan M
Glem den med inget tak, min fejl.
”Ergo – orsaken till att vi har en gradient är inte gravitationen utan det kalla taket och varma golvet. Gradientens utseende påverkas av gravitationen.”
Uden varme kulde har du alligevel en trykgradient selvom temperaturen bliver ens. Derfra kommer min tvivl.
Alle de partikler som befinder sig i bunden må have fået et tilskud fra gravitationen, da de startede midtvejs. Partiklerne i toppen må tilsvarende have mistet noget til gravitationen. Det burde give anledning til en temperaturgradient, som ikke viser sig i din model.
Du nævner selv sammenstødene som en årsag, og der tror jeg også noget af svaret ligger.
Sammenstødene virker som en diffusion (som varmeledning). Hvis denne diffusion er meget større end tyngdekraftens virkning i din model, så er resultatet næsten givet.
Kan du overveje om diffusionen i din model har et realistisk forhold til tyngdekraften?
#155 Johan M:
Tack för tipsen, jag ska dubbel- och trippelkolla allt. Det låter rimligt att ändläget är isotermt om golvet har konstant temperatur.
Men vad gäller dag/natt-varianten så tror jag att ditt golv har för stora temperatursvängningar vilket vänder upp och ned på gradienten nattetid. Kan du prova med en mindre amplitud?
Det bör då bli nästan samma sak som en konstant golvtemperatur men gasen kan aldrig bli isoterm eftersom den jagar ett ”rörligt mål”.
Men jag är helt öppen för möjligheten att jag har gjort något fel i mina beräkningar, återkommer…
Temperatur under gravitation.
Johan M og hans model ser ud til at være korrekt efter læsning af min gamle varmelære af E. S. Johansen.
Molekulernes kinetiske energi i et tyngdefelt, side 252.
Årsagen skyldes Maxwll-Boltzmann’s fordelingslov!
Han skriver også at man let kan tage fejl, som jeg og andre har gjort.
Original udgaven er fra 1954.
Hvad det så betyder for klimagasser og global temperatur er stadig til diskussion.
Temperaturgradienten på planeter hvor vi kender den følger tæt teorien med tyngdekraften.
Det gælder Venus, Jorden og Mars, som har vidt forskellige atmosfæresammensætninger og temperaturer.
Det var godt at Johan M tog emnet op, så det blev afklaret.
Johan M:
OK, efter att ha förbättrat den numeriska stabiliteten så får jag nu exakt samma resultat som du.
Det blir isotermiska ändlägen (eller i vart fall ingen tydlig gradient) oavsett om golvet har en fast temperatur eller om denna varierar cykliskt över ”dygnet”.
Om jag däremot lägger till en liten kontinuerlig avkylning av partiklarna så dyker gradienten upp med ”golvvärme på”. Detta skulle motsvara en viss inblandning av växthusgaser eller ev. att alla gasmolekyler i någon mån kan kylas radiativt.
Intressant!
#159 KM
Skönt att du kom fram till samma slutsats ( nu kan jag sova
Jag håller på och leker med Elm (språk som kompilerat till javaScript) och tänkte porta simulatorn så att man kan köra egna experiment i en browser. Har fått cirklar att röra sig på skärmen så är en bit på vägen