Detta ämne har ju diskuterats här ganska flitigt alltsedan Gösta’s första inlägg här i våras. Samlingen av inlägg ges av följande länk till bloggens sökfunktion. Jag hade ambitionen att söka illustrera sakfrågan med några simuleringar, men har fastnat på någon för mig dold formalism eller bugg för just ”compartmental kinetics” i det allmänt tillgängliga dataprogram jag använt mig av.
Men principerna förblir desamma. ”Bernkurvan”, som en bas för påståenden om att ”koldioxiden stannar i atmosfären i hundratals år”, synes för mig själv fysikaliskt omöjlig.
Det är i linje med vad Gösta hävdar, och är i så fall mycket allvarligt, eftersom ovanstående påstående är en hörnsten för klimatalarmismen.
Först kanske vi bör erinra oss att kemisk kinetik har sin bas i ett eller flera sannolikhetsförlopp – reaktionshastigheten i en viss riktning är proportionell mot
(hastighetskonstanten för reaktionen) x (koncentrationen av en viss reaktant)
Reaktionshastigheten i motsatt riktning ges p.s.s. av
(hastighetskonstanten för den återgående reaktionen) x (koncentrationen av reaktionsprodukten)
Observera att det i sammanhanget gäller koncentrationer – inte mängder. (Undantag är behandlingen av ”compartmental kinetics” – utbyte av komponenter mellan avgänsade ”behållare”, som exempelvis levande celler och omgivande vätska. Där inför man för att göra modelleringen mer smidig ”koncentrationer av reaktanter och produkter” genom att ange deras mängder tillsammans med volymer av de olika ”compartments”).
Vid kemisk jämvikt är reaktionshastigheterna i båda riktningar lika stora, och vi har det enkla sambandet:
Jämviktskonstanten för förloppet = Kvoten mellan nämnda hastighetskonstanter
som givetvis också båda är temperaturberoende – liksom då jämviktskonstanten. Någon kanske nu associerar till begreppet ”massverkans lag”, som man på min tid fick serverat på grundskolenivå.
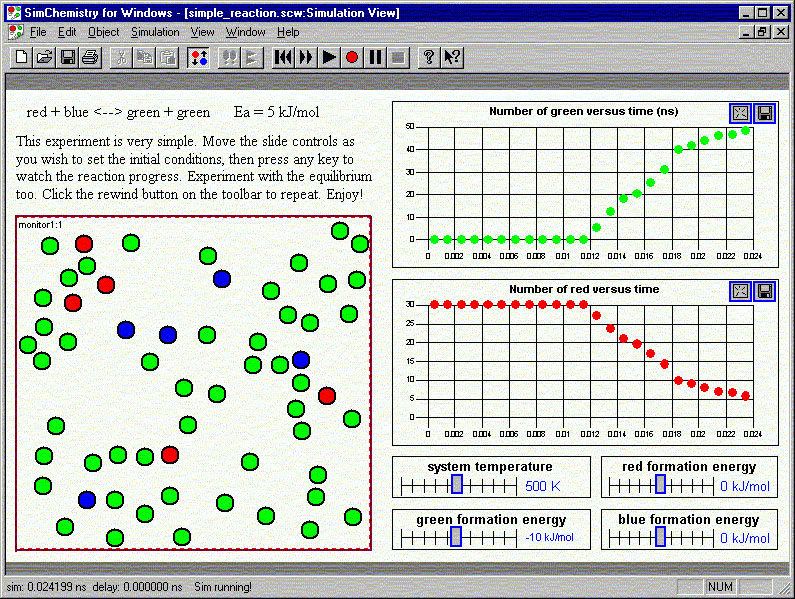
Sakens underliggande statistiska natur framstår klart om man roar sig med att köra följande undervisningsdataprogram, där reaktionshastigheter och jämviktskonstanter för att skapa ”gröna bollar” ur ”röda och blå” via molekylkollisioner modelleras helt statistiskt som processer med viss sannolikhet. I gränsfallet extremt många ”bollar” ( 1mol är ju nästan 10^24 stycken) blir behandlingen exakt, och ansatsen har faktiskt använts forskningsmässigt i sammanhanget.
Men det vanliga är att som nedan lösa ett system av modellbeskrivande kopplade differentialekvationer numeriskt. Det tar vanligen mindre än en sekund på en vanlig PC, även för mycket mer komplicerade system.
I det fall vi närmast betraktar (utbyte av koldioxid, primärt mellan atmosfär, havsvatten och biosfär) är det egentligen fråga om ”compartmental kinetics” och en mångfald komplicerande ytterligare faktorer, men jag illustrerar i det följande ett mycket förenklat åskådningsfall där kemisk kinetik och jämviktsinställning modelleras i en gemensam behållare.
Den egentliga sakfrågan förblir densamma – hur uppför sig en snabb utbytesreaktion mellan två låtsastillstånd (koldioxid i atmosfär, respektive ytlager), kopplat till ett tredje låtsastillstånd (djuphav) med väsentligen mycket längre jämviktsinställning (mellan ytlager och djuphav) och större volym?
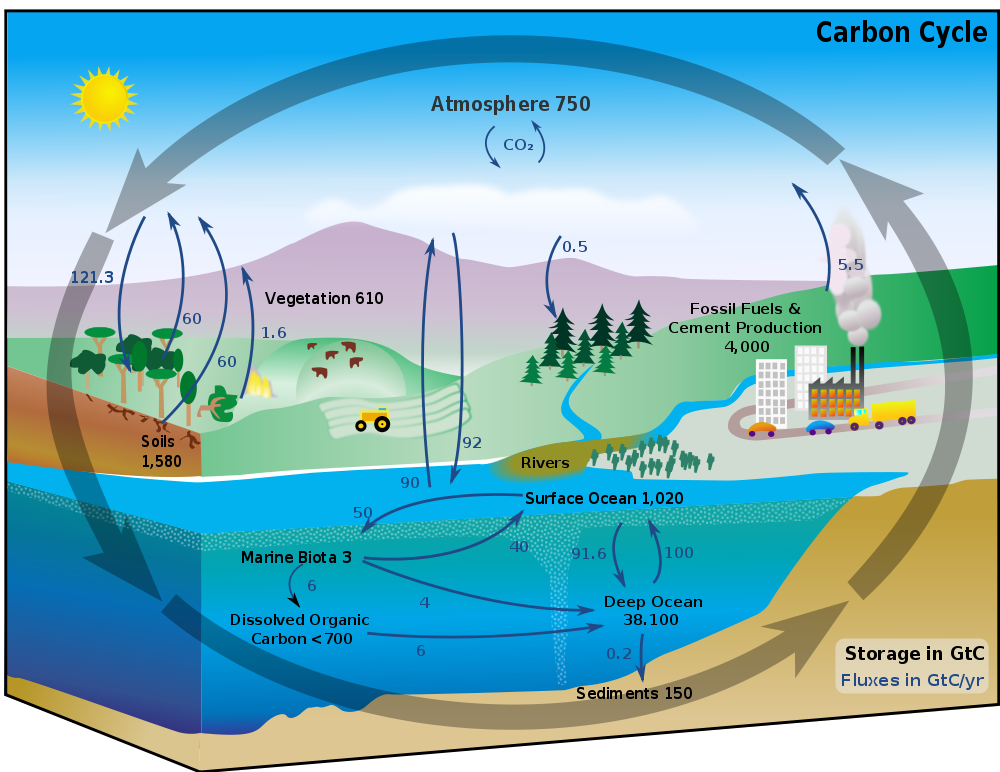
Ja, det är mycket förenklat – något mer fullständigt skulle det se ut så här (just denna bild är tagen härifrån – det finns åtskilliga att finna via en bildsökning på webben)
I vårt enkla åskådningsexempel är sen hastigheterna för omsättningen mellan de olika reservoarerna (pilarna i diagrammet ovan) det viktiga för de sakfrågor kontroversen gäller. Samma sannolikhetslagar som i annan kemisk kinetik verkar i botten, och det gäller att nu söka analysera konsekvenserna av dem.
Låt oss utgå från ett fall där ”atmosfären” innehåller ”1” koncentrationsenhet koldioxid, som står i jämvikt med ”ythavet”, och i sin tur ”djuphavet”, som båda innehåller ”10” enheter. Vi antar också att ”ythavet” och ”djuphavet” är i jämvikt.
Vad är nu de relevanta hastighetskonstanterna? Den första – för transport mellan atmosfär och djuphav – ges faktiskt direkt av ”bombprovskurvan” (och flera andra uppskattningar, bl.a. av Bertil Bolin, redan på 1950-talet), som avklingar på i storleksordningen 10 år. Låt oss anta att den sker på ca 5 år och att hastighetskonstanten i exemplet nedan då kan sättas till 0.2 / år.
För jämvikt med ytlagret måste därför den återgående reaktionshastigheten vara 0.02 / år. Och för att få jämvikt mellan ytlager och djuphav i åskådningsexemplet måste ifrågavarande hastighetskonstanter vara lika, låt oss sätta dem till 0.0002 / år – d.v.s. ett par tiopotenser långsammare än dem vid havsytan.
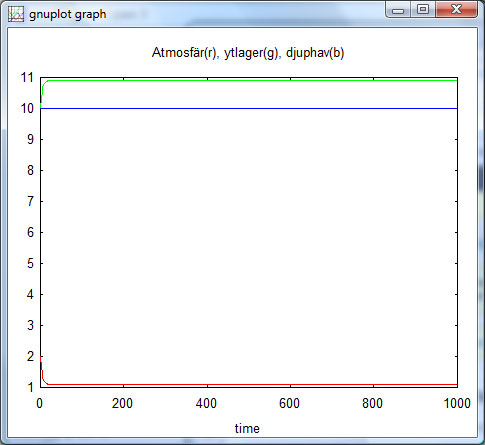
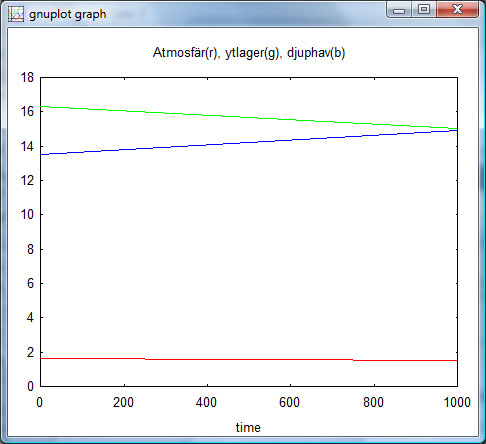
En graf över 1000 år, med ”koncentrationerna” på y-axeln bekräftar att det är jämvikt (linjerna för ythav och djuphav överlappar, så bara den ena syns):
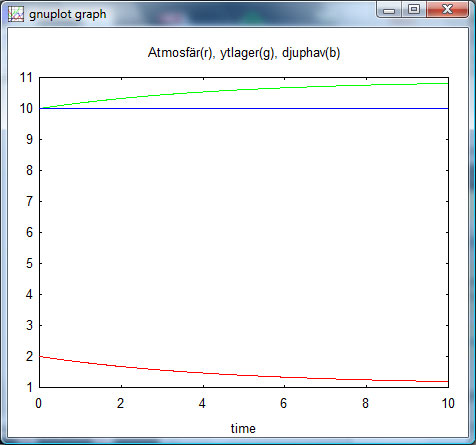
Lägg nu på en ”puls” av koldioxid i atmosfären, motsvarande en fördubbling av koncentrationen:
Expanderat de första 10 åren ser det ut så här:
Som synes händer i denna modell ”ingenting” med djuphavens koldioxidinnehåll under 1000 år. Atmosfärens och ytlagrets koldioxidinnehåll går mot asymptotiska värden motsvarande tillskottet av koldioxid till hela systemet.
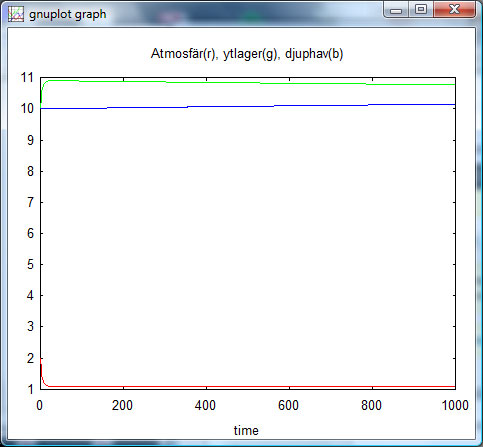
Låt oss nu göra jämvikten mellan djuphav och ythav 10 ggr snabbare, motsvarande en hastighetskonstant på 0.002 / år, och expanderar åter till 1000 år:
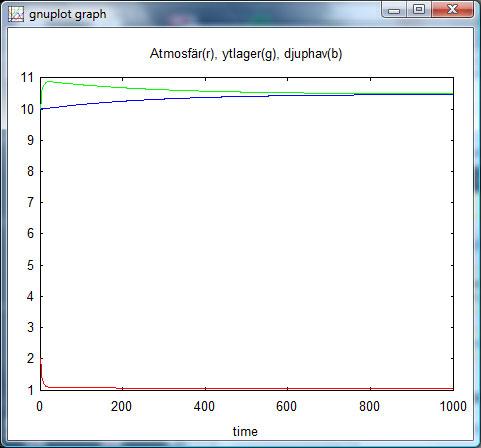
Nu börjar till slut något hända med djuphavets kurva. Vi prövar att göra ”djuphavshastighetskonstanten” ytterligare 10 ggr snabbare:
Jaha. Fördröjningen ligger vid aktuell situation ”helt” i djuphavet.
(En närmare analys av den röda kurvan visar att den inte är monoexponentiell utan biexponentiell, och att den snabba komponenten ligger nära (men är inte lika med 0.2 som var hastighetskonstanten för dess försvinnande). Den långsamma komponenten är p.s.s. ”lånad” från den långsammare djuphavsprocessen. Men vi fördjupar oss inte i det.)
Låt oss nu lägga på en ”ramp” istället för en puls, vad gäller tillskottet till atmosfären – uppskattningar ligger i dagsläget på drygt ca 1% bidrag från fossilförbränning per år till existerande mängd. Vi antar för enkelhets skull 1%, och återställer nu atmosfärens koncentration till ”1” koncentrationsenhet:
Slutvärdena för koncentrationerna efter 1000 år är i tur och ordning ca 1.6, 13.5 och 16. Låt oss se vad som händer om man plötsligt stoppar ”fossilförbränningen”:
Jag upprepar för tydlighets skull att det hela bara är tänkt som en illustration av kemiskt kinetiska principer och uppförande, med koldioxidomsättningens kontroverser som bakgrundsassociation.
a) Om ”ytlager” och ”djuphav” är ”överladdade” jämfört med tillstånden motsvarande kemisk jämvikt får man givetvis en långsam återgång till jämvikt även i atmosfären, men det beror inte på att ”koldioxiden stannar i atmosfären” utan på att den tillförs från haven.
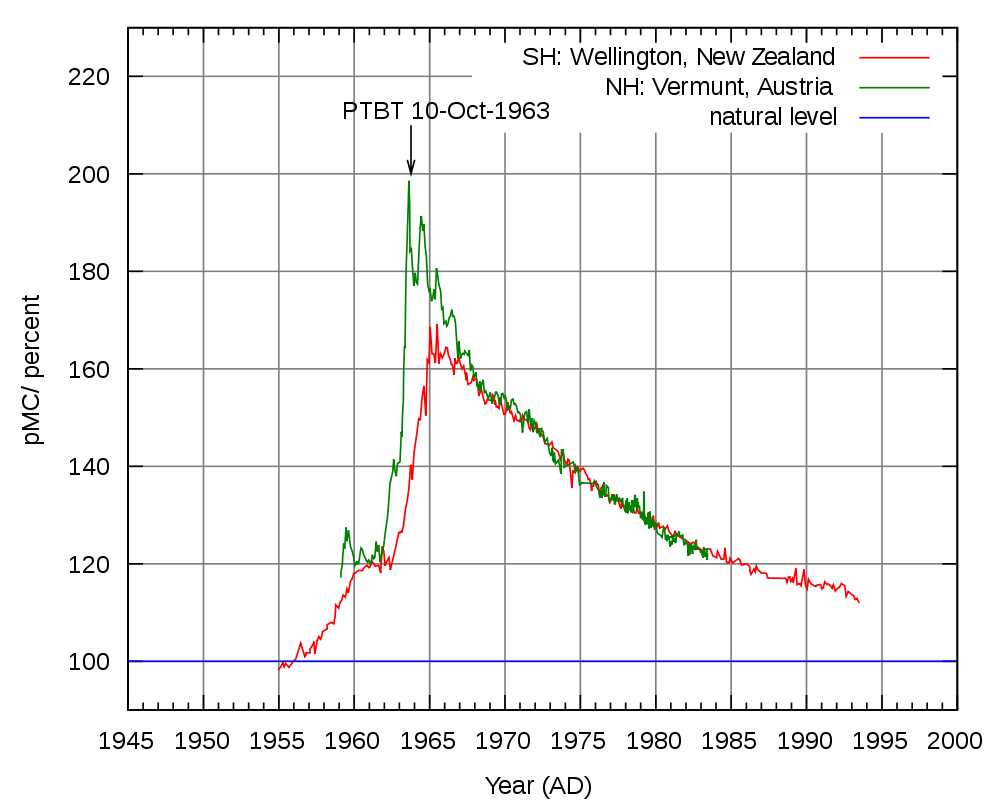
b) I den nära bloggvärlden har framförts att ”Bombkurvan” inte har ”noll” som baslinje, utan snarare går från ett värde på ca 100 någonting till 200 någonting och sen avklingar exponentiellt till 100 – som är något slags ”steady-state” i atmosfären för C-14 genom relativt konstant påverkan (på N-14) av kosmisk strålning.
Allt implicerande att Gösta har fel/missuppfattat. Det har han nu inte, och argumentet saknar ändå betydelse för den egentliga sakfrågan – trots marginella korrektioner (som också diskuterats av Gösta) är avklingningen av C-14 till denna approximativa stady-statenivå fortsatt karakteriserat av en hastighetskonstant motsvarande livslängden (i storleksordningen 10 år) för en enskild koldioxidmolekyl i atmosfären (som slutligen tas upp av biomassa, världshaven eller vittring).
(bild från Wikipedia)
c) Vore det inte för ”Revellefaktorn” skulle det skilja ytterligare en faktor ca 10 i fördelningen mellan atmosfär och hav (som mellan koldioxidhaltig luft och destillerat vatten, där partitionsjämvikten enligt Henry’s Lag ligger på ca 1 del i luft och 50 i vatten). Revellefaktorn kommer inte in på annat sätt i resonemanget, eftersom den (experimentella) livslängden för en koldioxidmolekyl i atmosfären redan inkluderar dess effekt.
d) Givetvis är allt ovanstående mycket förenklat, och jag skulle kunna räkna upp ett 20-tal saker som inte nämnts, eller modellerats in. Haven är dessutom aldrig ens i jämvikt pga temperaturvariationer, skiktning och varierande tryck och strömning mellan dessa – vilket påverkar ”jämvikter” såväl som kinetik. Vi har också kontinuerlig tillförsel av nederbörd – direkt, eller via floder. Parallellt med haven har vi också växtligheten på land och organismer i hav som väsentliga pooler i kolomsättningen på Jorden. Men principerna och det allmänna beteendet för kemiskt kinetiska processer förblir detsamma.
e) Slutligen – det finns tydligen inte så mycket fossilt material på Jorden att man inte ens kan komma upp en fördubbling av koldioxidhalten i atmosfären (alltså ca 600 ppm) – en höjningsnivå, som av många hävdas motsvara en en temperaturhöjning på ca 1 grad, om man bortser från effekten av allt sot som skulle komma ut från de mängdmässigt dominerande fyndigheterna av stenkol.
Ja, nog finns det värre saker att oroa sig för.
Jag är säker på att både Gösta och Pehr kan och vill komma med kompletterande synpunkter.
Professor emeritus i Fysikalisk Kemi vid KTH. Klimatdebattör sedan 2003.


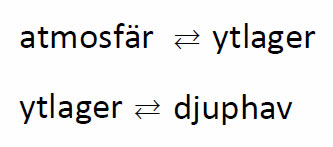








Tack Peter,
jag hoppas att du ser att det du gör här är ungefär detsamma (fast mer pedagogiskt upplagt) som jag har gjort i mina räkningar – de där huvudpunkten är en jämförelse mellan effekten av att fortsätta att använda fossilt kol och att övergå till bio-bränslen. Det som händer när man har mer fler ”compartments” är att man får fler egenvärden, varvid det ”dominerande” är det som har att göra med den kortaste omloppstiden.
Och när får vi se en artikel med er (Peter, Pehr och Gösta) med Gösta som huvudförfattare insänt till Climate eller Journal of Climate, JGR, Climate Dynamics eller någon av de andra mer seriösa tidskrifterna? (Strunta i Nature eller Science, det skulle bara dra ned er trovärdighet :-))
Ingemar,
Det låter osannolikt att det blir en artikel, eftersom Pehr är den ende av de 3 som verkar förstå Revelleeffekten. Kanske vore bra om han förklarade för dom övriga? Är ju bra om man förstår något av ämnet man skall publicera inom.
Vi som kritiserat Gösta et al är helt med på Peters enkla post, vilket är kinetik enligt första kapitlet i grundkursen. MEN: utöver detta tillkommer Revelleeffekten, vilken man inte utan skäl bara kan negligera.
Jonas B1 #3 – jag kommenterar Revellefaktorn i fotnoten c) mot slutet
Peter #4,
Jo, jag såg det. Jag kan inte tolka det stycket på annat sätt än att du missförstått Revelleeffekten, vilken gör att svaren inte blir så enkla som du här visar. Det är karbonatjämvikten som gör att havet innehåller mycket mer C än vad Henrys lag skulle ge, inte Revelleffekten.
Om Revelleeffekten gäller så ger den en Bernkurva för ett stort CO2-utsläpp.
Bombexperimentet däremot ger ingen Revelleeffekt utan där har vi simpel blandning enligt din beskrivning, vilket ger bombkurvan helt enligt förväntan (förutom möjligen på slutet en ev urskiljbar ökning pga antropogent C12, men det är inte poängen här).
Om inte jag minns helt fel så är Bernmodellens långa uppehållstid en funktion av att de förutsätter en rejäl temperaturuppgång på grund av höjd CO2 nivå. Den förhöjda temperaturen är huvudorsaken till att CO2 får en extremt lång uppehållstid då den antagna temperaturhöjningen etablerar en annan balanspunkt och håller kvar CO2 nivån på en hög nivå.
Dvs de är också av uppfattningen att temperaturen styr CO2 nivån.
Jag ser det mer som cirkelargumentation från Bernmodellens upphovsmän.
Det som skiljer åt är uppfattningen om hur mycket CO2 ändrar temperaturen uppåt.
Klimatkänsligheten igen alltså.
Jonas B1 #5 – nu förstår jag inte vad Du menar – ”The Revelle factor is a measure of the resistance to atmospheric carbon dioxide being absorbed by the ocean surface layer posed by bicarbonate chemistry. It is named after the oceanographer Roger Revelle.” – enligt Wikipedia
Förklara gärna ”e) Slutligen – det finns tydligen inte så mycket fossilt material på Jorden att man inte ens kan komma upp en fördubbling av koldioxidhalten i atmosfären (alltså ca 600 ppm) – en ”
Jorden har haft enormt högre CO2-nivåer än idag. Var skulle detta kol ha tagit vägen?
Jarek #8.
Bra fråga.
Kalksten CaCO3 ?!
Kan vara värt att påpeka att den blå kurvan i första diagrammet ovan inte har något med vad Bernmodellen förutsäger. Pehr har i sina inlägg varit betydligt mer korrekt.
Jarek #8 – Jorden hade (tror man) ca 80% koldioxid i atmosfären en gång (resten kväve och vattenånga). (Liksom på Venus). När sen växtlivet började konsumerades koldioxid via fotosyntesen, och syre skapades.
Nu har vi istället ca 20% syre och 400 miljondelar koldioxid. Ja, nästan all koldioxid är mineraliserad, som Bengt #10 redan påpekat. Jag vet inte siffran, men säg >99%.
En liten del kol föreligger som kol och råolja och metangas etc.
Jarek Luberek #8, Åke N #9, Bengt Abelsson #19
Kolet har fossiliserats i form av torv, brunkol, stenkol, olja, kalksten och krita.
Se t. ex. Kapitel 12 i http://www.falskt-alarm.se
Thomas P #11
Diagrammets blå kurva är den ”impulse response function” (relaxationsfunktion) som förutsägs av Bernmodellen och som modellens konstruktörer (bl. a. av ekonomiska skäl) rekommenderar externa forskare att nyttja sig av som en förenklad version av den fullständiga modellen för kalkyler av bidrag från utsläpp av fossil koldioxid till luftens koldioxidhalt.
Blå kurva representerar den relaxationsfunktion IPCC specificerade för Bernmodellen och använde sig av i 2007-års rapport.
Gösta #14 Den blå kurvan motsvarar relaxationstiden för ett tillskott av CO2 i atmosfären, inte för en puls av C-14. Skillnaden har ältats här i otaliga inlägg, och om du inte förstått den än fråga Pehr, du kanske respekterar honom mer än mig. Jämför t ex din och Pehrs kurvor i detta inlägg:
https://www.klimatupplysningen.se/2013/06/14/bombkurvan-igen-modell-och-observationer-stammer-inte/#.UlmpKhC1t9g
Thomas P #15
Blå kurva har bestämts av Joos et al. som svaret på ett pulsmässigt tillskott av CO2 enligt Bernmodellen, vilken (enligt gängs kinetisk praxis) förutsätter att alla CO2-isotoper uppvisar samma kinetiska beteende.
Därför är blå kurva även representativ för relaxationen av ett pulsmässigt tillskott av 14CO2.
Jag kan inte finna något i Pehrs inlägg som tyder på att han har en annan syn än mig i det avseendet.
Thomas P #15
Mitt svar i #16 hamnade nog vid sidan av vad du förmodligen anser vara kärnproblemet, dvs att Bernmodellen tagit hänsyn till Revelleeffekten som triggar en pH-ändring, medan pulser av 14CO2 är så små att de inte triggar någon pH-ändring.
Men som Pehr påpekar skulle en pH-ändring triggad av CO2 även ha påverkat bombprovskurvan. Och när man inte ser någon påverkan på bombprovskurvan, så är den enklaste förklaringen att Revelleffekten inte är stark nog att åstadkomma någon påverkan.
Och kärnpunkten i mitt resonemang är att Bernmodellens relaxationsfunktion (blå kurva), oavsett hur den kalkylerats, är gravt undermålig som beskrivning av den observerade kinetiken för relaxationen av ett överskott av koldioxid.
På måndag kan du troligen läsa ett TCS-inlägg från mig som visar att koldioxidens uppehållstid kan beräknas till 14 år med en metod som utgår från Keelingkurvan med dess El Niño-fluktuationer och därmed inte involverar 14CO2 över huvud taget.
Thomas #15,
Jag håller med Gösta att den blå kurvan är en pulsresponsfunktion.
I själva verket ser den ut att vara nästan identisk med en av kurvorna i figur 1 i en artikel av Joos med flera från 1996 i Tellus:
http://www.climate.unibe.ch/~joos/papers/joos96telb.pdf
Uppenbarligen menar man att svaret på en momentan fördubbling av koldioxidhalten i atmosfären är en pulsresponsfunktion.
Figurtexten talar om pulsresponsfunktioner för HILDA-modellen och detta är oceankomponenten i Bernmodellen om jag förstått texten i artikeln rätt. Gösta har tidigare kommenterat om sambandet mellan HILDA och Bernmodellen.
#18 fortsättning:
En intressant fråga som slog mig när jag läste inledningen till artikeln av Joos med flera i Tellus 1996 enligt länken ovan är vad som händer i och med att temperaturen ändrar sig.
Författarna bygger på att man kan beräkna hur koldioxiden tas upp genom en att använda sig av en pulsresponsfunktion som integreras tillsammans med hur utsläppen av koldioxid varierat med tiden.
Men detta fungerar om man kan anta att de processer som beskriver hur koldioxiden tas upp från atmosfären är matematiskt linjära.
Vad författarna då tycks ha förbisett är att vi lever i en era då jordens globala temperatur ändrar sig. Temperaturändringen ändrar parametervärdena i de linjära processerna så att det resulterande förloppet för upptag av koldioxiden inte längre blir linjärt.
Göstas enkla modell tar däremot hänsyn till detta, den beskriver de olinjära processer som beror på temperaturen med hjälp av Arrhenius ekvation.
Forvirret
Bombprovskurvan fortæller vel kun hvor længe et et givent CO2 molekyle opholder sig i atmosfæren før det eventuelt skiftes ud med et andet (fra havet mest sandsynligt).
Den kan ikke fotælle noget som helst om hvordan den totale koncentration udvikler sig, men vel egentlig kun fortælle om udvekslingen mellem atmosfæren og diverse depoter.
Den menneskeskabte udledning af CO2 er i alle fald mindre end 10% af den totale omsætning.
Jeg er i tvivl om hvad Bernmodellen egentlig prøver at fortælle, men fornemmer at det ikke er helt ligetil at vurdere hvor ligevægten ligger mellem depoterne og atmosfærens indhold af CO2.
Meget tyder også på, at CO2 slet ikke har den virkning som det er blevet tilskrevet, hvorfor denne CO2 udveksling mere er af akademisk interesse end reel i forhold til temperaturen.
Har jeg misforstået noget?
Svend Ferdinandsen #20
Bombprovskurrvan visar enligt vilket förlopp (monoexponentiellt) och med vilken tidskonstant (14 år) ett överskott av CO2 bortskaffas ur atmosfären. Dessa data krävs för att man ska kunna beräkna hur mycket antropogena utsläpp av CO2 bidrar till att öka luftens koldioxidhalt.
Se Paper 1–3 på http://www.false-alarm.net, vilka föranlett Peter Stilbs inlägg.
Hvis du mäktar med svenska språket kan du även pröva att läsa boken http://www.falskt-alarm.se, speciellt kapitel 7–8.
Gösta och Pehr Ni säger båda att ni är överens, men ändå skiljer sig figurerna i Pehrs tidigare inlägg åt dramatiskt något som jag inte sett att någon av er egentligen tar itu med att förklara:
https://www.klimatupplysningen.se/2013/06/14/bombkurvan-igen-modell-och-observationer-stammer-inte/#.Ulo_CxC1t9h
”Men som Pehr påpekar skulle en pH-ändring triggad av CO2 även ha påverkat bombprovskurvan. ”
Vad Pehr tidigare påpekat är att C-14 halten först avtar snabbt men sedan skall börja öka en aningen igen, något som möjligen kan bli detekterbart så småningom (se figur 2 i min länk), men givet att naturlig produktion av C-14 varierar m m blir detta inte lätt att urskilja. Detta är något helt annat än din blå kurva som inte har något att göra med hur Bernmodellen förutsäger att en C-14 puls skall avklinga.
Just nu verkar Pehr däremot fått för sig att det trots allt är GP:s blå kurva som är förväntad respons för en C-14 puls i strid med vad han tidigare sagt. Det blir allt mer obegripligt vad ni kemister egentligen anser.
Apropå Revelleeffekten så har DN idag en ny skrämselartikel om CO2 och haven.
http://www.dn.se/nyheter/vetenskap/surare-hav-hotar-hela-ekosystem/
”Våra utsläpp av koldioxid gör inte bara jorden varmare. De försurar också haven, med förödande konsekvenser.
….
Försurningen märks i alla världens hav. Vattnet har blivit nästan 30 procent surare sedan industrialiseringen började. Om utsläppen fortsätter att öka som nu kan det vara dubbelt så surt vid seklets slut.”
Skrämselartikeln är skriven av en ex-kreationist. Kanske hon också kommer revidera sin syn på AGW med tiden. Med det är kanske att hoppas på för mycket då hon har tidigare fått svidande kritik för ensidig rapportering = vinkling, av vetenskapliga forskning.
http://www.dn.se/debatt/er-ohederliga-journalistik-skadar-mig-som-forskare/
http://www.fritanke.se/maria-gunther-axelsson-en-ex-kreationist-talar-ut/
Gösta,
”Men som Pehr påpekar skulle en pH-ändring triggad av CO2 även ha påverkat bombprovskurvan.”
Ja, men på ett fullständigt annat sätt än du länge hävdat. Och det är högst tveksamt om det sättet överhuvudtaget är detekterbart, beroende på varierande C14 produktion, exakt definition av C14-halt, verklig storlek på Revellefaktor etc. Du ger oss kritiker helt rätt utan att erkänna tydligt.
Thomas #22,
Du har förbisett skillnaden mellan det Gösta gjort och det jag gjort i mitt blogginlägg:
https://www.klimatupplysningen.se/2013/06/14/bombkurvan-igen-modell-och-observationer-stammer-inte/#.Ulo_CxC1t9h
Jag har där beräknat hur bombkurvan borde se ut enligt Bolins och Erikssons (1959) teori.
Gösta har däremot undersökt hur bombkurvan i realiteten ser ut. Göstas resultat innebär alltså att bombkurvan inte följer Bolins och Erikssons teori enligt min beräkning.
Den kurva som Gösta kallar Bernkurvan är förmodligen samma kurva som Joos med flera (1993) i figur 1 anger som pulssvar på en fördubblad koldioxidhalt. I samma figur anger de hur ett pulssvar för en ändrad kol-14 halt borde se ut, men har då inte tagit hänsyn till inverkan av ändrad koldioxidhalt i atmosfären på grund av utsläpp av fossil koldioxid under tiden pulssvaret utvecklas. Det har däremot jag gjort i mitt blogginlägg.
Vi ser från denna figur att även utan effekten från utsläppen av fossil koldioxid så blir pulssvaret för kol-14 annorlunda än den kurva som Gösta har kommit fram till.
Sedan är det också så att Göstas modell, oavsett hur bombkurvan ser ut, beskriver observerade data på ett anmärkningsvärt bra sätt. Det är detta som jag har bekräftat i mitt blogginlägg:
https://www.klimatupplysningen.se/2013/09/20/koldioxidmodellerna-revideras-fran-ruta-ett-gosta-pettersson/#.UlqcLilvlis
De värden på hastighetskonstanterna som han använder överensstämmer väl med vad IPCC anger för dessa. Det som gör Göstas modell unik är införandet av temperaturberoendet i hastighetskonstanten för utgasning från havet med hjälp av Arrhenius ekvation.
Om du inte läser in de olika vetenskapliga artiklarrna som vi bygger på kan du knappast räkna med att få en djupare förståelse av detta. Jag förstår inte varför du bara vill uppträda som nejsägare i stället för att studera området och komma med mer konstruktiv kritik.
Pehr #25 ”Den kurva som Gösta kallar Bernkurvan är förmodligen samma kurva som Joos med flera (1993) i figur 1 anger som pulssvar på en fördubblad koldioxidhalt.”
Detta är alltså FEL som beskrivning av hur en C-14 puls avklingar. Detta vet du uppenbarligen egentligen även om du inte klarar av att säga rätt ut att Gösta har fel. Den kurva du istället räknat dig fram till är inte möjlig att skilja från mätdata.
” Jag förstår inte varför du bara vill uppträda som nejsägare i stället för att studera området och komma med mer konstruktiv kritik.”
Jag uppträder som nejsägare för att främst Gösta men i mindre mån även du så klart visar att ni har fel vilket båda jag och Jonas B1 finner värt att upprepa. Jag har för egen del inga ambitioner att försöka skapa en realistisk modell för kolcykeln eftersom jag inser hur mycket jobb det är om man skall vara just realistisk.
Stickan no 1,
Tack för intressant information. När man läser sådant undrar man verkligen vad som kan pågå i en del människors huvuden. Det finns förmodligen tankebanor som är så känslostyrda och irrationella att de inte går att förstå av andra och i efterhand.
Thomas #26,
Bernkurvan kan i princip avse avklingningen av 14C. Det gör ingen skillnad om pulsen består av 14C eller 12C. Bernkurvan utmärker sig för att mängden i pulsen motsvarar fördubblad koldioxidhalt.
Den bombkurva som Joos med flera (1993) visar i figur 1 är beräknad med samma Bernmodell som den som ger den Bernkurva de visar i samma figur.
http://www.climate.unibe.ch/~joos/papers/joos96telb.pdf
Denna beräknade bombkurva avklingar snabbare därför att mängden i pulsen är extremt liten jämfört med Bernkurvan ovanför. Men det är en kurva som följer precis samma modell och som visar samma karakteristiska form, dvs. en flerfasig exponentiell kurva.
Gösta har påpekat att den verkliga bombkurvan inte uppvisar en sådan flerfasig form. Den överensstämmer alltså inte med den bombkurva som Joos med fler (1993) har beräknat med sin Bernmodell.
Jag kan inte se annat än att det skiljer mellan den verkliga bombkurvan och den bombkurva som Joos med flera (1993) har beräknat.
Det är väl detta som är det viktiga. Jag upplever att det blir en diskussion om någon slags formaliteter som är helt betydelselösa. Frågan här är om den verkliga bombkurvan överensstämmer med Bernmodellen eller inte. Hur man än vänder och vrider på detta, med de litteraturreferenser som vi har tillgängliga så här långt i diskussionen, blir resultatet att Bernmodellen inte överensstämmer med den verkliga bombkurvan.
Detta kan säkert diskuteras djupare än vi gjort här men vi lär inte komma framåt i diskussionen genom semantiska utvikningar.
Pehr #27 ”När man läser sådant undrar man verkligen vad som kan pågå i en del människors huvuden. Det finns förmodligen tankebanor som är så känslostyrda och irrationella att de inte går att förstå av andra och i efterhand.”
Och du som brukar bli så upprörd när någon av dina favoriter utsätts får någon form av ad homimen. Varken du eller Stickan no1 gör minsta försök att bemöta i sak. Stickan lyckas hitta att författaren en gång var kreationist även om hon insett felen i detta och du kör ett rent personangrepp.
”Bernkurvan kan i princip avse avklingningen av 14C. Det gör ingen skillnad om pulsen består av 14C eller 12C. ”
Är du där nu igen? Skall det vara så omöjligt att förstå att det är skillnad på C-14 där halten i haven är mycket låg så att man bara mäter flödet ned i haven och C-12 där man mäter nettoskillnaden mellan flöden till och från atmosfären.
” Hur man än vänder och vrider på detta, med de litteraturreferenser som vi har tillgängliga så här långt i diskussionen, blir resultatet att Bernmodellen inte överensstämmer med den verkliga bombkurvan.”
Vi hade för en tid sedan en referens som visade på hur C-14 halten förväntades sjunka för att börja stiga en aningen in på detta sekel. Detta är den mest relevanta artikeln i sammanhanget och dess kurva är inte möjligt att skilja från mätdata idag. Resultatet blir att den verkliga Bernmodellern överensstämmer med den verkliga bombkurvan, till skillnad från Göstas felaktiga kurva som han kallar Bernmodell.
Thomas #29,
Hur kan det bli personangrepp när man inte angriper någon person? Menar du att min reflektion att människor kan tänka känslomässigt och irrationellt så att det blir oförståeltgt för andra är ett personangrepp?
Pehr #30 Jag undrade just om du skulle kära med försvaret att du inte uttryckligen namngav vem du syftade på även om det av sammanhanget stod helt klart, men tänkte att fullt så patetisk kunde du väl ändå inte vara. Jag hade visst fel.
Thomas #29,
Jag återgav hur Joos med flera (1993) jämför de två kurvorna. Så antingen har de fel eller också har du fel.
De refererar till en publikation av Marin Heimann (1993). De konstaterar att att den andel av utsläppet som stannar i luften är mycket större för antropogen koldioxid än för utsläpp av 14C-koldioxid (kallas isotopic ratio i artikeln, men pulsen består ju av ett tillskott av 14C). Oceanens upptag av koldioxid buffras av havsvattnets kolkemi; den relativa ändringen i partialtrycket för koldioxid är omkring tio gånger högre än den relativa ändringen i koncentrationen av total upplöst oorgamiskt kol. Upplösningen av 14C-koldioxid är däremot inte, eller endast lite, buffrad (allt enligt Bernmodellen).
Inte desto mindre ger Joos med fleras (1993) beräkning av bombkurvan med sin Bernmodell en kurva som visar ett flerfasigt förlopp till skillnad från den verkliga bombkurvan enligt Gösta som jag förutsätter överensstämmer med den kurva som du nämner enligt litteraturen.
Den verkliga bombkurvan verkar nu efter femtio år ha planat ut inom några procent från sitt asymptotiska värde. Den kurva som Joos med flera (1993) har räknat fram ligger långt över asymptoten ännu efter hundra år och ändå mer markant, med en markant negativ lutning, efter femtio år.
Detta liknar verkligen inte den verkliga bombkurvan.
Thomas #31,
Jag ser inte att jag i sammanhanget har syftat på någon särskild person inom den diskuterade rörelsen.
Thomas #29
Vi kan väl låtsas att C14-koldioxid och C12-koldioxid lyder samma kemiska och fysikaliska jämviktslagar. Så låter vi de få och ensamma C14-molekylerna slå följe med en C12-molekyl. C14 vägrar att släppa taget och följer sin C12 i alla hopp och kast. Kan man då inte tänka sig att när man då mäter C14 så får man på köpet hur C12 beter sig?
Det är lite svårt att följa med i debatten på detta tema då det krävs att man sätter sig in i en del litteratur. Vad som dock verkar helt klart är vad TP framhåller i #29. Co2 tillförs atmosfären från haven vilket inte syns om man mäter 14-C.
Hittills har jag svårt att se att IPCCs sätt att resonera är helt galet. Tycker att LB sammanfattade det bra och enkelt.
Gustav #35,
Förindustriellt hade havet ett förhållande 14C/12C som i ytvattnet typiskt var 5% lägre än i atmosfären. I djuphavet var detta förhållande 16% lägre än i atmosfären. Detta framgår i kapitel 1, sidan 12, panel 1.2.1, i en en avancerad lärobok av Sarmiento och Gruber:
http://press.princeton.edu/chapters/s8223.pdf
Bombproven innebar att detta förhållande 14C/12C ökade med 80% i atmosfären, alltså nära en fördubbling.
Detta innebär att det, precis som vid vanlig koldioxid, var nära jämvikt mellan 14C i atmosfären och i havet ytskikt. Att djuphavet hade något lägre sådant förhållande beror på att vattnet blandas om så sakta där så att en del av 14C hinner sönderfalla radioaktivt innan den återkommer till atmosfären (halveringstiden är 5730 år).
Det finns alltså massor av 14C i havet förindustriellt i ungefär samma proportioner mellan atmosfär och hav som för 12C. Så argumentet att det fanns väldigt lite 14C i havet när bombkurvan började avklinga är alltså helt fel.
Ökningen av 14C och dess avklingning liknar väldigt mycket en fördubbling av koldioxiden i atmosfären med sin avklingning, utom att det i fallet 14C är fråga om extremt små mängder jämfört med fördubbling av hela koldioxidmängden.
(Det exempel i boken där uppgifterna hämtats visar för övrigt hur man med hjälp av 14C-halterna kan bestämma flödena för utväxling av vatten mellan ythav och djuphav, siffror som används av IPCC bland andra).
Pehr, #36:
Ok tack för svar. Det du säger hade jag inte en aning om och är värdefull information. Dock märker jag att min kunskapsnivå är på tok för låg i detta ens för att kunna hänga med i turerna. Det möjligen skulle det hjälpa om debatten kunde föras i ett annat medium, exempelvis kunde du, GP, TP och någon UI-människa lägga upp korta presentationer med Hangout eller motsvarande? Att som i nuläget hänvisa till blå kurva på s 58, graf 3 som professor ditten helt har missförstått i kommentaren i tråd blablabla… Ja det är marigt att hänga med.
Har också sett betydligt färre ”lågkvalitativa” kommentarer i trådar som behandlar detta ämne så möjligheten att verkligen komma framåt borde vara stor.
#36
”Så argumentet att det fanns väldigt lite 14C i havet när bombkurvan började avklinga är alltså helt fel.”
Det är inte vad vi säger. Vad vi säger är att förhållandet C14/C12 i havet var lägre än den i luften vid bombproven. Som du skriver var det till och med före bombroven lägre halt i havet. Efter proven byts luftens blandning ut mot blandningen i havet under den årliga cirkulationen. Och – vips – man får en bombkurva. Detta hade hänt även om det inte något totalt överskott kol i atmosfären alls.
Bombkurvan visar hur snabbt ett överskott C14 i atmosfären blandas ut med andra reservoarer, inte ett nettoupptag. Bernkurvan försöker däremot beskriva ett nettoupptag. Två helt olika saker, om än inte fullständigt relaterat (bomkurvan får en liten skjuts om det är ett snabbt nettoupptag samtidigt). Att sätta bombkurvan i samma diagram som Bernkurvan överst i detta inlägg är och förblir tyvärr väldigt förvillande.
Det är möjligt Bernkurvan är fel, men bombrovsresonemanget är en återvändsgränd som nog skrämmer bort fler skeptiker än skapar nya.
Nu blev min senaste kommentar lagd i karantän för att jag skrev ett tecken i mitt namn.
Snälla, snälla SI, fixa tillbaka funktionaliteten vid kommentarsinmatning! Jag orkar inte plita dit namn och e-post vareviga gång.
#38
Ett tecken *fel*… skulle det stått, förstås.
Mats Almgren, Professor Emeritus i fysikalisk kemi vid Uppsala universitet har idiotförklarat Peter, Per och Gösta http://uppsalainitiativet.blogspot.se/2013/06/bombkurvan-vad-visar-den.html resp.
http://uppsalainitiativet.blogspot.se/2013/09/den-seglivade-myten-om-bombkurvan.html. Pratar han i sin frygiska nattmössa eller finns det någon substans i det han säger?
Mats #40,
Mats Almgren skriver på ett sätt som jag upplever insinuant. Han försöker få det att se ut som om Gösta Petterssons omräkning av bombkurvan från den spårämnesenhet som definieras av ekvation 1 på sidan 12 i Sarmiento och Gruber (tryckfel: termerna skall stå i omvänd ordning inom parentesen) till haltenheten mol 14C/mol torr luft skulle vara felaktig:
http://press.princeton.edu/chapters/s8223.pdf
Enligt den enhet som definieras i ekvation 1 var värdet för 14C i den förindustriella atmosfären lika med noll. Men detta innebär som synes av ekvationen att förhållandet 14C/12C var detsamma som i standarden och i detta sammanhang definieras standarden som 14C/12C för den förindustriella atmosfären. Som också framgår där var värdet för 14C i havets ytskikt -50 promille i denna enhet vilket innebär att värdet av 14C/12C i detta havsvatten var 95% av värdet i atmosfären..
Vad halten mol 14C/mol torr luft var förindustriellt är osäkert och samma gäller innan bombproven började. Av vad som sägs i boken förhöll sig mängderna av 14C mellan de olika reservoarerna atmosfär och hav ungefär som för 12C, grovt räknat 1:50 (lite mindre 14C i havet på grund av radioaktivt sönderfall av 14C), men mängden 14C var naturligtvis oerhört mycket mindre än mängden 12C.
Jag kan inte se att Mats Almgren har gett något bevis för sitt påstående om Göstas beräkningar. Det är för övrigt så att om man beräknar tidskonstanten för boxmodellen felaktigt ur en kurva med spårämnesenheten enligt ekvation 1 så blir tidskonstanten för liten, dvs. man beräknar en för lång uppehållstid för de enskilda koldioxidmolekylerna. Så poängen med felet uteblir, det är ju för kort uppehållstid som gör att koldioxiden absorberas för snabbt i beräkningen.
Mats Almgren skriver i sitt inlägg att halten 14C i atmosfären (mol 14C/mol torr luft) skulle ha sjunkit på grund av Süesseffekten. Så är inte fallet, Süesseffekten innebär att förhållandet 14C/12C minskar i atmosfären på grund av att fossil koldioxid som släpps ut av människan inte innehåller 14C. Enligt Bolins och Erikssons (1959) teori ökar samtidigt halten mol4C/mol torr luft beroende på att den av människan utsläppta koldioxiden försurar haven så att en del av den 14CO2 som finns i havet drivs ut och ökar halten 14C i atmosfären (bombproven ändrade förutsättningarna för detta radikalt, 14C tillfördes atmosfären av dessa och därefter följde naturligtvis en minskning av halten i atmosfären när överskottet togs upp av främst havet på längre sikt).
Med tanke på dessa fel är jag tveksam till att Mats Almgren är så insatt i detta ämne som han vill få det att se ut.
Korrektion av #42,
Jag såg nu att det inte var tryckfel i ekvation 1, termerna står i rätt ordning (det fanns en tidigare version med detta tryckfel).
Thomas P #22, #26, #29
”Det blir alltmer obegripligt vad ni kemister egentligen anser”
Vad jag själv anser torde framgå klart av Paper 1–3 i http://www.false-alarm.net. I korthet:
Alla experimentella observationer rörande atmosfärens utbyte av koldioxid beskrivs tillfredsställande av den enkla luft/hav-modell som Revelle-Suess ursprungligen presenterade, är konsistenta med IPCC:s grundläggande jämviktdata för kolcykeln , tyder på att koldioxidens uppehållstid och relaxationstid är i storleksordningen 10 år, och konfirmerar att systemet kinetiskt beter sig precis som man teoretiskt skulle förvänta sig för en praktiskt taget irreversibel överföring av atmosfäriska koldioxidöverskott till en helt dominerande sänka (haven).
Bernmodellens impulse response function (blå kurva) står i strid med sådana experimentella data. Dess i teoretiskt avseende grövsta felaktighet ligger i föreskriften att 22% luftburen CO2 (slutvärdet för blå kurva) står i jämvikt med 78% CO2 i naturen i övrigt, vilket förutsätts ha gällt åtminstone sedan 1958. Motsvarande förindustriella jämviktsandelar var enligt IPCC 1,5% versus 98,5%. Det innebär att Bernmodellen föreskriver att haven innehåller ett enormt överskott av CO2, vilket skulle trigga ett utflöde av koldioxid från haven som skulle få bidragen från antropogena utsläpp och termisk avgasning att helt förblekna. Något sådant utflöde har inte synts till.
Jonas B1 #
”på ett fullständigt annat sätt än du hävdat”
Det enda jag mig veterligt har hävdat är att bombprovskurvan inte uppvisar några påvisbara spår av sådana effekter som du diskuterat. Och jag utgår från observationer. Det jag inte ser har jag ingen anledning att diskutera.
”Du ger oss kritiker helt rätt utan att erkänna tydligt.”
Det skulle aldrig falla mig in att förvägra dig rätten att diskutera vilka effekter du vill. Jag ska tydligt erkänna att du har helt rätt i påståendet att ”det är högst tveksamt om det sättet överhuvudtaget är detekterbart”. Men jag utgår som sagt från observationer. Vad som inte har detekterats, och kanske inte ens är detekterbart, är av ringa intresse för mig.
Christopher e #38
”Vad vi säger är att förhållandet C14/C12 i havet var lägre än den i luften ”
Jag har kommenterat ditt synsätt tidigare, men gör ett nytt försök att klarlägga mitt missnöje med det.
1. Det är fullständigt likgiltigt om förhållandet C14/C12 i havet är mycket högre, likstort eller mycket lägre än i luften. Reaktionsflödena för C14 bestäms enbart av halterna av C14 i luft och hav i enlighet med massverkans lag: d[14C]/dt = -kluft [14Cluft] + khav [14Chav]
Storleken av C12 ingår inte i ekvationen.
2. Lösningen till ekvationen är bombprovskurvans exponentialfunktion. Du har helt rätt i att det uppkommer en sådan bombprovskurva så snart man tillsätter ett överskott av C14 till luften, helt oavsett hur stor totalkoncentration av kol är. Det är det som gör bombprovskurvan så informativt värdefull. VI kan bestämma hastighetskonstanterna i ekvationen genom att vi kan följa C14 separat, helt oberoende av hur mycket C12 det finns i atmosfären eller hur stora utsläppen av C12 varit under mätperioden.
3. Bombprovskurvan återspeglar ett nettoupptag av C14 i naturen, eftersom det som försvunnit från luften befunnits ha kvantitativt överförts till hydrosfären och biosfären.
4. Bernkurvan beskriver INTE ett nettoupptag av CO2 i den reella situationen med kontinuerliga utsläpp, utan beskriver den modellförutsagda relaxationsfunktion för en utsläppspuls som man behöver känna till för att kunna beräkna nettoupptagets storlek i den reella situationen. Bombprovskurvan är oberoende av utsläppen (punkt 2), och ger en direkt uppmätning av relaxationsfunktionen för en utsläppspuls.
Bernkurvan utgör en modellbeskrivning av den relaxationsfunktion som bombprovskurvan åskådliggör, vilket gör det helt befogad att i en figur lämföra Bernkurvan med bombprovskurvan. Samt att påpeka att modellkurvan ger en bedrövligt usel beskrivning av vad som i verkligheten observerats.
Mats #41
Jag siktar på att få möjlighet att bemöta Mats Almgrens synpunkter i ett kommande gästinlägg, förhoppningsvis inom 14 dagar.
Till dess rekommenderar jag dig att ta fasta på Pehr Björnboms svar i #42
Tack för kommentarer, alla.
Oansett alla småkorrektioner så ger ändå bombkurvan direkt information om hastigheten för bortförsel av koldioxid ur atmosfären. Såväl sådan med C-12 och med C-14. Och för ”naturliga” omsättningsprocesser.
Vid ”jämvikt” finns alltså motsatta ”naturliga” processer som tillför lika mycket till atmosfären.
I jämförelse med dessa naturliga tillskott är fossilförbränningens ca 4%, om man tar siffrorna vid pilarna i det färgglada diagrammet om kolcykeln ovan (jag tror dock det är lite gammalt – fossilförbränningen är nog ca 10 Gt per år i dagsläget, vilket jag korrigerat för i siffran 4%)
Peter, #48:
Nu finns det såklart kopplingar mellan diverse parametrar men som jag uppfattat LBs inställning är det inte så intressant med vilken takt CO2 byts mellan olika medier. Det intressanta är vilken CO2-halt som finns i atmosfären och där påverkar såklart de fossila tillskotten. Jag vet att jag är dåligt insatt i denna fråga men jag udnrar ibland lite vart ni vill komma? Såklart kan det vara intressant även att enbart identifiera fel men det kanske i så fall inte är jätteintressant att driva frågan på TCS?
Gustav #49
Det intressanta är inte enbart hur mycket CO2 det finns i atmosfären och hur snabbt halten ökar. Ur samhällelig aspekt är kärnfrågan hur stort ökningsbidrag utsläppen av fossil CO2 ger, eftersom det endast är den delen som kan påverkas av samhälleliga beslut. Och hur stort detta antropogena bidrag är avgörs av koldioxidens uppehållstid.
Då är sakläget det att alla experimentella bestämningar, inklusive bombprovskurvan, tyder på en uppehållstid i storleksordningen 10 år, vilket innebär att utsläppen inte behöver befaras åstadkomma en politiskt oacceptabel ökning av koldioxidhalten. IPCC försöker bortförklara de experimentella resultaten och grundar i stället sina larmrapporter på matematiska modeller (t. ex. Bernmodellen) som utgår från att ökningen av koldioxidhalten helt beror på de antropogena utsläppen vilket kräver en uppehållstid i storleksordningen 100 år.
Vad jag anser om denna IPCC:s utvärdering av kunskapsläget framgår summariskt av mitt svar i #44.
Vi du veta mera om vari konflikten består, och varför det är en kärnfråga i klimatdebatten, så kan du t. ex. läsa kapitel 7–9 i http://www.falskt-alarm.se.
#41 Mats
Mats Almgren menar väl i sitt inlägg att den minskning som ses i bombprovskurvan delvis är en effekt av Suess-effekten dvs en utspädning pga tillförsel av C14-fri koldioxid.
”Minskningen av den naturliga nivån skulle ha fortsatt, om inte bombproven skett, och i allt högre takt allteftersom användningen av fossila bränslen ökade. Exakt hur den minskar är inte lätt att avgöra.”
”Enligt min grova uppskattning borde naturliga nivån ha minskat med 25-45% på de 50 år som förflutit sedan 1960. ”
Under tiden för bombprovskurvan så har koldioxidhalten i atmosfären ökat från ca 320 ppm till 390 ppm dvs +20%. Hur stor del av den ökningen är från fosilt koldioxid? Allt? Den del som är ett resultat av ökad utgasning från haven är inte fri från C14. Hur påverkar det den naturliga nivån?
Johan M #51
Mats Almgren förmår inte skilja mellan mängden C14 i atmosfären (opåverkad av fossila utsläpp) och isotopsammansättningen av luftens koldioxid (påverkad av Suesseffekten). Jag siktar på att få möjlighet att klargöra denna distinktion i ett kommande gästinlägg, förhoppningsvis inom 14 dagar.
Min kommentar #42 som svar på Mats fråga i #41 om Mats Almgrens blogginlägg på UI har fått ett svar av Mats Almgren i en kommentar till samma blogginlägg.
Där kommer han med en mycket märklig anmärkning om ekvation 1 i panelen på sidan 12 enligt länken till Sarmiento och Grubers bok som jag gav:
http://press.princeton.edu/chapters/s8223.pdf
”Den ekvationen är nog rätt tänkt, men formulerad på ett sätt som bäddar för missförstånd. ”
Alltså en insinuation om att Gösta Petterssons beräkningar är felaktiga.
Mats Almgren presenterar sedan en felaktig variant av ekvationen så som han tror att Gösta Pettersson har använt den. Detta är helt gripet ur luften. Han visar sedan en korrekt version av ekvationen som är den som han själv har använt.
För den som kan läsa innantill finns det inget rum för missförstånd. Det står klart och tydligt beskrivet i texten innan ekvation 1 att analysresultat för 14C presenteras som förhållandet 14C/12C i provet. Det står lika klart beskrivet hur spårämnesenheten Δ14C beräknas som en avvikelse från förhållandet 14C/12C i den förindustriella atmosfären som är standarden. Detta leder till ekvation 1 där dessa förhållanden betecknas med 14C_sample och 14C_standard.
Jag gissar att det som Mats Almgren gör i sin kommentar kan kallas för att skapa en halmgubbe.
Christopher e “38,
I teorin antar man att det förindustriellt var en dynamisk jämvikt mellan atmosfär, havets ytskikt och djuphavet.
För 12C ger detta en viss fördelning mellan atmosfär, havets ytskikt och djuphavet.
För 14C blir denna jämviktsfördelning approximativt densamma som för 12C. Men det blir vissa skillnader. Havets ytskikt kommer att innehålla endast 95% av den mängd som motsvarar om fördelningen var lika med den för 12C. Detta beror på den så kallade isotopeffekten som något förändrar hastighetskonstanterna för överföring mellan luft och hav och mellan hav och luft. Men det är fortfarande så att det förindustriella tillståndet antas vara ett dynamiskt jämviktstillstånd.
Detsamma gäller 14C i djuphavet. Där förskjuts den dynamiska jämvikten av ytterligare en faktor som inte påverkar 12C nämligen att 14C sönderfaller radioaktivt. Uppehållstiden i djuphavet är så lång så att denna sönderfallsreaktion också påverkar fördelningen så att mängden 14C sjunker till omkring 85% av vad som motsvarar samma fördelning som för 12C.
Dessa isotopeffekter är så små att man kan bortse från dem i de resonemang vi har här.
Tillskottet av 14C på grund av bombproven var ett nettotillskott. Upptaget av detta nettotillskott skedde på mycket nära samma sätt som om nettotillskottet i stället hade bestått av 12C.
I figur 1 i Joos med flera (1993) ser vi både Göstas blåa kurva som ger nettoupptaget av en stor mängd 12C och en bombkurva som ger nettoupptaget av ett mycket litet nettotillskott:
http://www.climate.unibe.ch/~joos/papers/joos96telb.pdf
Att kurvorna skiljer sig åt beror på att tillskottet har så olika storlek. Vid ett stort tillskott påverkas kolkemin i havet så att upptaget går saktare. Vid ett mycket litet tillskott går upptaget så snabbt det kan genom att kolkemin nästan inte påverkas. Men båda kurvorna uppvisar den form som beror på att modellen är flerfasig med särskilda delar för atmosfär, havets ytskikt och djuphav.
Det är att den verkliga bombkurvan inte visar denna flerfasiga form och dessutom visar ett betydligt snabbare avklingningsförlopp än den som modelleras enligt Bern som är den stora skillnaden.
#54 Pehr Björnbom
”Vid ett stort tillskott påverkas kolkemin i havet så att upptaget går saktare.”
Vad är det som orsakar detta, är det en en brist på kalciumjoner?
Har vi sett att upptaget går långsammare under bombkurvans tid? Har hastigheten på upptaget förändrats under 1900-talet och om så, visar det sig i bombprovskurvan?
Gösta #45,
Tyvärr måste jag konstatera att logiska argument inte biter på dig och Pehr i denna fråga. Vi har nu hamnat i den absurda situationen att UI argumenterar mer seriöst än TCS. Tragiskt! Och detta strax efter att det blivit klarlagt att vi skeptiker haft rätt hela tiden.
För övrigt ansluter jag mig till 100% till Nir Shavivs kommentarer om IPCC. Vetenskapen säger numera (även peer-review) att klimatkänsligheten är lägre än 2, det framgår tydligt även av IPCCs rapport, trots att dom gör allt för att snacka bort hårda fakta.
#52#54 Vore det inte trevligt med en genomgång tillsammans med kritikerna på UI ?
Eller är det en akademisk strid som pågår?
Lasse #57 Det är en bloggstrid, ingen akademisk strid. Akademikerna här vägrar ju konsekvent att ens försöka skriva ihop och publicera en vetenskaplig artikel i ämnet. De finner det uppenbarligen bekvämare att slippa konfrontera experter på kolcykeln.
Mats Almgrens blogginlägg på UI har korrigerats och där han hade skrivit halten 14C står det nu förhållandet 14C/12C. Han har ursäktat sig för att han uttryckte sig slarvigt. Med den nya skrivningen har jag lättare att acceptera vad han skriver.
Men fortfarande gör Mats antaganden som inte har någon grund. Han skriver om att jag och Gösta har använt den korrekta ekvationen hela tiden. Men varför skulle jag ha använt denna ekvation när jag inte har gjort några sådana beräkningar för att räkna om en experimentellt bestämd bombkurva från den ena enheten till den andra. Vad har Mats fått detta ifrån?
Vad jag har gjort är att jag läst innantill och konstaterat att vad jag kan se från litteraturen och av vad han själv skrivit är att Gösta Pettersson har använt korrekt beräkningsgång för att räkna om bombkurvan från den ena enheten till den andra. En rimlighetsbedömning säger också att en professor i biokemi (Gösta) borde vara minst lika insatt i detta som en professor i fysikalisk kemi (Mats).
Mats antar tydligen att jag har något slags nära samarbete med Gösta men så är inte fallet. Jag är mycket lite bekant med Mats Almgren, vi har haft en del emailkontakt och är bekantas bekanta genom Peter Stilbs, men jag är trots det mer bekant med Mats än med Gösta Pettersson (som jag visserligen också har haft emailkontakt med). Detta är en sak som jag menar visar att Mats gör ogrundade antaganden.
Gösta Pettersson kommer enligt egen utsago att kommentera de här frågorna om bombkurvan i ett blogginlägg om cirka fjorton dagar. Men, efter att Mats nu konstaterat att Gösta använt korrekt omräkning av bombkurvan, har jag en åsikt om vad kvarvarande meningsskiljaktigheter mellan Mats Almgren och Gösta Pettersson om bombkurvan består av baserad på hur den här diskussionen har utvecklat sig. Jag kan naturligtvis ha fel, vilket i så fall kommer att framgå, men jag ger ändå min åsikt här.
Mats Almgren menar att överskottet i mängden 14C som fanns år 1963 då bombkurvan hade sin topp inte har tagits upp av havet till mer än 60% och att det alltså finns 40% kvar från bombproven i atmosfären. Så tolkar jag hans tidigare blogginlägg.
Gösta Pettersson har i stället sett det som okänt hur mycket som tagits upp, dvs. hur mycket av 14C som är kvar efter bombproven. Han har anpassat bombkurvan mot en exponentialfunktion och har i samband med denna anpassning kunnat beräkna hur stor andel som finns kvar. Han plottar sedan resultaten i ett diagram med y-axel från 0 till 100%, varvid 0 motsvarar den mängd 14C som exponentialkurvan asymptotiskt närmar sig.
Min reflektion är att Gösta Pettersson har prövat en hypotes att bombkurvan följer ett enfasigt exponentiellt förlopp, motsvarande att havet kan representeras av en enda box, och att detta stämmer med observationerna. Det som finns kvar av oklarhet är att mängden 14C före bombproven inte stämmer med litteraturen. Men hur säkra är dessa siffror egentligen?
När Gösta Pettersson sedan enligt sitt paper 3 prövar hypotesen att koldioxidens absorbtion i havet kan representeras med en enboxmodell för havet om hastighetskonstantens för utgasningen temperaturberoende följer Arrhenius ekvation så får han ånyo en utmärkt överensstämmelse med observationerna. I detta senare fall har jag själv reproducerat hans resultat så jag kan garantera ätt det är på detta sätt.
Jag ser en stor potential i vad Gösta Pettersson här har åstadkommit där hans hypotesprövningar stämmer på alla ovannämnda punkter utom en. Man kan inte bara vifta bort dessa resultat utan att förklara hur de kan uppkomma.
Johan M #55,
När den antropogent utsläppta koldioxiden löser sig i havet så bildas det vätejoner genom kemiska reaktioner. Enligt teorin kommer den ökade vätejonhalten att försvåra upplösningen av koldioxid i havets ytskikt så att upplösningen går mycket långsammare. Det är därför som den antropogena koldioxiden stannar kvar i atmosfären så länge.
Gösta Pettersson har använt enkla matematiska modeller som utgår ifrån att koldioxiden inte löses upp långsammare av denna orsak. Det märkliga är att hans modeller visar sig stämma så bra med observationerna.
Gösta Pettersson har alltså genom sitt forskningsarbete testat hypotesen bildning av vätejoner gör att koldioxiden absorberas långsammare. Om hypotesen skulle vara riktig borde hans matematiska modeller inte kunna överensstämma med observerade data. Men det gör de och detta kan tyda på att hypotesen inte är giltig.
Det är detta som gör Gösta Petterssons resultat så märkligt. Den sedan länge förmodat riktiga hypotesen, att bildning av vätejoner när koldioxiden löses i havsvatten gör att absorptionen går mycket långsammare, motsägs markant av hans resultat.
Pehr Björnbom #59
”Gösta Pettersson har i stället sett det som okänt hur mycket som tagits upp, …”
”Det som finns kvar av oklarhet är att mängden 14C före bombproven inte stämmer med litteraturen.”
Tack Pehr för ditt försvar av mina kurvanalyser. Men dina uttalanden ovan kräver kanske ett förtydligande:
Jag har inte sett någonting som okänt, utan endast redovisat den okorrigerade bombprovskurvan så som Nydal & Lövsedt själva presenterat sina resultat. Det är norrmännen själva som har definierat vad de anser vara startnivån före bombproven och som har angett sina mätvärden som ett överskott i förhållande till denna nivå. Jag utgår från att de har full koll på sina startvärden och betraktar dem som överensstämmande med litteraturen (vilken i detta fall skrivits av dem själva).
Det enda jag har gjort är att visa att deras kurva bäst beskrivs som monoexponentiell med ett slutvärde nära noll, dvs. nära det av norrmännen definierade startvärdet före bombproven.
#60 Pehr Björnbom
Vari ligger begränsningen? Om det enbart hade varit en reaktion C02 + H20 HC03- + H+ så hade en en ökning av C02 gett en direkt proportionell överföring till HC03- + H+ . Att havet skulle bli mindre basiskt kommer som ett brev på posten men är ingenting som skulle förhindra upptaget av koldioxid. Överföringen är direkt proportionell till koldioxidkoncentrationen.
Revelle-effekten grundar sig väl i hur sen Ca2+ joner står i jämvikt med HC03- och hur den jämvikten påverkar flödet Ca2+ HCO3- CaCO3(s) + H+
Vi har då:
C02 + Ca2+ + H20 Ca2+ HC03- + H+ CaCO3(s) + 2H+
Så länge vi har ett överskott på Ca2+ joner så kan vi förskjuta reaktionen åt höger men om dess koncentration minkar så ligger jämvikten till vänster.
Har jag förstått rätt?
Trenden på temperatursänkningen som Miklip prognostiserar(?) är rejäl: 1-1.5K på ca 7 år.
Får de rätt är detta spiken i kistan för CAGW, och antagligen för AGW också.
Inlägget kom i fel tråd. Ta gärna bort inlägg#63 här
Tack på förhand
#62 Johan M
hmm, alla pilar borta … sätt in dubbelriktade pilar på väl valda ställen:
C02 + H20 —– HC03- + H+
Ca2+ HCO3- —– CaCO3(s) + H+
C02 + Ca2+ + H20 —– Ca2+ HC03- + H+ ——- CaCO3(s) + 2H+
#61 Gösta Pettersson
”… utan endast redovisat den okorrigerade bombprovskurvan så som Nydal & Lövsedt själva presenterat sina resultat.”
Om bomprovskurvan är okorrigerad ,och visar förhöjning av 14C koncentrationen givet ett standardvärde från 1950, så är det väl högst relevant hur en korrigerad kurva ser ut och hur denna korrigering görs?
Johan M #66
”högst relevant hur en korrigerad kurva ser ut och hur denna korrigering görs”
Ja, det är rätt, men lösningen på det problemet är Pehr och jag redan överens om.
Det jag tyckte behövde förtydligas var att jag inte på något stadium av min analys infört några egna antaganden om start- eller slutnivåer.
Johan M #62,
Kemin för Revelleeffekten är rätt komplicerad. Jag hade ett blogginlägg om den där jag försökt förklara en del av denna:
https://www.klimatupplysningen.se/2013/08/30/revellefaktorn-lika-viktig-klimatkansligheten/#.Ul7Swylvlq0
Revelleeffekten beror på att koldioxidens löslighet i havsvatten minskar när vätejonhalten ökar, dvs. när pH minskar, samtidigt som koldioxiden själv är en svag syra som bildar vätejoner när den löses upp. Om man har något i havsvattnet som reagerar med vätejoner, till exempel CaCO3, så minskar Revelleeffekten betydligt och mycket mer koldioxid kan lösas upp.
Den kemivetenskapliga teorin bakom detta beskrivs i Bolin och Eriksson (1959) som jag referare till i blogginlägget. Länk till artikeln:
http://nsdl.org/sites/classic_articles/Article8.htm
Mats Almgren har på UI gjort en slutkommentar om bombkurvan enligt Gösta Pettersson.
Han påstår nu att han inte insinuerat men hela tiden velat påstå att Gösta Petterssons omräkning av Δ14C-data är felaktig. OK, då har jag tydligen missuppfattat hans sätt att uttrycka sig och tackar för att han nu talar ur skägget.
Mats Almgren påstår alltså att de punkter som Gösta Pettersson har beräknat och som finns i det översta diagrammet ovan är felaktigt beräknade från de Δ14C-data som han utgått ifrån (se tidigare gästinlägg av Gösta Pettersson).
Ett sådant påstående kräver bevis men något sådant ger inte Mats Almgren. Han hänvisar bara till diagram från litteraturen men dessa diagram är inte organiserade i en sådan skala som Gösta Pettersson har använt, alltså övergång mellan två mängdnivåer, den ena toppnivån som är 100% och den andra asymptoten som är noll.
Upp till bevis, Mats Almgren! Hur skall enligt Dig ett korrekt diagram som går mellan dessa två mängdnivåer se ut och hur mycket skiljer det sig, om något, från Gösta Petterssons diagram?
En intressant sak i debatten med Mats Almgren är att han säger att det fortfarande finns 40% kvar av 14C efter bombproven. Det innebär i så fall att bombkurvan överensstämmer med Bernmodellen enligt den blå kurvan i översta diagrammet.
Pehr, jag tyckte jag skrev helt klart att GP begått en blunder. Men det kanske fastnade i halmskägget!
Däremot har jag inte presenterat en klar formel för hur ändringen av C14 koncentrationen kan beräknas ur ∆C14-värdena. Så jag gör det nu.
∆C14 = (n14/n12)/(n14s/n12s) -1
Denna formel var vi överens om (isotopkorrektionen satt = 1). Kvoten n14s/n12s är för standardens, som vi kan välja till värdena just före bombproven; ∆C14 = 0 gäller då. För att beräkna n14 från de rapporterade ∆C14-värdena skriver vi
n14 = (∆C14 + 1)·(n14s/n12s)·n12
Den relativa ändringen av n14 i förhållande till nivån före proven fås då enkelt:
∆n14 = (n14/n14s) -1 = (∆C14 + 1)·n12/n12s – 1
Här fås n12/n12s ur Keelingkurvan. Enligt Gösta ger hans ”korrektion” ett resultat som skiljer sig obetydligt från ∆C14. Men det gör inte ∆n14 enligt denna formel. När ∆C14 nu börjar bli liten så är termen
n12/n12s – 1 betydande.
Är du nöjd nu?
#71 Mats Almgren
En fråga bara om jag har förstått vad parametrarna står för och deras värden:
∆C14 : överskottet enligt de mätningar vi har relativt standardvärdet, för år 2000 ca 5% ?
n12/n12s : ökningen av koldioxidnivån från standardvärdet, för år 2000 ca 1.2 ?
∆n14 : det justerade värdet för överskottet, för år 2000 med antagande ovan 26%
#72 Johan M
Det är nog rätt uppfattat.
Mats #71,
Nej, Mats, jag är inte nöjd. Det du anför är inte ett bevis för att Gösta Pettersson har räknat fel ens om han skulle ha gjort det.
Gösta har plottat de omräknade värdena på en skala från noll till 100%. Nollnivån uppfattar jag som att den mängd 14C som exponentialfunktionens asymptot bestämmer. Nivån 100% uppfattar jag som den mängd 14C som motsvarar bombkurvans topp.
Göstas kurva motsvarar kurvan för troposfären från toppvärdet och framåt i tiden enligt figur 2b i följande artikel av Levin och Hesshaimer (2000):
https://journals.uair.arizona.edu/index.php/radiocarbon/article/view/3855/3280
Tänk Dig att Du lägger in en y-axel i detta diagram som är graderad med 100 vid troposfärkurvans toppvärde och med noll vid det värde som motsvarar den asymptot som troposfärkurvan går mot. Då får man diagram där troposfärkurvan efter toppen ser ut på samma sätt som Göstas diagram.
Det Du alltså måste visa för att bevisa att Gösta har räknat fel är att visa att punkterna med de omräknade värdena i det översta diagrammet i Peters blogginlägg ovan ligger fel. Men även de korrekt beräknade punkterna skall ju definitionsmässigt gå från noll till 100% där nollnivån definieras av den anpassade exponentialfunktionens asymptot. Det är så jag hela tiden har tolkat detta diagram och en sådan tolkning stämmer ju också perfekt med hur diagrammet ser ut.
Så för att bevisa att Gösta har räknat fel måste Du faktiskt genomföra beräkningar på åtminstone några punkter.
Pehr #74: Jag instämmer helt i ditt resonemag. Var det för övrigt inte Dirac eller Feynman som myntade uttrycket ”shut up and calculate”?
Nu har du ju själv talat om att det är Gösta som gjort de här beräkningarna, och inte alls du. Och Gösta beskriver dem själv i #61som följer:
”Jag har inte sett någonting som okänt, utan endast redovisat den okorrigerade bombprovskurvan så som Nydal & Lövsedt själva presenterat sina resultat. Det är norrmännen själva som har definierat vad de anser vara startnivån före bombproven och som har angett sina mätvärden som ett överskott i förhållande till denna nivå. Jag utgår från att de har full koll på sina startvärden och betraktar dem som överensstämmande med litteraturen (vilken i detta fall skrivits av dem själva).”
Det stämmer med vad jag har gjort. Och att få skalan att gå från 100 till 0 är ju inte särskilt svårt. Det ändrar inget i sak.
Att ha en nollnivå som ligger långt över nivån före bombproven kräver en fysikalisk förklaring.
Nu kommer jag inte att öda mer tid på detta.
Mats #76,
Med stöd från Michael #75 så tycker jag att när du kommer med ett sådant påstående så borde du bevisa det med en egen beräkning, Det är ju inte särskilt svårt att beräkna några punkter på korrekt sätt i Göstas diagram. Rent intuitivt tycker jag inte det ser ut att vara några stora skillnader mellan en korrekt beräknad kurva och en som är felaktigt beräknad enligt det fel du påstår Gösta har gjort.
Jag håller naturligtvis med dig att det kräver en fysikalisk förklaring varför nollnivån ligger på ett högre värde än 1950. Men denna frågeställning är ju ingenting nytt, som sagt i min förra kommentar så framgår den av Levin och Hesshaimer (2000). Det var ju också därför jag skrev:
”Gösta Pettersson har i stället sett det som okänt hur mycket som tagits upp, …”
”Det som finns kvar av oklarhet är att mängden 14C före bombproven inte stämmer med litteraturen.”
Du citerar från Göstas svar till mig på denna punkt. Men jag uppfattade hans svar på ett annat sätt än dig, nämligen att han talade om den okorrigerade kurvan med Δ14C, där värdena före och efter onekligen är kända.
Fysikaliska förklaringar är möjliga. Man kan fråga sig vad osäkerheten är i mängden 14C när man före Keelings mätningar bara hade Δ14C men inte mätningar av koldioxidhalten i atmosfären. En annan fråga är om man inte borde ta hänsyn till temperaturens inverkan på liknande sätt som Gösta gjort när han modellerat Keelingkurvan med en modell med en box för atmosfären och en box för havet. En förklaring skulle alltså kunna vara att ökad temperatur minskar flödet av 14C mellan atmosfären och havet. En tredje möjlighet är den jag tidigare bloggat om att upplöst antropogen koldioxid genom Revelleeffekten minskar flödet av 14C mellan atmosfären och havet.
[…] Almgren har beskrivit det fel han tror att Gösta Pettersson har gjort i en kommentar i blogginlägget av Peter Stilbs Bombprovskurvan, Bernmodellen och kemisk kinetik – några […]