Resultatet av mätningar med satellit blev för september + 0,54 grader högre än genomsnittet 1981 – 2010 enligt UAH
| YEAR | MO | GLOBE | NHEM. | SHEM. | TROPICS |
| 2016 | 1 | +0.55 | +0.72 | +0.38 | +0.85 |
| 2016 | 2 | +0.85 | +1.18 | +0.53 | +1.00 |
| 2016 | 3 | +0.76 | +0.98 | +0.54 | +1.10 |
| 2016 | 4 | +0.72 | +0.85 | +0.58 | +0.93 |
| 2016 | 5 | +0.53 | +0.61 | +0.44 | +0.70 |
| 2016 | 6 | +0.33 | +0.48 | +0.17 | +0.37 |
| 2016 | 7 | +0.37 | +0.44 | +0.30 | +0.47 |
| 2016 | 8 | +0.43 | +0.54 | +0.32 | +0.49 |
| 2016 | 9 | +0.45 | +0.51 | +0.39 | +0.37 |
| 2016 | 10 | +0.42 | +0.43 | +0.42 | +0.47 |
| 2016 | 11 | +0.46 | +0.43 | +0.49 | +0.38 |
| 2016 | 12 | +0.26 | +0.26 | +0.27 | +0.24 |
| 2017 | 1 | +0.32 | +0.31 | +0.34 | +0.10 |
| 2017 | 2 | +0.38 | +0.57 | +0.19 | +0.07 |
| 2017 | 3 | +0.22 | +0.36 | +0.09 | +0.05 |
| 2017 | 4 | +0.27 | +0.28 | +0.26 | +0.21 |
| 2017 | 5 | +0.44 | +0.39 | +0.49 | +0.41 |
| 2017 | 6 | +0.21 | +0.33 | +0.10 | +0.39 |
| 2017 | 7 | +0.29 | +0.30 | +0.27 | +0.51 |
| 2017 | 8 | +0.41 | +0.40 | +0.41 | +0.46 |
| 2017 | 9 | +0.54 | +0.51 | +0.57 | +0.53 |
.

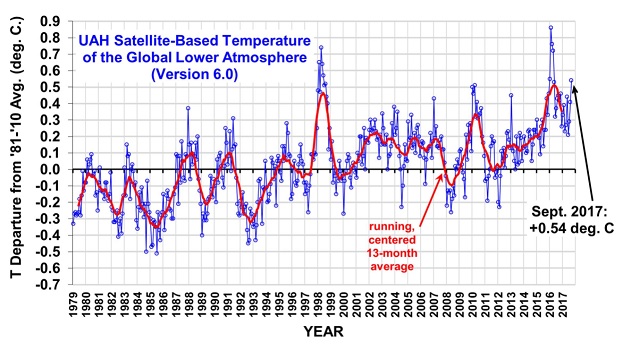






Det var förvånande, det är ju varmaste september-månaden någonsin i indexet, 0,09 C mer än 2016 och 0,10 mer än 1998.
2017 har goda chanser att bli tredje varmaste året (och peta ner 2010 till fjärdeplatsen). Då ska man tänka på att 2010 var ett medelstarkt el Nino-år medan 2017 inleddes med svag la Nina..
Temperaturerna i UAH har dock skruvats upp en aning sedan de nyligen introducerade den ickedrivande Metop-B-satelliten, med data från mitten av 2013 och framåt..
Ganska fantastiskt att man kan mäta den globala temperaturen men hundradels noggrannhet, jag menar ”0,09 C mer än 2016 och 0,10 mer än 1998”. Undra om Klotet i P1, SvD eller DN gör detta til en uppseendeväckande nyhet? Bara för att skrämma upp folk ytterligare och öka på klimatångesten hos de redan ångestfyllda.
#2 Greger ”Ganska fantastiskt att man kan mäta den globala temperaturen men hundradels noggrannhet”
Nej, man kan inte mäta den globala temperaturen ned en noggrannhet på 0.01°C, (den är ca 15 °C) , men förändringen i temperatur kan mätas ätt noggrant.
#1 Olle R
”Temperaturerna i UAH har dock skruvats upp en aning sedan de nyligen introducerade den ickedrivande Metop-B-satelliten, med data från mitten av 2013 och framåt..”
Det förklarar en del.
Någon som vet hur en icke justerad temperaturserie ser ut?
#2 Nu är iofs UAH bara ett temperaturindex, inte temperaturen själv.
Det är Spencer&Christy som bestämmer reglerna för indexet, ganska subjektivt emellanåt:
Vilka satelliter som får vara med, vilka som är ”rätt” och ”fel”, hur de ska justeras, etc..
När dessa regler väl är bestämda menar Spencer att konfidensintervallet är +/- 0,10 grader, så ja i strikt mening kanske inte månadens värde är signifikant varmare än 1998, men kan lika gärna vara 0,20 grader varmare.
Om man tar hänsyn till den strukturella osäkerheten (alla valmöjligheter som finns) så är osäkerheten i vad den verkliga temperaturen är ca 5 ggr större, men eftersom S&C plockat sig fram väldigt lågt från detta smörgåsbord, så sträcker sig nog osäkerhetsintervallet bara uppåt från deras angivna temperatur.
Sen kan man ju också undra vad TLT egentligen är för slags temperatur och vad den representerar. Idealiskt ska den ju härröra ur mikrovågsstrålning i vissa frekvenser, baserat på en viktningskurva över breda atmosfärslager som bygger på strålningsteori, och en atmosfär med fixa tryck/höjd/temperaturförhållanden kallad US Standard atmosphere 1976.
En egenhet med dessa temperaturindex, såsom de räknas, är att tunn luft högt upp betyder lika mycket som luft med hög densitet nära ytan, dvs de avspeglar inte energiinnehållet i luftpelaren. Detta är en av förklaringarna till att satellitindexen reagerar starkare på el Nino än ytindexen, för under el Nino stiger temperaturen mer högt upp i troposfären (men det är tunn varm luft däruppe, inte så mycket energi)
Torbjörn #4 ”Någon som vet hur en icke justerad temperaturserie ser ut?”
Det är omöjligt att göra en sådan för dessa satelliter. Man måste justera för banförändringar, att man byter satellit, att satelliterna mäter någon sorts temperaturindex för hela atmosfären osv. Det är bara det att ansvariga här har bestämt att dessa justeringar är bra ( i alla fall om de görs av Spencer och inte av Mears) medan justeringar av markdata kallas för ”manipulering” och är bevis på fusk.
Olle R m.fl.
Notera att satellitmätningarna började 1979 som var ett ovanligt kallt år. Så att vi nyligen har haft de ”varmaste åren någonsin” (sedan satellitmätningarna började alltså) betyder därför inte så mycket.
#4 Måste förtydliga, temperaturerna ökar en smula för att Spencer & Christys diurnal drift korrigering ”vattnas ur” med en satellit som inte driver och inte behöver justeras.
Av någon anledning har UAH valt bort den Ickedrivande satelliten Metop-A som hade kunnat ge data utan justeringsbehov från hösten 2006. Undrar hur temperaturerna hade blivit då?
Kanske UAH 5.6 kan indikera detta, eftersom den bygger enbart på icke-drivande AMSU-satelliter och satelliter som driver minimalt, och därför inte behöver justeras..
Beträffande ENSO så förutspåddes det en ny El Nino under våren. Istället så har det varit neutralt läge sedan försommaren. Nu verkar det som om prognosmakarna förutspår en La Nina i vinter, med effekter (dvs en nedkylning) för oss här uppe till våren. Men det är förstås även andra faktorer som också påverkar hur våren blir i Skandinavien.
http://www.cpc.ncep.noaa.gov/products/analysis_monitoring/enso_advisory/ensodisc.shtml
#6 Thomas P
Det behöver inte vara en satellitmätning.
Det finns ju bojar, ballonger och fasta mätpunkter.
Skulle vara intressant att se en serie utan justeringar
#8 Olle R
Men det förklarar varför UAH index stiger snabbare de sista fyra åren
Mäter satelliterna norra halvklotet eller hela klotet ?
#3 Kan du förklara lite närmare, hur det fungerar att man kan inte kan mäta den globala medeltemperaturen särskilt noga, men däremot temperaturen rätt noggrant? Jag tycker det låter magiskt.
#12 Lasse J: ”#3 Kan du förklara lite närmare, hur det fungerar att man kan inte kan mäta den globala medeltemperaturen särskilt noga, men däremot temperaturen rätt noggrant? Jag tycker det låter magiskt.”
Det var inte det jag skrev:. Det står ”Nej, man kan inte mäta den globala temperaturen ned en noggrannhet på 0.01°C, (den är ca 15 °C) , men förändringen i temperatur kan mätas rätt noggrant.” Märk ordet ”förändringen i temperatur” i bisatsen. Då håller du kanske med. Om du inte håller med kan du se på den här. Jag refererar inte ofta till WattsUpWithThat”, men i det här fallet har Bob Tisdale ändå hittat et korn: https://wattsupwiththat.com/2014/01/26/why-arent-global-surface-temperature-data-produced-in-absolute-form/
Hösa #111 Satelliterna mäter allt utom områdena kring polerna. Hur väl man sen kan räkna om den mikrovågsstrålning de mäter till temperatur är en annan sak.
#12 Lasse J
Tänk en termometer utanför fönstret med alla strecken kvar men där siffrorna har blivit utsuddade. Du kan mäta små förändringar men vet egentligen inte (och bryr dig inte) om det är 12 eller 14 grader utomhus.
Innan man förfasas över dessa rekord kan man ju identifiera var värmen finns!
”Compared to seasonal norms, the warmest place on Earth in September was the Norwegian archipelago of Svalbard in the Arctic Ocean. Temperatures there averaged 4.64 C (about 8.35 degrees Fahrenheit) warmer than seasonal norms.”
https://wattsupwiththat.com/2017/10/02/global-temperature-report-september-2017/
Från DMI kan man ana att denna anomali inte påverkar hela Arktis:
http://ocean.dmi.dk/arctic/meant80n.php
Jag hade förväntat mig finna orkanernas värme på anomalikartan-men den försvann väl med orkanerna.
#16 forts
Norrmännen diskuterar denna värme: https://www.nrk.no/nordland/derfor-er-det-grunn-til-a-vaere-bekymret-over-finvaeret-i-nord-1.13713981
Lita av ormtjusaren i Kivik över det hela, Farligt men inte här!
Tack för svaret.När jag tittade på grafens topp står det Södra o Norra +tropics,men södra består väl mest av vatten,blir inte det svårt att mäta,eller mäter man bara Sydamerika,Australien och södra Afrika,s landområden.Och hur räknar man ut ett medelvärde på ett klot?
Erik Lindeberg 13
Tack för länken. Man fick verkligen mycket att tänka på betr. relationen anomali/ absolut temperatur.
Min reflexion är att anomalier förvränger perspektivet både i tid samt omfång betr. global temperatur.
Alltså närmast propaganda.
Rita istället upp absolut temperatur och anomali i samma skala och förstå relationen. Säsongsvariationen betr. globala temp. rör sig om + – 2,5 C men anomalier om tiondelar.
Jovisst har temp ökat i ett hundraårsperspektiv (trädgränsen) men perspektivet borde vara 500-1000 år
För att få ytterligare perspektiv kan man rita in temperaturer resp anomalier från norra resp södra halvklotet årsvis från 1979 med samma skala.
NH: 14,5 +- 7,1 C sommar/vinter. Anomali-range : 1,6 C
SH: 13,2 +- 3,3 C sommar/vinter Anomali-range : 1,3 C
Hösa #18 De här satelliterna mäter termisk utstrålning från atmosfären så om det är mark eller hav under spelar i teorin ingen roll (i praktiken får man en del strålning från marken också som komplicerar tolkningen) . Det är bara runt polerna man missar för att satelliternas banor inte når upp dit.
Varför skulle det vara svårare att räkna ut medelvärde för att jorden är ett klot? Man delar in jorden i små rutor, ser hur temperaturen ändrats i var och en av dem och tar ett medelvärde för att få den genomsnittliga globala temperaturanomalin.
I stället för de planerade 1500 elektriska mellanklassbilar byggde Tesla HELA 260 i tredje kvartalet. Investerare reagerar besviket, aktiekursen sjunker.
Fram till året slut borde månadsproduktionen höjas till 5000. Osannolikt, säger finansexperter.
Musk lär vara på rundresa i Europa för att samla subventioner. När tar Löfven emot?
AHA, därför rubrikerna om bosättningar på månen och raketer som tar turister som vi fick veta om i våra fina grönspolade medier.
Symtomatiskt, att en garagemanufaktur som Tesla får sådana rubriker hos oss!
Thomas P #20
”Varför skulle det vara svårare att räkna ut medelvärde för att jorden är ett klot? Man delar in jorden i små rutor, ser hur temperaturen ändrats i var och en av dem och tar ett medelvärde för att få den genomsnittliga globala temperaturanomalin.”
Du får det att låta lätt. Så här kan och görs det, men dina små rutor är inte nödvändigtvis så små. Om rutan är 1000 x 1000km så betyder det att Kiruna kan få en anomali som hör hemma i Uppsala eller tvärtom. Det blir liksom inte rätt.
I somras t.ex. gjorde jetströmmen en skarp gräns i Europa där södra halvan var extra varm och norden extra kall. Om du då drar din ruta så att den räknar med södra sidans värme till norra sidan, blir det ett klart fel. Redan det här gör tionde och hundradedelsgrader löjliga. Det blir endast en matematisk konstruktion utan förankring i verkligheten.
Inom naturvetenskapen, till skillnad från diverse andra discipliner som inom sociologi och humaniora, är man ibland tvungen att acceptera resultat som man inte gillar även om de inte stämmer överens med ens förutfattade meningar. När nu även de satellitbaserade observationerna visar en otvetydig långsiktig uppvärmning blir det givetvis allt svårare att hålla fast vid motsatsen.
Detta innebär förvisso inte att man måste ställa sig bakom den svenska ”klimatpolitiken”.
Lennart Bengtsson [23]; Jag skulle vilja säga att satelliterna visar på det faktiska temperaturförhållandet. Ingen värme kan smita ut utan att satelliterna ”ser” vad som händer. Temperaturen blir som den blir, men dess orsak är det kontroversiella. En annan sak som kan var intressant att spekulera kring är följande. Det är ju ett faktum att vår polnära jetström gör avstickare söderut under vinterhalvåret, men att denna migrering söderut, även blir vanligare under andra årstider. Gränsen mellan kall och varm luft flyttar alltså söderut. Detta skeende kan väl knappast vara konsekvensfritt? Luftvolymen mellan den polnära och subtropiska jetströmmen krymper. Om samma mängd värme breder ut sig mot norr från ekvatorområdet (subtropiska), blir det då inte varmare inom denna krympta volym?
Guy #22 Varför slår du inte upp vad man har för spatiell upplösning på dessa satelliter…
Thomas P # 25
Ber så mycket om ursäkt. Visste inte att din kommentar gällde enbart satelliter. En massa temperaturer har extrapolerats i rutor/cirklar om 1000 – 1200km. Kanske det inte görs längre om dom har insett vilket vansinne det var. För att inte tala om hur fel resultatet kunde bli.
Hoppfullt när modellmakarna lär sej 🙂
En fundering.
Resonemanget kring behovet av en global medeltemperatur som ett mått på en ev. global uppvärmning utgår såvitt jag förstår ifrån strålningsbalans och hur denna förändras över tid.
Men utstrålningen är enligt Stefan-Boltzmanns lag inte proportionerlig mot T utan mot T^4.
Är det inte därmed egentligen meningslöst att beräkna medeltemperaturen (T) och tro att detta är en bra indikation på strålningsbalansen?
Det rimliga vore väl att beräkna medel-T^4 istället, och helst över ett helt dygn?
Exempel. Anta två områden på jorden med exakt samma area. Område A har temperaturen -30 °C (243 K) och område B +30 °C (303 K). Medel-T är 0 °C (273 K). Sammanlagda utstrålningen för A+B blir då proportionerlig mot 243^4 + 303^4 = 11 915 676 882.
Vad händer nu om A blir 1 grad kallare och B blir 1 grad varmare? Jo, Medel-T för A+B blir fortfarande 0 °C (273 K) men den sammanlagda utstrålningen blir istället proportionerlig mot 242^4 + 304^4 = 11 970 459 152, dvs. utstrålningen har ökat med ca 0,46 %.
Man kan givetvis också ta fram exempel där medeltemperaturen ändras men utstrålningen är konstant.
Någon annan som funderat i liknande banor?
#18 Jensen: ”Rita istället upp absolut temperatur och anomali i samma skala och förstå relationen. ”
Då har du inte förstått länken jag skickade. Man lär ingenting om man drunknar signalen i brus, altitudvaritioner, årstidsvariation osv. Den absoluta global temperaturen är 15 °C ± 0.5 °C.! Kanske den här länken beskriver problemet med absolut temperatur bättre: http://www.realclimate.org/index.php/archives/2017/08/observations-reanalyses-and-the-elusive-absolute-global-mean-temperature/
Vidare: ”Jovisst har temp ökat i ett hundraårsperspektiv (trädgränsen) men perspektivet borde vara 500-1000 år”.
Det beror nog på vilket syfte din analys har. 500 – 1000 år tidsperspektiv är bra för att kartlägga baslinjen och naturliga långtidsvariationer, men skal vi analysera den mänskliga påverkan och korttidsvariationer måste vi fokusera på ett kortare tidsperspektiv. Att kombinera båda i samma graf är svårt: https://drive.google.com/open?id=0B19Sr_Qmr4GJU2pDWUw2bTMwRGc , och ger mest långtidsvariationer och man missar kortidsvaritioner som till exempel ENSO-cykeln och stora vulkanutbrott . Det kan man få här: https://drive.google.com/open?id=0B19Sr_Qmr4GJX3BVTV9MdzN0ZHM
KM 27
Ligger i linje med att OLR bestämmes av jordens aktuella temperatur och inte av temp. anomalin, som sålunda inte styr jordens klimat. OLR är termostaten för jordens temperatur, där tidsskalan är hundratals år. ( t.ex. Lilla istiden.)
Innebär även att temp.oscillationen är range bound.
Enl. IPCC värmes jorden upp 3 C vid en fördubbling av CO2 dvs en forcing av 3,7 W/ m2. Problemet fö IPCC blir dock att jorden skulle förlora 7,5 W/m2. d.v.s. mer än dubbelt gentemot forcing-effekten.
Detta innebär även omöjligheten att jorden skulle snabbt värmas upp, när den redan är varm. Detta skulle kräva permanent ökning av energi från solen, vilket inte kommer att bli fallet.
Erik Lindeberg 28.
Tack för kommentaren.
Åsikter skall givetvis alltid vara fria, vilket uppskattas.
Du har säkerligen viktiga argument. Den nya länken gick dock utanför min fattningsförmåga, eller så hade jag inte tid eller koncentrationsförmåga att förstå riktigt.
Betr. syftet med mitt perspektiv i förhållande till ditt skiljer de sig givetvis åt.
Mitt är baserat på en genuin verklighet och inte minst att kunna sänka oron för tipping point.
Dina 2 sista länkar var ju intressanta, men för min del lite för auktoritetsbundna. Jag tänker på UHI och manipulationer.
Men tack.
jensen. #29
Tackar, intressant! Ska läsa på lite mer om OLR.
Har ytterligare en fundering kring mitt exempel. Visst är det väl också så att den totala termiska energin för A+B är oförändrad då A blir 1 grad kallare och B en grad varmare? (Temperatur är ju ett mått på den genomsnittliga kinetiska energin.)
Om det stämmer så har vi alltså två ”tillstånd” med samma medeltemperatur, samma totala termiska energi men olika nivåer på utstrålning/OLR.
Tänkte här göra en koppling mot Björns kommentar #24. Vad händer om ett område, som redan är varmt, t.ex. på grund av en jetströms ändrade bana blir ytterligare lite varmare? Jo, den totala utstrålningen ökar – även om det samtidigt uppstår en lika stor lokal temperatursänkning någon annanstans (i ett svalare område), så att den globala medeltemperaturen förblir oförändrad.
(Den ökade utstrålningen kommer förstås i nästa steg orsaka en avkylning.)
#30 KM
Mycket intressant observation, har aldrig reflekterat över det.
#27 Precis, korrekt sätt att räkna fram Jordens genomsnittliga utstrålning är att räkna ut utstrålningen vid alla punkter/tillfällen och sedan ta genomsnittet av det, istället för att ta genomsnittstemperaturen och räkna ut utstrålningen.
#30 ”(…) A blir 1 grad kallare och B en grad varmare (…)” Nu gör du ju det tankefel som du lyfte fram i 27. Den totala termiska energin är högre, genomsnittstemperaturen oförändrad och OLR högre.
Det är väl en aningen paradoxalt att marginellt högre temperatur, vilket satelliterna rimligen mäter som högre utstrålning, beror på lägre OLR vid TOA..?
Erik. #32
Jag tror inte att jag gör samma tankefel men tar tacksamt emot synpunkter.
Med termisk energi menar jag den sammanlagda kinetiska energin för gaspartiklarna i systemet.
Ytterligare ett tankeexperiment får illustrera:
Tänk två lika stora kärl, C och D, med olika temperaturer som är perfekt isolerade mot omvärlden: ingen strömning, ledning eller in- eller utstrålning så ingen energi avges eller tillförs. Energin i systemet är därmed konstant.
Förbind nu kärlen med varandra och temperaturen kommer p.g.a. termodynamikens lagar att jämnas ut mellan de båda kärlen. Den totala energin i systemet är dock fortfarande densamma.
I det ursprungliga tillståndet, med en temperaturdifferens mellan C och D, hade den totala utstrålningen (som vi valde att bortse ifrån) varit högre eftersom utstrålningen är proportionerlig mot T^4 och inte T.
KM #34 Skall du räkna med utstrålning och medel av T^4 så får du också tänka på att utstrålningen inte kommer från marknivå utan högre upp i atmosfären, så då får du räkna på temperaturerna där (och höjden varierar i sig med latitud m m) snarare än vid marknivån. På det stora hela är det enklare att bara ta medel av temperaturen vid marken. Det är trots allt här nere vi bor.
Thomas P. #35
Visst, det är såklart orealistiskt att tro att det går att få tag i temperaturdata i 3D i hela troposfären.
Men minimum vore väl att räkna medel-T^4 vid marknivå över hela 24-timmarscykler. Man kan ju sedan ta fjärderoten på detta och på så vis beräkna en sorts ”medeltemperatur”.
Detta borde ge en bättre indikation på strålningsbalansen än ett vanligt medelvärde.
KM #36 Du kan räkna hur du vill naturligtvis, men jag måste erkänna att jag har svårt att se poängen med att trassla till det. Tittar du vid markytan handlar det inte bara som strålning utan även om konvektion och latent värme, och de skalas inte som T^4. I praktiken blir det i alla fall inte någon större skillnad.
Thomas P. #37
Om det blir någon större skillnad eller inte vet vi ju inte, förrän någon provat att göra beräkningarna på aktuella temperaturdata. Ibland behöver man ta till lite krångligare metoder för att få ett mer korrekt resultat. Jämför t.ex. Newton och relativitetsteorin vid högre hastigheter.
#34 Premissen är väl att den nya genomsnittstemperaturen blir Tcd = (Tc + Td)/2 ? Och det kan väl knappast stämma.
Erik. #39
Lite naivt tror jag det kan stämma. Blanda 1 liter 20-gradigt vatten med 1 liter 30-gradit vatten så får du 2 liter 25-gradigt vatten, eller?
KM #38 Då får du allt definiera vad du menar med ”korrekt resultat”`. Vad tänker du dig för experiment som skall avgöra vilket sätt att ta medelvärde som är ”korrekt”?
Thomas P. #41
Intressant fråga. Om medeltemperaturen skulle visa sig bli mer stabil, även över kortare perioder, så kan det vara ett tecken på att det är ett bättre sätt att räkna.
CO2-halten stiger ju kontinuerligt i en jämn och fin kurva, så om man tror på koldioxidens stora inverkan på växthuseffekten->strålningsbalansen->temperaturen så är det väl inte orimligt att tänka sig att medeltemperaturen också borde göra det?
KM #42 jag har svårt att tänka mig att man skall få bort sådant som svängningarna av El Nino med ett sådant knep. det enda man i praktiken gör är ju att vikta upp jordens varmare områden i förhållande till de kalla.
Lite sent på bollen, men jag hittade en intressant bloggpost med en jämförelse mellan solinstrålning (ASR), utstrålning (OLR) och global medeltemperatur (UAH v6):
https://okulaer.wordpress.com/2016/01/07/uah-v6-vs-ceres-ebaf-toa/
I graferna ser man att de variationer i OLR som kommer från El Niño/La Niña är mindre än motsvarande variationer i den globala medeltemperaturen. Förklaringen är att OLR, enligt mitt resonemang ovan, utgår från T^4 medan medeltemperaturen utgår från T. Vissa El Niño/La Niña syns inte alls i OLR-kurvan.
Temperaturförändringar över tropikerna påverkar OLR mest eftersom temperaturen är högre där vilket gör att T^4 varierar mer där än i svalare områden. En ”uppviktning” av temperaturer från varmare områden alltså.