Vi välkommnar Gösta Pettersson åter till bloggen med sitt 7:e gästinlägg

Bild 1. Svante Arrhenius (1859-1927)
1884 utnämndes Svante Arrhenius till (oavlönad) docent vid Uppsala universitet som Sveriges förste företrädare för det nya ämnet fysikalisk kemi. Arrhenius blev också Sveriges första Nobelpristagare när han 1903 tilldelades kemipriset för sin dissociationsteori som lärde oss att salter delas upp i positivt och negativt laddade joner när de löses i vatten.
Klimatologer brukar framhålla att Arrhenius redan 1896 gjorde ett seriöst försök att beräkna styrkan av koldioxidens växthuseffekt. Av mera bestående intresse för klimatologer och naturvetare i allmänhet var dock Arrhenius studier av reaktioners temperaturberoende, vilket han karakteriserade med följande ekvation som bär hans namn:
k = A Exp[-E*/RT] (1)
Arrheniusekvationen beskriver hur hastighetskonstanten (k) för en reaktion beror av den absoluta temperaturen (T).
I detta inlägg ska jag med något annan vinkling än tidigare ta upp vad denna ekvation säger oss om temperaturens inverkan på koldioxidutbytet mellan luft och hav.
Vi vet att kallt vatten löser mer koldioxid än varmt vatten. 1900-talets globala uppvärmning måste därför ha medfört att koldioxid nettomässigt frisatts från oceanerna och överförts till luften. Sådan termisk avgasning har med säkerhet gett ett bidrag till den ökning av luftens koldioxidhalt som uppmätts vid Hawaii sedan 1958 och som grafiskt åskådliggörs av den s. k. Keelingkurvan. Hur ska man kunna skatta hur stort detta termiska bidrag har varit?
För en kinetiker är arbetsgången tämligen given. Först försöker man bilda sig en uppfattning om vad som basalt kännetecknar termisk avgasning. Det sker lämpligen genom att granska kinetiken för ett system bestående enbart av luft och hav
![]() (2)
(2)
där hastighetskonstanten d = d(T) förutsätts vara temperaturberoende enligt Arrheniusekvationen. Enklare än så kan man inte definiera ett system som tar hänsyn till att koldioxidens vattenlöslighet minskar med ökande havstemperatur.
Massverkans lag föreskriver att tidsberoendet för luftkoncentrationen av koldioxid i detta system ges av differentialekvationen
dx/dt = – k x + d(T)y (3)
Derivatan dx/dt står för den hastighet med vilken luftens halt av koldioxid ändras. Jag kommer att kalla den för koldioxidens ändringsfart.
Låt oss nu granska vad som kvalitativt kan utläsas av Ekv. (3). Temperatureffekter på hastighetskonstanter är momentana. En ökning av temperaturen leder enligt Arrheniusekvationen till att d(T) omedelbart ökar i storlek, vilket medför att även ändringsfarten momentant ökar och ger upphov till termisk avgasning. En temperaturminskning leder analogt till att ändringsfarten momentant minskar. Om temperaturen fluktuerar, så kommer ändringsfarten att fluktuera i takt med temperatur-variationerna utan någon som helst tidsmässig eftersläpning.
Nu vet vi att den Södra Oscillationens temperatursvängningar (El Niño vs. La Niña) har globalt genomslag; årsutjämnade globala havsvattentemperaturer uppvisar El Niño-fluktuationer. Därför kan vi på basis av vår kännedom om temperaturberoendet av koldioxidens vattenlöslighet och ovan beskrivna kvalitativa implikationer av Arrheniusekvationen förutsäga att koldioxidens ändringsfart måste uppvisa motsvarande fluktuationer. Har dessa upptäckts vid analyser av Keelingkurvan?
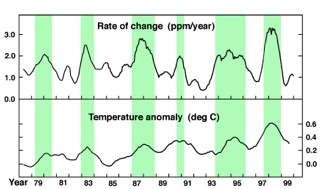
Bild 2. Keelings beskrivning av sambandet mellan temperaturens El Niño-fluktuationer och den atmosfäriska koldioxidhaltens ändringsfart.
Ja, helt visst! Bild 2 visar hur Keeling själv återgett och förtydligat (gröna fält) sambandet mellan temperaturens El Niño-fluktuationer och de observerade fluktuationerna av koldioxidens ändringsfart. Salbys analyser, som granskats och kommenterats i flera SI-inlägg, bekräftar i kvantitativa termer sambandets existens. Det råder inget tvivel om att det föreligger en temperatureffekt på ändringsfarten i den kvalitativt förväntade riktningen och av den förväntade momentana arten.
Vidare kan man notera att det rör sig om en mycket stark effekt. Temperaturhöjningar på mindre än en grad tycks enligt Bild 2 genomsnittligt öka ändringsfarten med en faktor två eller mer. Det kan jämföras med kemisternas tumregel att det vanligen krävs cirka fem graders temperaturökning för att fördubbla reaktionshastigheter. Salby och andra (t. ex. Spencer) har fog för sina slutsatser att El Niño-fluktuationerna av ändringsfarten är av sådan styrka att de torde härröra från en termisk effekt som bör ha gett högst signifikanta bidrag även till Keelingkurvans långsiktiga trend.
Att skatta det termiska bidragets storlek kräver någon form av kvantitativ modellering av de observationer som gjorts. Sådan modellering måste minimalt ta hänsyn till reaktionerna i Ekv. (2) och till den temperaturberoende hastighetskonstanten d(T). Därvidlag blir Arrheniusekvationen åter av intresse, nu som en såväl empiriskt som teoretiskt befäst kvantitativ beskrivning av hastighetskonstanters temperaturberoende.
Arrhenius fann att temperatureffekters styrka bestäms av en parameter (E* i Ekv. 1) som han gav namnet aktiveringsenergi. Storleken av E* har ett direkt inflytande på amplituden av koldioxidens ändringsfarts El Niño-fluktuationer, och kan omvänt skattas genom analys av amplitudernas storlek. I ett tidigare inlägg har jag med utgångspunkt från luft/hav-systemet i Ekv. (2) visat att sådan analys ger skattningen E* = 165 kJ/mol/K om man förutsätter att koldioxidens uppehållstid (dvs. reciproka värdet av hastighetskonstanten k) är 14 år. I ett efterföljande inlägg påpekade jag att man faktiskt inte behöver förutsätta något om uppehållstidens storlek. Keelingkurvan med dess El Niño-fluktuationer innehåller tillräckligt med information för att medge skattning av såväl uppehållstiden som aktiveringsenergin.
Paper 4 ger en reviderad version av min tidigare redovisade analys av temperatureffekterna på luftens koldioxidhalt. Revisionen har tillfört nya detaljer om analysförfarandet, men slutsatserna är de samma som tidigare (illustrerade av Bild 3): Såväl Keelingkurvans El Niño-fluktuationer som dess långsiktiga trend kan kvantitativt återges av luft/hav-modellen i Ekv. (2) för i förra stycket angivna parametervärden, vid beräkningar baserade på föreliggande data om temperaturvariationer och antropogena koldioxidutsläpp. Den erhållna skattningen E* = 165 kJ/mol/grad svarar ungefär mot att en grads temperaturökning på sikt frisätter 60 ppm koldioxid. Det är en temperatureffekt av sådan styrka att den bör ha bidragit till ungefär hälften av 1900-talets observerade ökning av luftens koldioxidhalt.
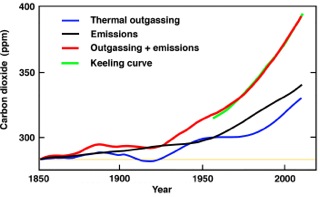
Bild 3. Modellberäkningar av bidragen från antropogena utsläpp och termisk avgasning till luftens ökade koldioxidhalt, jämförda med de direkt uppmätta halterna (Keelingkurvan, grön)
Tyvärr är den mänskliga hjärnan inte så funtad att den intuitivt förmår integrera Ekv. (3), speciellt inte när ekvationen innefattar en temperaturberoende term och dessutom måste kompletteras med en term svarande mot de antropogena utsläppen. Resultaten i Bild 3 föreskrivs med matematisk stringens av den kinetiska differentialekvation de baseras på, men är omöjliga att komma fram utan att numeriskt lösa ekvationen. Det är med andra ord svårt att intuitivt inse eller känna sig övertygad om att Keelingkurvan t. ex. svarar mot uppehållstiden 14 år.
Det är därför jag har dragit uppmärksamhet till ”bombkurvan”, den som beskriver hur snabbt det genom kärnvapentesten producerade överskottet av C14-koldioxid försvunnit ur luften efter det att provstoppsavtalen trädde i kraft. Bombkurvan ger nämligen en direkt och därmed lättförståelig bild av tidsförloppet för överföringen av ett luftöverskott av C14-koldioxid till naturen i övrigt.
Paper 5 redovisar en strikt kinetisk analys av bombkurvan, så som den ter sig (Bild 4) efter det att jag korrigerat mitt ursprungliga misstag rörande översättningen av uppmätta ∆C14-data till värden som svarar mot mängden C14. Kontentan av analysen är att Ekv. (3) för det enkla luft/hav-systemet i Ekv. (2) ger en nära nog perfekt beskrivning av bombkurvan för statistiskt sett samma parametervärden som de som gav en nära nog perfekt beskrivning av Keelingkurvan. Det finns alltså ingen som helst anledning att betvivla att bombkurvan är representativ för vad som enligt Keelingkurvan händer med kontinuerligt tillförda pulser av antropogena koldioxidutsläpp.
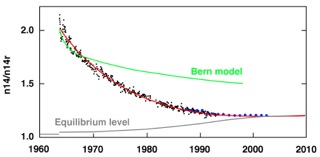
Bild 4. Bombkurvan (svarta mätpunkter) beskrivs förträffligt (röd kurva) av Ekv. (3) och är oförenlig med Bernmodellens beskrivning (grön kurva) av relaxationen av överskottspulser av koldioxid
Bombkurvan ger därför direkt belägg för att relaxationen (jämviktsinställningen) av atmosfäriska överskottspulser av koldioxid följer ett monofasiskt förlopp som styrs av uppehållstiden 14 år och som därmed är väsentligen fullbordat inom loppet av några decennier. Observationerna i Bild 4 ger inget stöd åt kolcykelmodeller (t. ex. Bernmodellen) som föreskriver att relaxationsförloppet är utpräglat flerfasiskt och inte närmar sig jämvikt förrän efter hundratals eller tusentals år.
Och för att återvända till huvudtemat i detta inlägg: Bombkurvan ger även direkt belägg för att jämviktsläget för relaxationen har påverkats av temperaturen i den riktning och den utsträckning som Arrheniusekvationen anger (grå kurva i Bild 4).
Vad har då FN:s klimatpanel (IPCC) att säga om de ovan beskrivna temperatureffekterna? Inte mycket. Bombkurvan har man aldrig behagat visa eller analysera. Den senaste IPCC-rapporten redovisar fluktuationerna i koldioxidens ändringsfart (AR5, WG1, Fig. 6.12) med kommentaren att det finns skäl att tro att de genereras av source/sink-processer, vilket är en intetsägande självklarhet. Man nämner att den mest iögonenfallande ändringsfartstoppen sammanfaller med El Niño-perioden 1997–98 och påpekar att den har sitt ursprung i tropiska latituder. Det är svårt att veta vad man vill ha sagt med det, eftersom hänvisning ges till en rapportsektion (6.3.6.3) som är obefintlig.
Desto uppenbarare är det vad IPCC sorgfälligt undviker att säga och visa. Inte ett ord om att El Niño-året 1998 var osedvanligt varmt. Inte ett ord om att ändringsfartens toppar genomgående sammanfaller med El Niño-periodernas globala temperaturtoppar. Inget diagram som belyser detta, trots att korrelationen dokumenterats och betonats av Keeling själv (Bild 2), och av flera forskare anförts som belägg för att termisk avgasning signifikant bidragit till den långsiktiga ökningen av luftens koldioxidhalt.
Och det är naturligtvis där skon klämmer. IPCC har i samtliga rapporter byggd sin argumentation på den förutfattade meningen att de ökande lufthalterna av koldioxid så gott som uteslutande orsakats av våra utsläpp av antropogen koldioxid. Samtliga IPCC-stödda kolcykelmodeller, och därmed alla IPCC-stödda klimatmodellers spådomar, baseras på denna ostyrkta förutsättning. Det är förståeligt att IPCC undviker att informera om och analysera observationer som gör det befogat att ifrågasätta förutsättningens giltighet.
Det är därför jag har funnit det angeläget att påvisa hur svaga grunder IPCC bygger sina bedömningar på i detta avseende. Utsläppen av antropogen koldioxid har med säkerhet bidragit till att öka luftens koldioxidhalt, men det har även termisk avgasning med säkerhet gjort på grund av 1900-talets globala uppvärmning. I en sådan situation med två säkerställda bidragskällor kan man inte göra några vetenskapliga framsteg på basis av förutfattade meningar, utan är tvungen att söka skatta respektive bidrags storlek från föreliggande empiriska data.
Då kan man notera att en uppsjö av experimentella mätningar med olika metoder samstämmigt har visat att koldioxidens uppehållstid är i storleksordningen 5–15 år, vilket sedan länge anförts som det starkaste argumentet mot att antropogena utsläpp har varit den huvudsakliga källan till de stigande koldioxidnivåerna. Analyserna i Paper 4–5 befäster detta motarguments giltighet med sina belägg för att Keelingkurvan, dess El Niño-fluktuationer och bombkurvan alla svarar mot uppehållstiden 14 år, samt för att termisk avgasning enligt Arrheniusekvationen varit en ungefär lika betydelsefull källa som utsläppen.
Vilka slutsatser det är rimligt att dra från dessa resultat har berörts i tidigare SI-inlägg och framgår även av diskussionerna i Paper 4–5. Den väsentligaste slutsatsen jag själv drar är att man inte kan lita på klimatprojektioner som räknats fram med hjälp av modeller som negligerar den termiska agasningen. Sådana klimatförutsägelser (vilka är de enda som beaktats av IPCC) tycks överdriva effekterna av antropogena koldioxidutsläpp alltför gravt för att ge någon information av signifikant prognostiskt intresse.
Professor emeritus i Fysikalisk Kemi vid KTH. Klimatdebattör sedan 2003.







OT Enligt Vetenskapsradion så smälter snön på Grönland nu dubbelt så snabbt mot tidigare för att den blivit mörkare.
I here by rest my case!!
Snygg bevisframställan.
SörenG #1
Ja titta, den är ju kolsvart !
http://www.summitcamp.org/status/webcam/
Att snön/isen smälter på ytan sommartid på Grönland kunde de konstatera redan på 1800-talet.
http://runeberg.org/polexp1883/0240.html
http://runeberg.org/polexp1883/
Snygg redovisning som åtminstone för mig fyller ett glapp mellan vad jag intuitivt (dvs. med begränsade teoretiska, men ändå kunskaper) och observation av verkligheten kommit fram till.
Annorlunda uttryckt, visar du tydligt att atmosfärens innehåll av CO2, i synnerhet långsiktigt, styrs av Jordens variationer i temperatur och inte av våra utsläpp. Vad som i verkligheten styr dessa variationer i temperatur vet vi mycket lite om. Men att Solen är faktor värd att beakta står väl klart för de flesta.
Avgasningen pga temperatureffekten kan man lätt notera när man gör kolsyrat vatten.
Kallare vatten innan gasen tillförs ger mer bubblor i vattnet.
På den nivån är mina kunskaper-men det måste väl finnas mängder av kemister som granskat CO2 kurvorna och deras uppbyggnad.
Kan den årstidsvariation som uppmäts vid mätningarna på Mauna Loa vara temperaturberoende?
Jag har sett förklaringar baserade på växtsäsonger!
http://www.woodfortrees.org/plot/esrl-co2/from
Lasse #5 – visst är det så med kolsyra och vatten. För rent vatten kan man lätt kvantifiera effekten i termer av Henry’s lag (det ska vara ca 50 ggr mer CO2 i vattnet än i luften vid jämvikt vid rumstemperatur) – men för havsvatten är det väsentligt mer komplicerat pga karbonatjämvikterna (se Gösta Walins inlägg för några veckor sedan), något som många missar.
http://en.wikipedia.org/wiki/Henry's_law
Visst kan ”årstidsvariationerna” bero på såväl växtlighet som havsupplösning/urgasning.
#5 och #6
Årsvis så följer mätningarna Norra halvklotets växtsäsong eftersom Hawaii ligger på vår sida av Ekvatorn.
http://www.woodfortrees.org/plot/esrl-co2/from:2008/to:2013
Passar på som inloggad.
Grönlands massbalans följs här:
http://www.dmi.dk/groenland/maalinger/indlandsisens-massebalance/
Det är nu isen smälter!
Sot eller sol utreds här.
2012 var extremt.
http://wattsupwiththat.com/2014/06/06/study-greenlands-july-2012-insta-melt-was-triggered-by-a-combination-of-warm-weather-and-carbon-soot/
Att frisättningen av CO2 från haven är starkt beroende av temperaturen T, borde egentligen vara oomtvistat. Ökningen eller minskningen av T, måste naturligtvis ytterst bero på ett över tiden variabelt inflöde av energi från solen. Varifrån annars? Hur skulle landisarna kunna smälta utan en temperaturökning? Frisättandet av CO2 bidrog väl också något till temperaturökningen, men till övervägande del måste frisättningen av vattenångan betytt mer, men klart är att initialt måste värme ha tillförts isen. Man kan se det så här, att den globala temperaturens variabilitet inte kan vara en funktion av CO2, utan det är luftens och havens värme som är styrande, vars värme i sin tur är en funktion av solenergin.
Här kommer en annan syn på CO2 från havet.
http://wattsupwiththat.com/2014/06/09/warming-climates-intensify-greenhouse-gas-given-out-by-oceans/#more-111104
Går de att kombineras?
Ju mer jag lär mig om CO2 desto mer fascinerad blir jag.
Senaste är att det frigörs mer CO2 i kallvatten än varmvatten. Det här är naturlig poesi om jämvikt.
När man ser en planet som jorden och upptäcker det ena eller det andra så blir man häpen av slutresultatet. Betänk dock att det är resultatet av miljontals års av utveckling.
Det är livet som anpassat sig till CO2 inte tvärtom.
Peter Stilbs,
”men för havsvatten är det väsentligt mer komplicerat pga karbonatjämvikterna”
Ja just det! Du kanske skulle nämna det för Gösta…
Om man nu ändå tvunget ska blunda för karbonatjämvikterna… så är Henrys lag ju också temperaturberoende. Och det vore ju nära till hands att använda väl etablerad fysikalisk kemi i sammanhanget istället för att hitta på egna teorier som inte har något som helst stöd varesig i teori, labb eller annat sammanhang.
För att inte nämna ÅTERIGEN att bombkurvan inte säger något om den mycket mer komplicerade frågan om Keelingkurvan.
Jonas B1 #12 – men Göstas resonemang bygger ju på observationer – som är lika sanna, oberoende av vad som finns i ”svarta lådan” bakom. Uppenbart har man urgasning när det blir varmare, även om det nu inte gäller koldioxid i luft/destillerat vatten.
JonasB1 #12
”det vore ju nära till hands att använda väl etablerad fysikalisk kemi i sammanhanget”
Jag förmodar du med ”etablerad” syftar på vad som framkommit vid studier i laboratorieskala. Jag villl minnas att sådana studier (baserade på Henrys lag) visat att 17 ppm CO2 borde frisättas per grads temperaturökning. Det vore dock oklokt att utgå från att detta laboratoriedatum gäller precist för fullskaleobservationer.
Betänk att luftkoldioxid i laboratorieskala jämviktar med vatten inom någon minut. Bland det första klimatpionjärerna på 1940-50 talet med rätta påpekade var att sådana laboratorieresultat INTE kan användas för att beskriva den naturliga jämviktsprocessen, vilken sträcker sig över decennier snarare än minuter. Vill man analysera den naturliga processen måste man i första hand hålla sig till de fullskaleobservationer som gjorts.
”istället för att hitta på egna teorier som inte har något som helst stöd”
De analyser jag redovisat har fullt stöd av elementär reaktionskinetisk teori och praktik.
Revelle använde sig i sitt klassiska arbete (Revelle & Suess, 1957) av samma luft/hav-system och härledde i princip samma differentialekvation (dock att han i avsaknad av datorer betraktade utsläppsfarten som linjär för att kunna lösa ekvationen analytiskt). Revelle fann att uppehållstiden är 10 år, konstaterade att den var för kort för att kunna förklara de stigande CO2-nivåerna, och pekade på möjligheten att även termisk avgasning bidragit som CO2 källa. Hade han fullföljt den senare tanken med att införa Arrheniusekvationen så hade han kommit fram till samma modell som jag.
I stället föredrog Revelle att bortse från temperatureffekten och började laborera med andra tankar (Revellefaktorn). Dessa hans tankar (liksom de som rör karbonatkemin) är långt ifrån invändningsfria, något jag hoppas få möjlighet att belysa i ett senare inlägg.
Det enda ”egna” i min analys är att jag tagit hänsyn till att vi vet att koldioxidens vattenlöslighet är temperaturberoende.
Gösta,
Jag tvekar att återigen ge mig in i en diskussion, men…
Nej, Henrys lag kan inte ensam förklara ALLA fenomen i atmosfären. Men självklart ska du ha med den här där den är fullkomligt central för det fenomen du vill beskriva. Istället för att använda Henrys temperaturberoende hittar du på en egen teori istället för Henrys lag. Så KAN MAN INTE göra vetenskap! Varför skulle inte Henrys lag gälla just i det här fallet? Eftersom du inte gillar svaret? Du måste isåfall först vederlägga Henrys lag. Nån …. ordning måste det ändå vara.
Och då har jag inte ens berört att du helt ignorerar karbonatsystemet, vilket Peter i förbifarten påpekar men inte vill kritisera dig för. Pehr har ju även förtjänstfullt simulerat karbonatsystemet, men den ömsesidiga respekten mellan er är…ska vi säga… en smula överdriven, så han vill inte heller öppet kritisera dig.
Tyvärr, det här är ett par nivåer värre än Michael Mann. Självmål för KU!
GP skriver att utgasning från haven är en viktig CO2-källa. Sanningen är att haven tar upp en hel massa CO2. Det är därför deras pH sjunker.
GP har i sin figur 4 med en grön kurva för Bernmodellen. Detta är dock inte vad denna modell förutsäger.
Detta bara att ta ett par exempel på fel som ältats redan tidigare gånger GP skrivit här. Jonas B1 drar upp några andra.
JonasB1 #15
”Varför skulle inte Henrys lag gälla just i det här fallet?”
Henrys lag är en jämviktslag. Den gäller för system i jämvikt. Den gäller INTE för de observationer som jag har analyserat, vilka avser tidsberoendet av relaxationsprocesser (dvs. system som INTE befinner sig i jämvikt utan strävar mot jämvikt). För sådana system är man hänvisad till en fundamental kinetisk ansats baserad på massverkans lag, så som den i enlighet med elementär kinetisk teori tillämpats av bland andra Revelle och mig.
Thomas P #16 söker åter blanda bort korten. Han tycks vilja få folk att tro att det endast är antropogen CO2 som absorberas i haven (ca 5 GtC per år), när nu naturliga koldioxidupplösningen är ca 100 GtC per år. Det är summan av de två som varierar med temperaturen.
Jag tror nog GP har bättre koll på vad Bernmodellen förutsäger eller inte än TP
Jag stöder helt Gösta Petterssons synsätt här. Vi har att göra med ett mycket komplext system i fråga om om utbytet av koldioxid mellan hav och luft. Göstas modell (GP-modellen) är förmodligen den enklast möjliga beskrivningen av detta komplexa system men beskriver observationerna, både Keelingkurvan och bombkurvan, uppseendeväckande bra. Det är helt logiskt och riktigt att Henrys lag inte kommer in i GP-modellen.
Om man försöker beskriva systemet i detalj med alla reaktioner inklusive hela biosfären i havet så är Henrys lag en av de ekvationer som kommer in. Så har man gjort i kolcykelforskningens avancerade modeller men läsning av IPCC-rapporten måste tolkas som att man misslyckats med de prestationer som GP-modellen har gjort.
Peter #18 Och du skall kalla dig kemist!
Jag talar om *netto* inte specifikt om antropogent kol. Haven absorberar *netto* CO2, dvs de tar upp mer CO2 från atmosfären än de avger till atmosfären. GP talar mycket om hur lösligheten i vatten varierar med temperaturen, men lite om hur den kraftiga höjningen av partialtrycket i atmosfären påverkar jämvikten. Sen blir hans beräkningar närmast meningslösa eftersom de bortser från hela karbonatkemin.
Du må tro att GP har koll på Bernmodellen, men då har du fel. Bombkurvan handlar i huvudsak om hur länge enstaka kolmolekyler stannar i atmosfären medan den ekvation som GP använder sig av handlar om hur CO2-halten svarar på om du släpper ut en mängd CO2 i atmosfären. I och med att systemet är buffrat är det två olika saker och de har helt olika tidsskalor. Detta är välkänt inte bara för fackmän på området utan även för amatörer som jag och om du brytt dig om att läsa tidigare trådar i ämnet här på bloggen för att lära dig något skulle det varit välkänt även för dig.
Det är vidare så att havet tar upp koldioxid i vissa regioner och avger koldioxid i andra. GP-modellens resultat kan tolkas så att antropogen koldioxid tas upp i en större mängd i de upptagande regionerna än enligt IPCC men att naturlig koldioxid avges i de avgasande regionerna i motsvarande högre takt. När temperaturen ökar ökar också hastigheten med vilken denna naturliga avgassning sker.
Pehr #”1 Är haven en nettokälla eller nettosänka för CO2?
Thomas #22,
Den intressanta frågan här är om GP-modellen korrekt beskriver nettoupptaget av koldioxid i havet. Svaret är ja eftersom GP-modellen är anpassad till observerade data för koldioxidhalten i luften och för de antropogena koldioxidemissionerna.
För mig är det tydligt att Göstas värde på koldioxidens uppehållstid atmosfären, ca 14 år, är riktigt, och att IPCC och dess svans som talar om hundratals år har fel. Det är Gösta inte den förste som säger, det var tvärtom vetenskaplig sanning redan för 50 år sedan. Det Gösta däremot gjort med sin 2-boxmodell är att visa hur konsistent detta är med både bombkurvan och Keeling’s resultat. I motsats till IPCC som inte får bokföringen att stämma. Det borde få Thomas P m fl att fundera ett varv till.
Allmänt sett blir inte en sanning sannare för att den publiceras i en granskad tidskrift – men den når flera läsare! Därför hoppas jag verkligen att du gör dig besväret att skicka ditt/dina manus till en sådan tidskrift – och vi håller tummarna för att det blir en hederlig granskning.
/C-G
Lasse #5
”Kan den årstidsvariation som uppmäts vid mätningarna på Mauna Loa vara temperaturberoende?”
Förlåt dröjsmålet, Lasse.
I sommarvärmen glömde jag bort att jag tänkt besvara din fråga men aldrig gjorde det. Förrän nu.
En översiktlig diskussion av Keelingskurvans årstidsvariationer hittar du i http://www.falskt-alarm.se, kapitel 9 avsnitt 9. I efterföljande avsnitt 10 (andra stycket på sid 109) hittar du ett referat av och en referens till Starr’s försök att förklara årstidsvariationerna som temperaturvariationer. Och i mitt inlägg ovan ges en länk till Keelings analys av årstidvariationerna.
Den senare analysen är svårläst och ger inga klara svar. Men den belyser hur svårt det är att tolka årstidsvariationerna på grund av den mångfald av faktorer som måste beaktas (temperatureffekter på koldioxidens vattenlöslighet, temperatureffekter på växtligheten till lands och sjöss, årstidsvariationer av utsläppen av antropogen koldioxid, omblandningen av koldioxid från produktionsställen till mätställen vilken kräver uppåt ett år för att fullbordas).
Dessutom framgår det klart av Keelings data att Keelingkurvans årstidsvariationer måste betraktas som ett lokalt fenomen. Variationerna vid Mauna Loa skiljer sig starkt från de vid Arktis, och är inte ens i fas med de som uppmätts på södra halvklotet.
Huvudparten av dessa komplikationer bortfaller när man håller sig till den årsutjämnade Keelingkurvan och dess El Niño-fluktuationer.
Pekke #5
Att koldioxidhalten sjunker under ”norra halvklotets växtsäsong” är förvisso sant, men det kan också beskrivas som att den sjunker under ”södra halvklotets vinter”. Eftersom södra halvklotet domineras av hav så innebär detta att yttemperaturen över en stor del av havsytan sjunkit, vilket också bör leda till en minskning av koldioxidhalten i atmosfären.
Halvkloten samverkar alltså. Under vår vinter blir södra halvklotets hav varmare medan fotosyntesen på norra halvklotet avtar. Under vår sommar ökar fotosyntesen hos oss samtidigt som södra halvklotets hav blir kallare (och kan ta upp mer koldioxid).
Sten #26 Och så var det det där med hur snabb transporten av luft över ekvatorn är…
Jonas B1 #15,
“Pehr har ju även förtjänstfullt simulerat karbonatsystemet, men den ömsesidiga respekten mellan er är…ska vi säga… en smula överdriven, så han vill inte heller öppet kritisera dig.”
Detta är inget vetenskapligt argument utan är en förmodligen helt felaktig analys av mina och Gösta Petterssons personliga egenskaper. Ett ganska meningslöst argument i det här sammanhanget, anser jag. Varför inte försöka hålla dig till vetenskapen i stället?
Simuleringen av karbonatsystemet gjorde jag med den modell som Bolin och Eriksson (1959) använde. Simuleringarna visar hur Revelleeffekten skulle verka om de antaganden som görs i modellen är riktiga, bland annat att den globala temperaturen inte ändras.
Gösta Pettersson har utformat en annan modell med andra antaganden om karbonatkemin, men helt rimliga antaganden enligt min mening och kan beskriva både Keelingkurvan och bombkurvan även när den globala temperaturen ändras. Modellen stämmer bra med observationerna. Den logiska frågan blir då om Gösta Petterssons modell med sina antaganden om karbonatkemin beskriver observationerna bättre än modeller som bygger på andra antaganden om karbonatkemin?
Den grundläggande skillnaden mellan de två modellerna är att enligt Bolins och Ericssons modell blir karbonajämvikterna begränsande för vad som sker. I Gösta Petterssons modell antas i stället att kolkemin är så komplex i jordsystemet att karbonatjämvikterna inte leder till en sådan begränsning.